Com s’ha comentat a les consideracions generals del sentit, el bloc Visualització i modelització geomètrica ha d’impregnar no només el sentit espacial, sinó tota la resta de sentits que es treballin a l’aula de matemàtiques. Aquesta impregnació ajudarà a la comprensió dels sabers d’altres sentits i alhora enfortirà la base dels continguts geomètrics.
L’ús de models geomètrics, a més d’ajudar tot l’alumnat en la comprensió de conceptes, és la via d’entrada a aquests conceptes per a alguns d’ells. El fet de mostrar un mateix concepte des de diferents punts de vista fa que més alumnes hi puguin accedir. Visualitzar geomètricament propietats aritmètiques o elements algebraics ajuda a fer palpables aquestes idees, i proporciona així una entrada menys abstracta per a una part important de l’alumnat.
Durant el segon curs d’ESO la geometria pren un pes important i és per aquest motiu que aquest bloc de sabers no és gaire extens, però malgrat això es deixa a criteri del professorat (i se l’anima a fer-ho!) el fet de «geometritzar» altres sabers.
Les connexions amb altres sabers són l’essència d’aquest bloc de sabers i és lògic que el bloc de visualització estigui connectat als altres sentits. A causa del pes de la geometria en el curs, la quantitat de sabers d’aquest bloc no és gaire elevada, però tots ells estan connectats a algun bloc de sabers.
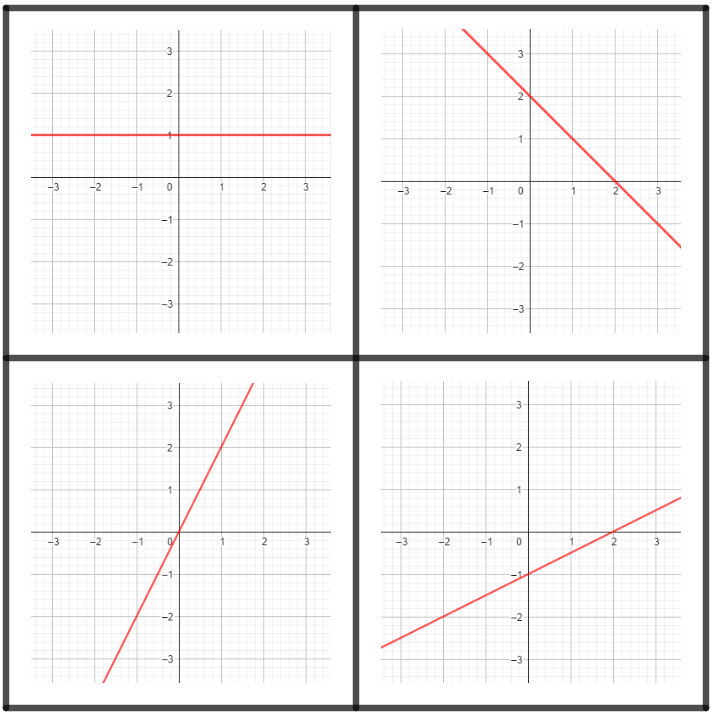
Per a aquest curs també es proposa la introducció a les funcions i el treball amb les funcions constants, lineals i afins. Sembla lògic que l’explicació de l’expressió algebraica d’aquest tipus de funcions ha d’anar acompanyada d’una visualització geomètrica que permeti relacionar cadascuna de les expressions amb un tipus concret de recta i, per tant, la connexió amb #ALG.RF ve donada de forma directa.
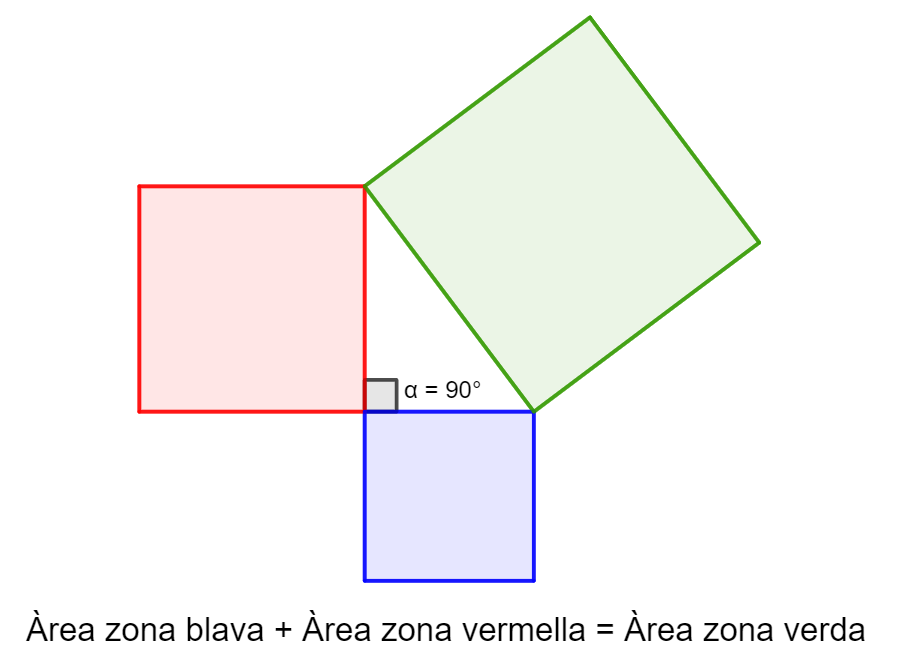
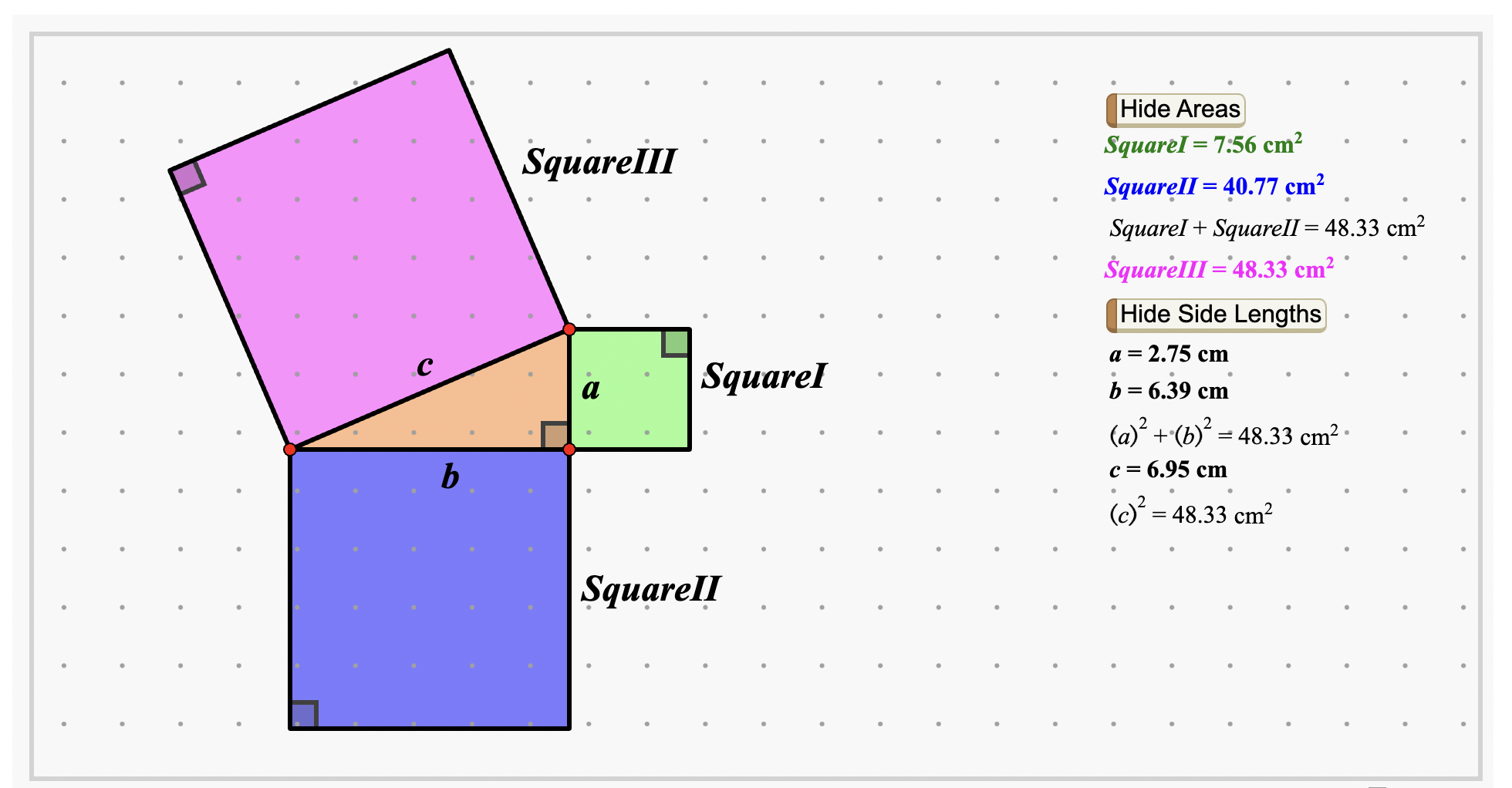
De forma interna dins el sentit espacial, i tal com ja s’ha esmentat en el bloc #ESP.FG, es considera molt important la visualització geomètrica del teorema de Pitàgores. Aquesta visualització no només hauria de ser-hi present durant el descobriment i la demostració del teorema, sinó també, encara que sigui només una visualització mental, sempre que s’utilitzi el teorema. La visualització del teorema de Pitàgores permet fer un treball amb programes de geometria dinàmica i, per tant, també es treballen els sabers del bloc #ALG.PC.
Un dels sabers essencials d’aquest bloc és el saber #2.ESP.VM.C. Aquest es repeteix al llarg de tota l’etapa i sempre s’ha marcat com a essencial perquè, tal com s’ha anat repetint, es considera molt important que es geometritzin tants sabers com sigui possible, siguin del sentit que siguin.
De la resta de sabers, s’ha destacat el #2.ESP.VM.A, perquè es considera essencial tractar les funcions no només des d’un punt de vista algebraic, sinó veient com cadascuna de les expressions correspon a una representació concreta, en aquest cas rectes amb diferents característiques.
El saber #2.ESP.VM.B no s’ha destacat en aquest bloc, no perquè no es consideri important la visualització del teorema de Pitàgores, sinó al contrari, perquè s’ha destacat aquesta rellevància com un saber essencial en el bloc #ALG.FG.
El saber #2.ESP.VM.A pretén que en el moment de treballar les funcions constants, lineals i afins, es visualitzi que aquestes es poden representar per una recta en uns eixos de coordenades. Es considera que aquest treball és molt més ric si es fa en les dues direccions, és a dir, si es treballa la representació d’una determinada expressió i també l’expressió, encara que sigui de forma qualitativa, d’una determinada representació.
Reconeixement i estudi de figures semblants al pla i a l’espai. Raó de semblança.
Comprensió i aplicació del teorema de Tales en diferents contextos. Posició de Tales.
Descoberta, conceptuació i demostració geomètrica del teorema de Pitàgores.
Resolució de problemes que impliquin el teorema de Pitàgores.
Estudi de les propietats i els elements de cossos geomètrics. Classificació de poliedres i cossos rodons.
Estudi i visualització de cossos geomètrics a través dels seus desenvolupaments plans.
Localització en el pla mitjançant coordenades cartesianes. Origen històric.
Visualització de les funcions constant, lineal i afí com una recta amb unes característiques concretes.
Visualització del teorema de Pitàgores com la relació entre les àrees dels quadrats construïts sobre els costats d’un triangle rectangle.
Reconeixement de connexions entre el sentit espacial, la resta de sentits i altres àrees de coneixement properes a l'alumnat.
A continuació, es presenten algunes idees sobre recursos i activitats d’aprenentatge que poden contribuir a l’adquisició dels sabers d’aquest bloc.
Un recurs que pot servir per treballar el saber #2.ESP.VM.A, i molts altres, és el WODB («Which One Doesn’t Belong?», que a vegades es tradueix al català com a «Queli», «quin és l’intrús?»), proposat com a recurs per treballar el saber #2.ESP.CE.J del sentit socioemocional.
En l’activitat es mostra a l’alumnat quatre imatges i es demana quina de les quatre és la intrusa, és a dir, quina no té una característica que tenen les altres tres o, a la inversa, quina és la característica que fa que cadascuna sigui especial. Una vegada mostrades les imatges, cal donar temps als alumnes perquè reflexionin sobre les característiques de cadascuna. Si és la primera vegada que fan l’activitat, és possible que busquin una sola imatge intrusa, però una vegada coneixen el recurs, ja saben que han de buscar les característiques que fan que cadascuna sigui especial. Aquesta activitat potencia molt el raonament i la comunicació d’idees.
Un exemple de Queli podria ser el que es mostra a la imatge següent, però se’n podrien fer moltes de diferents.
També és interessant que sigui el mateix alumnat qui generi aquestes Quelis.
Podem trobar informació interessant sobre les Quelis a la campanya Dimensió web del CREAMAT.
Quan es parla de visualitzar el teorema de Pitàgores, com en el saber #2.ESP.VM.B, el que es pretén és que es dibuixi, encara que sigui de forma mental, la imatge següent:
S’hauria d’aconseguir que aquesta visualització aparegués a les classes de matemàtiques des del moment que s’enuncia el teorema de Pitàgores i que aquesta continués per sempre, fins i tot quan els alumnes ja resolen problemes i situacions que requereixen l’ús del teorema. Que la visualització sigui present no vol dir que els alumnes sempre hagin de dibuixar aquesta representació, que és una opció, sinó que els alumnes, en el seu procés de resolució, l’han de tenir al cap. El moment en què cada persona necessiti deixar de fer el dibuix al paper per passar a fer-lo mentalment és diferent per a totes les persones i no és dolent que, com a professors, es permetin diferències entre l’alumnat.
Per treballar-ho a classe podem fer servir alguna applet, com la que es troba al web Illuminations de l’NCTM, Pythagorean review, en què l’alumnat pot experimentar movent els vèrtexs del triangle rectangle i observant que la relació entre les àrees es manté:
Una altra opció per treballar aquest saber a classe és que siguin els mateixos alumnes els que hagin de fer la construcció amb algun programa de geometria dinàmica. Un exemple de les instruccions que es poden donar a l’alumnat és el següent (sempre que ja tinguin cert domini del programa):
a) Un quadrat el costat del qual sigui la mida d’un dels catets.
b) Un quadrat el costat del qual sigui la mida de l’altre catet.
c) Un quadrat el costat del qual sigui la hipotenusa.
Per treballar el saber #2.ESP.VM.C, reconeixement de connexions entre el sentit espacial, la resta de sentits i altres àrees de coneixement properes a l’alumnat, el professorat ha de plantejar situacions i activitats en què aquest reconeixement sigui possible. Tal com s’exposa a l’apartat «Blocs de competències», dins el punt de connexions amb altres matèries i amb l’entorn, a través del reconeixement, la descripció i la representació de figures planes i tridimensionals, és a dir, a través del coneixement espacial, es pot descriure i interpretar el món on vivim. El treball del sentit espacial a 2n d’ESO ens obre les portes per poder connectar les matemàtiques amb altres matèries i disciplines de maneres molt diverses. El treball dels teoremes de Tales i de Pitàgores ens proporciona contextos històrics on poder establir connexions interessants, i la interpretació de plànols i mapes i la creació de maquetes ens poden ser molt útils a les matèries de tecnologia, física i química, biologia, educació visual o en molts projectes STEAM.
També cal fer notar, com es comenta també a l’apartat «Blocs de competències», dins el punt de connexions amb altres parts de la matemàtica, que el treball de les figures i cossos geomètrics connecta directament amb el sentit de la mesura, donat que ens permet el càlcul de longituds, àrees i volums. Amb el treball de proporcionalitat geomètrica, el sentit espacial connecta amb el sentit numèric, per una banda, però també amb el sentit algebraic. Amb aquest últim sentit, s’estableix una altra connexió forta quan es treballen les coordenades cartesianes, eina fonamental per representar funcions.
Llicenciat sota la Llicència Creative Commons Reconeixement CompartirIgual 4.0