Sabers
- Identificació de casos de proporcionalitat directa a partir de diferents situacions i contextos.
[ESS]#EST.PI#MES.ME
- Ús de les fraccions per treballar problemes de proporcionalitat directa i càlcul de percentatges.
[ESS]#ALG.MM#MES.ME
Orientacions curriculars de matemàtiques de l’ESO
Raonament proporcional
Descripció i orientacions
Reflexions inicials i comentaris sobre els sabers essencials i d᾽ampliació
Aquest bloc vol reflectir les relacions de proporcionalitat entre quantitats en diferents contextos. Això inclou comprendre i aplicar conceptes com la proporcionalitat directa, raons i fraccions, escales, percentatges i les seves aplicacions en situacions de la vida quotidiana.
Mitjançant aquests sabers, els alumnes aprenen a establir connexions lògiques entre les quantitats, utilitzant estratègies com el càlcul mental, la simplificació de relacions i l᾽ús de representacions gràfiques per entendre com les magnituds varien de manera conjunta.
Aquest raonament és essencial per a la resolució de problemes que impliquen el pensament matemàtic i científic, i així fomentar un aprenentatge més profund i aplicat de les matemàtiques.
Comentaris sobre les connexions
Treballant amb taules, gràfiques i expressions algebraiques, l᾽alumnat pot comprendre com identificar la constant de proporcionalitat i aplicar-la a la resolució de problemes reals. A més, aquest coneixement els ajuda a desenvolupar una millor comprensió del concepte de funció lineal, i els prepara per a conceptes més avançats en àlgebra i anàlisi matemàtica.
Observacions sobre alguns sabers específics
El saber #1.NUM.RP.A ha de servir perquè els estudiants aprenguin a identificar les diferents relacions de proporcionalitat segons les diverses situacions quotidianes. És fonamental que siguin capaços de distingir quan una relació és de proporcionalitat directa i quan no ho és. Per aquest motiu, és important plantejar situacions que incloguin proporcionalitat directa, proporcionalitat inversa i relacions no proporcionals.
Una activitat que es pot plantejar a l᾽alumnat és un llistat de magnituds en què hagin de contestar si són o no de proporcionalitat directa. En aquest llistat s᾽ha de posar casos de resposta negativa (quan el cost va per franges, casos de proporcionat afí, algun d᾽inversa, ofertes «en pagues dos, te n᾽emportes tres»).
L᾽alumnat ha d᾽aprendre que la clau és que hi hagi una raó constant (el tant per u) o que observin que hi ha un creixement «paral·lel» de les dues magnituds.
Pel que fa al saber #1.NUM.RP.B, és important treballar problemes en diversos contextos i introduir progressivament tant la proporcionalitat directa com els percentatges. Pot ser convenient introduir el concepte d᾽escala, si bé només fent referència al doble, la meitat… Les escales es treballen més àmpliament a 2n d᾽ESO tant en el sentit numèric com el de la mesura.
Identificació de casos de proporcionalitat directa a partir de diferents situacions i contextos.
Ús de les fraccions per treballar problemes de proporcionalitat directa i càlcul de percentatges.
Recursos i activitats
Recursos i activitats per treballar sabers concrets
A continuació, es presenten algunes idees sobre recursos i activitats d’aprenentatge que poden contribuir a l’adquisició dels sabers d’aquest bloc.
A. Identificació de casos de proporcionalitat directa a partir de diferents situacions i contextos. [ESS] #EST.PI, #MES.ME
Una activitat per treballar els sabers d᾽aquest bloc, sabers #1.NUM.RP.A i #1.NUM.RP.B, seria Nana᾽s Paint Mixup, del professor Dan Meyer. Pot ser un problema per introduir el concepte de proporcionalitat directa.
Aquest és un problema en tres actes. Tal com s᾽explica al web del CREAMAT, un «problema en 3 actes» és una proposta original de Dan Mayer i consisteix a dividir una tasca en tres moments:
Acte 1. Es presenta una situació (amb una imatge, un vídeo...) que sorprengui i estimuli l᾽alumnat a fer-se preguntes. En aquesta fase no es donen dades. Només es formulen i trien les preguntes, especialment aquelles que necessitin les matemàtiques per poder respondre-les.
Acte 2. Es planifica la resolució del problema (o problemes). Es trien i cerquen les dades necessàries. En aquest acte es poden proposar altres imatges o vídeos que orientin l᾽estratègia de resolució.
Acte 3. Es dona resposta a la pregunta o preguntes, i es fan preguntes noves si sorgeixen.
El problema a Nana᾽s Paint Mixup, del professor Dan Meyer, es presenta a l᾽alumnat seguint els actes següents:
- Acte 1: Es mostra a l᾽alumnat un vídeo que es troba en el web de l᾽activitat, en el qual es fa una pregunta i l᾽alumnat, sense fer cap càlcul, ha de fer conjectures. El professorat recollirà les aportacions fetes i incentivarà que en facin més, preguntant a l᾽alumnat, per exemple, si és l᾽única possibilitat.
- Acte 2: L᾽alumnat, utilitzant eines matemàtiques, ha de trobar una solució al problema.
- Acte 3: Es mostra la solució visionant el vídeo que es troba en el web de l᾽enunciat. L᾽alumnat explica com són les seves solucions i es proposa que en trobin d᾽altres que no siguin la mateixa del vídeo.
B. Ús de les fraccions per treballar problemes de proporcionalitat directa i càlcul de percentatges. [ESS] #ALG.MM, #MES.ME
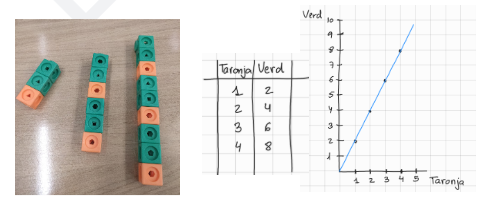
També es pot utilitzar material manipulatiu per treballar aquests sabers, sabers #1.NUM.RP.A i #1.NUM.RP.B. L᾽alumnat pot explorar relacions de proporcionalitat directa apilant blocs de colors segons una constant de proporcionalitat. Per exemple, si la constant de proporcionalitat és 2, per cada bloc de color taronja n᾽hi ha dos de verds. A partir d᾽això, poden construir estructures augmentant progressivament el nombre de blocs de cada color i recollir les dades en una taula. Amb aquestes dades, es pot representar gràficament la relació, assignant un eix a cada color.
Llicenciat sota la Llicència Creative Commons Reconeixement CompartirIgual 4.0