Sabers
- Variables que intervenen en la definició del terme general d'una successió.
#ALG.PA#ALG.RF
- Variables estadístiques discretes i continues.
#EST.DI#EST.IN
A 1r i 2n d’ESO, ja s’ha introduït el concepte de variable i, en particular, a 2n es va vincular amb les relacions funcionals, una idea molt potent que es mantindrà al llarg de tots els estudis matemàtics posteriors. A 3r, es proposa ampliar aquest concepte, relacionant-lo també amb el terme general de les successions numèriques. Es tracta d’una relació natural basada en el fet que una successió és una funció que associa a cada nombre natural 𝑛 un nombre real definit pel terme general an. Així, la connexió entre successions i funcions reforça la comprensió del concepte de variable tant en el context de les funcions com en el terme general de les successions.
Les variables estadístiques també s’han anat introduint de manera progressiva durant els dos primers cursos d’ESO (qualitatives nominals, qualitatives ordinals, quantitatives discretes). Ara, a 3r, es farà un pas més amb el treball de les variables estadístiques quantitatives contínues i les particularitats associades.
Els sabers del bloc Variable tenen un caràcter molt conceptual i adquireixen tot el significat quan es posen en pràctica en el treball dins d’altres contextos matemàtics (funcions, equacions, estudis estadístics). Pel que fa als dos sabers proposats per a 3r d’ESO, s’observen les connexions següents: el saber #3.ALG.VA.A, referent al terme general d’una successió, està estretament vinculat als blocs de patrons i de relacions i funcions del sentit algebraic ( #3.ALG.PA, #3.ALG.RF); i el saber #3.ALG.VA.B, per la seva naturalesa, està connectat amb els blocs de distribució i inferència del sentit estocàstic ( #3.EST.DI, #3.EST.IN).
En cursos anteriors, fins i tot a primària, l’alumnat ja ha treballat amb seqüències numèriques i la descoberta de patrons senzills. Ara es fa un pas més establint el terme general d’una successió com a expressió del patró que permet calcular tots els termes. És clau donar significat a la notació dels termes a1, a2, a3, a4…, i distingir entre les dues variables presents: el valor del terme i la posició, indicada pel subíndex. Consolidar aquesta idea ajudarà a fer un pas més cap a l’abstracció i la introducció de la notació an per representar el terme situat a la posició 𝑛, que s’anomena terme general.
Quan la successió té un patró de construcció (no totes les successions numèriques el tenen), el terme general pot estar definit a través d’una expressió algebraica que dona el valor d’an a partir de la seva posició 𝑛 (per exemple, an = 5𝑛 + 3, an = 2n) o a partir dels termes anteriors de la successió, de manera recurrent (per exemple, an + 2 = an + 1 + an , amb a1 = 1 i a2 = 1, que seria el cas de la successió de Fibonacci).
Caldrà saber calcular els termes de la successió coneixent el terme general i, quan sigui possible, esbrinar el terme general coneixent alguns termes de la successió. Entendre bé aquesta relació entre posició i valor del terme consolida la idea que tota successió és una funció que assigna a cada nombre natural 𝑛 un nombre real an, la qual cosa justifica la connexió amb el bloc de relacions i funcions dins del sentit algebraic. També es pot introduir la notació de la successió tant en format {a1, a2, a3, a4…} com en format {an}, donant-hi sentit.
La novetat a 3r és la introducció de les variables estadístiques quantitatives contínues, que són aquelles que poden adquirir qualsevol valor dins d’un interval. Això vol dir que poden assolir un nombre infinit de valors dins d’un rang, de manera que, entre dos valors possibles, sempre n’hi pot haver d’altres. És important consolidar aquesta idea per mitjà d’exemples que facin notar la diferència respecte a les variables quantitatives discretes. El tractament de variables quantitatives contínues comportarà particularitats importants en l’anàlisi estadística (com la necessitat d’agrupar-les en intervals, classes) així com en la representació.
Variables que intervenen en la definició del terme general d'una successió.
Variables estadístiques discretes i continues.
A continuació, es presenten algunes idees sobre recursos i activitats d’aprenentatge que poden contribuir a l’adquisició dels sabers d’aquest bloc.
Els recursos següents poden ajudar a comprendre la relació entre la posició 𝑛 i el valor an.
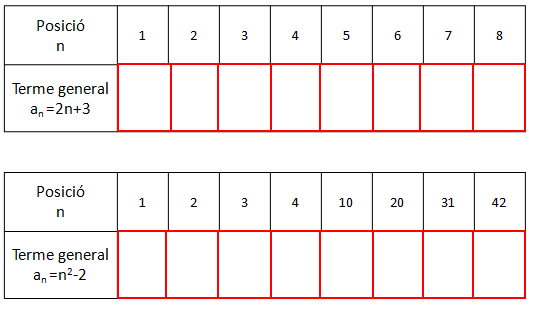
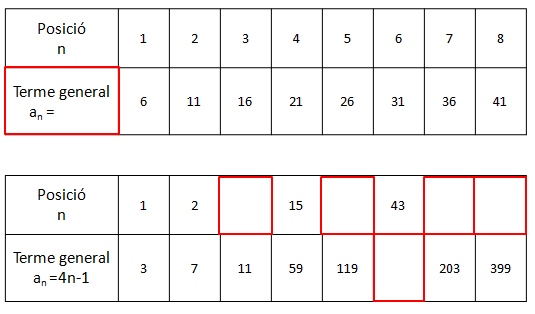
Es poden fer exercicis de pràctica productiva, com ara calcular alguns termes de la successió a partir del terme general, esbrinar el terme general a partir d’alguns termes de la successió, o calcular la posició d’un terme conegut el seu valor i el terme general de la successió. Particularitzant una idea del professor Sergi del Moral, es poden utilitzar taules del tipus següent, en què l’objectiu és omplir les caselles en blanc (pot ser molt útil projectar-ho i fer-ho de manera col·laborativa amb tota la classe) fent servir notes adhesives.
La pàgina web de Visual Patterns és altament recomanable per treballar l’obtenció de termes generals de successions que expressen el nombre d’objectes que componen cada imatge en una seqüència d’imatges que segueixen un patró constructiu. En concret, es pregunta quants objectes componen la figura 43 de la seqüència. Aquest tipus d’activitats és excel·lent per treballar la visió geomètrica, el raonament, les expressions algebraiques i les variables que intervenen en la definició del terme general d’una successió.
Els fulls de càlcul són un bon recurs per visualitzar les variables que intervenen en una successió: la posició i el valor del terme. També permeten construir la successió a partir del terme general, que s’introdueix com a fórmula de càlcul, o generar successions recurrents.
En situacions contextualitzades, la posició i el terme general tenen un significat concret. Per exemple, en el camp de l’educació financera, es pot plantejar un problema com el següent, en què la posició 𝑛 són els anys i el terme an és el capital acumulat passats 𝑛 anys. En aquest cas, la successió és un model de l’evolució d’un capital:
Suposem que dipositem en un banc un capital de 100 €. El banc es compromet a augmentar aquest capital un 5 % cada any, de manera que els interessos s’acumularan al capital. Quants diners tindrem al final del primer any? I al final del segon any? I al final del tercer any? I al cap de 10 anys? Podríem expressar quin seria el capital al cap d’𝑛 anys? Es podria estudiar l’evolució del capital mitjançant un full de càlcul?
Els següents recursos poden ajudar a treballar les variables estadístiques quantitatives discretes i contínues.
Fer una pluja d’idees amb exemples de variables estadístiques quantitatives, classificar-les com a discretes o contínues, i argumentar-ne l’elecció. El professorat pot suggerir exemples com la longitud del peu, el número de sabata, el temps invertit per diversos ciclistes en una etapa, l’edat, les temperatures, el nombre de mascotes en una casa, etc.
Recollir gràfics estadístics de mitjans escrits i, com a primer pas per interpretar-los, identificar el tipus de variable estadística que s’està estudiant.
Elaborar estudis estadístics per equips d’alumnes a partir d’enquestes aplicades a l’alumnat del centre en les quals es pregunti per variables quantitatives discretes i contínues. Es poden utilitzar formularis en línia o portar diferent material a l’aula perquè ’representin creativament les dades que vagin recollint (policubs, cartes, mongetes, fitxes del parxís, etc.), com mostra la fotografia.

Llicenciat sota la Llicència Creative Commons Reconeixement CompartirIgual 4.0