Sabers
- Resolució de problemes basats en recomptes sistemàtics, organitzant i representant dades mitjançant tècniques visuals i gràfiques.
#ALG.PC
Orientacions curriculars de matemàtiques de l’ESO
Comptatge
Descripció i orientacions
Reflexions inicials
El comptatge és una habilitat matemàtica bàsica i necessària per construir una base sòlida en l᾽aprenentatge matemàtic.
A més, el comptatge fomenta el desenvolupament del pensament lògic i crític. Els alumnes aprenen a analitzar situacions, identificar patrons i fer estimacions, habilitats que són molt útils en situacions quotidianes. També contribueix a desenvolupar la precisió i la capacitat de valorar el grau de rigor necessari en funció de cada context.
En els darrers cursos de primària, els alumnes han començat a treballar amb estratègies diverses de comptatge i recompte sistemàtic, com ara l᾽ús de taules de doble entrada i diagrames d᾽arbre. A 1r d᾽ESO proposem reforçar aquestes estratègies i començar a ampliar-les. El plantejament i la resolució de problemes constitueixen un recurs excel·lent per treballar aquest bloc de contingut.
Comentaris sobre les connexions
El recompte sistemàtic i la representació visual de dades són eines clau en el desenvolupament del pensament computacional, ja que permeten organitzar la informació de manera estructurada, identificar patrons i establir connexions. Mitjançant tècniques com taules, diagrames o gràfics, l᾽alumnat pot analitzar problemes complexos, descompondre᾽ls en parts més manejables i aplicar algorismes per trobar solucions eficients. Aquest procés no només fomenta la comprensió profunda de les dades, sinó també habilitats essencials com la planificació, la seqüenciació i el raonament lògic.
Observacions sobre alguns sabers específics
És aconsellable que les activitats per treballar aquest saber es facin en grups, per tal de fomentar el treball en equip i la comunicació. D᾽aquesta manera, l᾽alumnat aprèn a explicar els seus raonaments i a discutir diferents enfocaments per a un mateix problema. Per tal que aquestes representacions siguin riques i significatives, cal proporcionar diversitat d᾽eines, com ara llapis i paper, material manipulatiu i recursos digitals.
Recursos i activitats
Recursos i activitats per treballar sabers concrets
A continuació, es presenten algunes idees sobre recursos i activitats d’aprenentatge que poden contribuir a l’adquisició dels sabers d’aquest bloc.
A. Resolució de problemes basats en recomptes sistemàtics, organitzant i representant dades mitjançant tècniques visuals i gràfiques. #ALG.PC
Recull del Fem Matemàtiques
Una bona eina per treballar aquest saber és la resolució de problemes que permetin aplicar diferents estratègies per fer un recompte concret i assequible per a tot l᾽alumnat, utilitzant diversos materials manipulatius. Al llarg del procés, i mitjançant preguntes guiades, es pot orientar l᾽alumnat cap a la generalització de la situació o la generació de noves estratègies de resolució.
Els problemes del concurs Fem Matemàtiques són un bon recurs per plantejar a l᾽alumnat. Es tracta de problemes oberts que requereixen una investigació i activen tots els processos matemàtics alhora que treballen la gestió socioemocional. Al web del recull de problemes del FM hi ha nombrosos exemples en què cal aplicar diferents tècniques de comptatge per arribar a la resposta. En el Fem Matemàtiques 2024 trobem dos exemples destacats: Les piràmide d᾽Al·laia i Fent torres amb peces del Jenga, dues activitats molt pautades i fàcilment transferibles a l᾽aula.
LES PIRÀMIDES D᾽AL·LAIA:
Fa molt de temps, a l᾽antic Egipte, hi vivia l᾽Al·laia, una noieta de 12 anys que somiava construir piràmides per honorar la seva emperadriu Nefertiti i el déu Osiris.
PIRÀMIDES DE BASE QUADRADA:
Al començament sempre pensava en piràmides quadrades i ho feia amb peces de construcció que representava en un rotllo de pergamí amb tota mena de càlculs i dibuixos.
Fixeu-vos en el disseny de la piràmide de base quadrada de costat 4:
- Construïu les piràmides de base quadrada de costat 1, 2, 3 i 4 (podeu ajudar-vos amb cubs encaixables, daus…). Què observeu?
- Quants blocs de pedra caldrà per fer una piràmide de base quadrada de costat 10? Quants nivells té aquesta piràmide?
- Quina és la diferència de blocs de pedra que hi ha entre dos nivells consecutius d᾽una piràmide qualsevol?
- Fa temps va calcular que en una piràmide quadrada molt grossa, la base tenia 99 blocs cúbics més dels que hi havia al segon nivell. Quants blocs cúbics hi havia a la base d᾽aquella piràmide? Quants nivells tindria aquella gran piràmide?
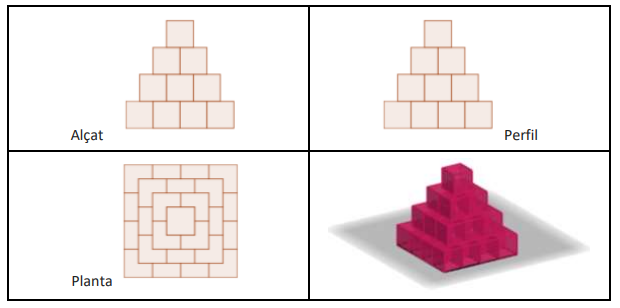
PIRÀMIDES DE BASE RECTANGULAR:
Més endavant, l᾽Al·laia es va adonar que no només hi havia piràmides quadrades. Fixeu-vos en el disseny de la piràmide rectangular de base 3x5 que es mostra a continuació:
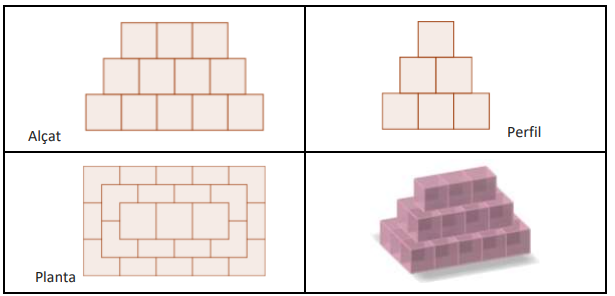
Font: Web del recull de problemes del FM Estudiem ara diferents piràmides de base rectangular.
- Si es disposa de 64 blocs cúbics a la base, quines piràmides diferents podria fer? Ho podeu demostrar? Quants cubs i nivells tenen aquestes piràmides? Què hi observeu?
- Quantes piràmides de base rectangular podeu fer amb 90 blocs (utilitzant-los tots)? Indiqueu els blocs que té la base i els pisos de cadascuna d᾽aquestes piràmides.
- Expliqueu com ha de ser la base d᾽una piràmide per aconseguir que al nivell superior només hi hagi 2 blocs. Hi ha més d᾽una opció? Hi ha alguna relació entre les diferents opcions?
Comptatge visual
Les activitats de «comptatge visual», en què l᾽alumnat només pot observar una imatge durant uns segons sense temps per comptar objectes un a un, ofereixen una bona oportunitat perquè l᾽alumnat comparteixi com visualitza els nombres i els seus mètodes de comptatge, i així fomentar habilitats analítiques i de col·laboració. Aquestes activitats permeten identificar patrons a les imatges i fer estimacions precises. A més, ofereixen un «sostre alt», ja que permeten a cada alumne explorar diferents enfocaments. Escoltar els raonaments dels companys i companyes enriqueix les estratègies individuals de comptatge.
Al web de NRICH hi ha dues activitats destacades per treballar aquesta metodologia: How Many? i How would we count?.
En l᾽activitat How Many? es mostra una imatge amb préssecs durant uns segons.
Es pregunta: Quants préssecs hi ha? Com ho sabeu? Sovint, l᾽alumnat identifica 5 files i 4 columnes, i arriben a la conclusió que hi ha 20 préssecs.
En una segona imatge, es presenta una caixa de taronges.
Això provoca respostes més variades, ja que cada alumne detecta patrons diferents per calcular el total.
La tercera imatge presenta una caixa amb 6 safates de gerds.
Aquesta imatge és ideal per estimular l᾽estimació, ja que implica calcular aproximadament quants gerds hi ha a cada safata. Això ofereix a l᾽alumnat l᾽oportunitat d᾽utilitzar estratègies visuals i matemàtiques per fer prediccions basades en l᾽observació.
Si es vol incrementar la complexitat, es poden incloure fraccions mitjançant imatges de fruites tallades en parts.
En l᾽activitat How would we count? es mostra una imatge amb una disposició de punts. L᾽alumnat, després de veure-la, ha de calcular quants punts hi ha i compartir les seves estratègies.
També es poden dissenyar imatges amb punts o objectes disposats de manera variada per estimular el comptatge i la identificació de patrons.
Llicenciat sota la Llicència Creative Commons Reconeixement CompartirIgual 4.0