Reflexions inicials

Aquest bloc de sabers fa referència, d’una banda, tant a la presa de consciència i gestió de les pròpies emocions com al desenvolupament de les habilitats i destreses relacionades amb la intel·ligència emocional i amb les actituds; d’altra banda, fa referència també a la consolidació d’un sistema de creences que cooperi en l’aprenentatge d’altres sabers.

Com s’afirma en el llibre Matemáticas para aprender a pensar el papel de las creencias en la resolución de problemas (Vila & Callejo, 2004), cal tenir en compte que les creences, per si mateixes, són generadores de determinades actituds. Tant les unes com les altres solen originar-se a partir d’intenses experiències personals, molt probablement relacionades amb l’entorn escolar, o bé a partir de la convivència o l’exposició a mites o influències de l’entorn social i familiar. Aquest fet dificulta generar o modificar aquestes actituds només mitjançant la motivació o l’exposició dels seus beneficis, o fins i tot amb l’atenció socioemocional dels docents. Pel que fa a la voluntat de modificar creences, una intervenció basada únicament en la informació, per molt ben argumentada que estigui, no sol ser eficient. Les creences estan fortament estructurades en sistemes resistents i, en la majoria dels casos, no es basen en aspectes lògics, cosa que fa encara més complexa la seva modificació de manera aïllada. Tanmateix, el que sí que pot afavorir l’aprenentatge dels sabers socioemocionals són les intervencions globals i a llarg termini. Aquestes han de basar-se en experiències riques, treballades a fons i, sobretot, en vivències significatives que connectin amb els alumnes. És fonamental que els docents es presentin de manera convincent i actuïn de forma coherent amb els valors que volen transmetre respecte de les matemàtiques, perquè els estudiants els percebin com a referents creïbles i influents en el seu aprenentatge.

Tal com s’ha indicat en les consideracions generals, la importància d’aquest bloc de sabers en l’educació matemàtica ja es reconeixia quan en la cinquena conclusió del Congrés Català d’Educació Matemàtica 2016 s’afirmava: «Tant el plantejament com la gestió de les pràctiques educatives han de fer-les motivadores, promoure la interacció i tenir en compte la incidència de les actituds i les emocions».

Els sabers d’aquest bloc de Creences, actituds i emocions s’han estructurat en tres grups entorn de:

• L’aprenentatge matemàtic en general, que comprèn els sabers entre #SOE.CE.A i #SOE.CE.E.
• La resolució de problemes, que comprèn els sabers entre #SOE.CE.F i #SOE.CE.I.
• Els processos matemàtics i la matemàtica en general, que comprèn els sabers entre #SOE.CE.J i #SOE.CE.P.

Cal assenyalar que el saber #SOE.CE.D i el saber #SOE.CE.E tenen un ampli espai de superposició. Hi ha raons que han motivat la seva especificació independent, sense que això impliqui la necessitat de treballar-los de manera separada. D’una banda, el saber #SOE.CE.D se centra en l’apreciació que l’alumne té de si mateix, posant l’atenció en la percepció pròpia de les fortaleses i dificultats en relació amb l’aprenentatge de les matemàtiques; en canvi, el saber #SOE.CE.E inclou la mirada «cap a les altres persones» en aquest mateix context. D’altra banda, el saber #SOE.CE.D posa l’atenció en l’autoconfiança de l’alumnat respecte a l’aprenentatge de les matemàtiques, mentre que el saber #SOE.CE.E aborda explícitament els estereotips i prejudicis, un tema que el currículum destaca de manera especial.

Comentaris sobre les connexions

La naturalesa d’aquests sabers exigeix que es treballin de manera integrada en totes les activitats matemàtiques. Segons el tipus d’activitat, es poden enfocar més directament uns sabers que d’altres, però tots han de ser tinguts en compte. Per aquest motiu, no s’han explicitat enllaços amb sabers concrets d’altres sentits, tot i que en la redacció s’ha procurat destacar processos matemàtics i aspectes específics de la matemàtica.

Comentaris sobre els sabers essencials i d’ampliació

Aquests sabers han de tenir una presència constant al llarg de tots els cursos de l’ESO i requereixen una atenció contínua. Per aquesta raó, no s’han identificat sabers essencials ni d’ampliació.

A. Curiositat i interès envers el coneixement matemàtic.

La curiositat i l’interès de l’alumne per les matemàtiques i les actituds que té en el seu aprenentatge poden estar molt condicionades per les seves vivències escolars anteriors, pels comentaris i les opinions que ha pogut sentir del seu entorn, per estereotips socials… Per això, especialment (però no exclusivament) a 1r d’ESO, curs en què s’incorpora a l’educació secundària, serà important tenir en compte:

• Com es veu, en la seva relació amb les matemàtiques?
• Mostra interès per les matemàtiques? Té curiositat per la matèria?
• Quina concepció té sobre les matemàtiques o l’activitat matemàtica?

Els docents han d’acompanyar de manera propera i atenta cada alumne en el seu trajecte d’aprenentatge matemàtic aportant confiança i serenor, compartint el seu gust per la matemàtica i contribuint a construir una mentalitat de «creixement», en el sentit que descriu Jo Boaler a Mentalidades matemáticas (Boaler, 2020).

És essencial vincular l’aprenentatge amb les idees de repte, intriga i curiositat, ja que aquestes poden esdevenir la base d’una motivació continuada, de l’interès, la necessitat i la capacitat per poder arribar a donar resposta a les qüestions matemàtiques plantejades, sovint en forma de situacions d’aprenentatge.

B. Implicació i iniciativa en activitats matemàtiques, siguin escolars o organitzades per entitats externes.

La implicació de l’alumnat en les activitats matemàtiques és clau per al seu aprenentatge. Un element que propicia aquesta implicació és l’atenció personal i sincera del professorat. Serà interessant crear un ambient d’empatia en el qual l’estudiant se senti a gust, per tal d’afavorir una motivació i participació més grans en les activitats matemàtiques de classe. Algunes accions que hi poden contribuir són saludar els alumnes en les trobades casuals, conèixer-ne alguna circumstància, escoltar i mostrar interès en les seves inquietuds, ajudar si cal… Aquests detalls, per petits que siguin, són rellevants.

Tenir present la idea de repte en la planificació de les situacions d’aprenentatge pot afavorir una implicació més gran de l’alumnat i augmentar el seu interès per involucrar-se en la cerca de solucions. D’una banda, això pot contribuir a mantenir la motivació de l’alumnat per donar resposta als reptes i augmentar progressivament la seva iniciativa, i de l’altra, pot aportar més significativitat als aprenentatges que es van fent.

En les activitats de classe, converses matemàtiques, respostes a preguntes, intervencions espontànies o suggerides…, convé estimular, animar, la participació de tothom i evitar qualsevol tipus de biaix; cal no interrompre ni permetre interrupcions, i acollir i valorar amb cura totes les aportacions. Tant com sigui possible, s’hauria d’intentar que la dinàmica de preguntes i respostes a classe no fos únicament en la direcció professor - alumne, sinó sobretot en direccions diverses entre alumnes. Per això, el docent no s’ha de precipitar en la resposta de preguntes i donar oportunitats de resposta a altres persones, fins i tot a través de preguntes com: «Com ho veieu, això?», «Podríem respondre a aquesta qüestió?» o «Podries exposar-nos els teus arguments?». En tot cas, hauríem d’evitar preguntes amb resposta monosil·làbica. Les preguntes són més interessants si promouen argumentacions, explicacions, descripcions; això enriqueix les interaccions i, per tant, els aprenentatges. Una bona gestió del professorat en aquest aspecte serà clau per estimular i mantenir la implicació i la iniciativa de l’alumnat.

S’hauria de promoure que aquesta implicació s’estengués més enllà de l’àmbit escolar. A Catalunya, el teixit associatiu de matemàtiques és molt ric i divers. Liderat per la Federació d’Entitats per a l’Ensenyament de les Matemàtiques a Catalunya (FEEMCAT) i la Societat Catalana de Matemàtiques (SCM), ofereix una àmplia varietat d’activitats dirigides a estudiants de diferents etapes educatives. Es tracta d’activitats organitzades amb cura que poden ser altament motivadores per a l’alumnat i que estan profundament connectades amb la tasca escolar.

C. Consciència de l’aprenentatge matemàtic que es va fent i de com es va aprenent.

Aquest saber fa referència a la consciència que cada alumne ha de desenvolupar sobre el seu propi procés d’aprenentatge matemàtic. Durant l’educació bàsica, no només es tracta d’aprendre, sinó també d’«aprendre a aprendre». Aquest metaaprenentatge permet a l’alumne identificar i gestionar els seus processos d’aprenentatge matemàtic, comprendre millor els mecanismes personals que hi intervenen, reconèixer els seus punts forts i punts febles, descobrir estratègies efectives, promoure la seva autonomia i afavorir la seva capacitat d’adaptar-se a diferents situacions formatives. Donada la importància d’aquest saber, és recomanable que, després de fer una activitat matemàtica, es convidi l’alumne a reflexionar sobre quines destreses emocionals ha après i com les ha après. L’avaluació també té una funció en aquest sentit. En el llibre Building Thinking Classrooms in Mathematics, Peter Liljedahl (Liljedahl, 2020, cap. 13) afirma:

En els darrers 20 anys, s’ha prestat cada cop més atenció a les pràctiques d’avaluació en què el flux d’informació s’inverteix, passant del professor a l’alumne, amb l’objectiu de proporcionar informació sobre l’aprenentatge

Peter Liljedahl

En referència a aquest doble vessant de l’avaluació, també escriu:

[…] si un professor manté una conversa amb un alumne, aquest professor està recollint informació sobre el que l’alumne entén o no entén i el que pot o no pot fer. Si, durant aquesta conversa, el professor ofereix comentaris sobre el que ha obtingut de la interacció, l’alumne també rep informació sobre la seva pròpia comprensió. En qualsevol dels dos casos, el professor pot utilitzar la informació per orientar el seu ensenyament, i l’alumne pot utilitzar-la per orientar el seu aprenentatge

Peter Liljedahl

D. Autoconfiança en les pròpies possibilitats respecte al treball matemàtic i perseverança i resiliència en el seu aprenentatge.

La confiança en el propi potencial matemàtic, essent conscient de les fortaleses matemàtiques i dels aspectes en què cal millorar, és essencial per estudiar aquesta matèria amb interès i eficàcia. Per contra, la manca d’autoconfiança en matemàtiques sovint precedeix, i a vegades provoca, posteriors obstacles i bloquejos. Serà interessant tenir en compte quines són les pròpies creences de cada alumne sobre les seves «possibilitats» en l’estudi matemàtic i convidar-lo a explicar per què pensa el que pensa respecte de la seva relació amb la nostra matèria.

L’alumnat ha de confiar en les seves capacitats matemàtiques i sentir que el professorat també creu en aquestes capacitats. Un dels factors més poderosos per potenciar l’autoconfiança és la creença del professor o professora en les possibilitats de l’alumnat, i que aquest ho percebi clarament. Per tant, el docent ha de transmetre missatges positius i evitar aquells que siguin limitadors, destacant sempre les qualitats matemàtiques de cada estudiant.

Erica Klarreich, en l’article «Meet the First Woman to Win Math’s Most Prestigious Prize», explicant l’etapa escolar de la gran matemàtica Maryam Mirzakhani, afirma:

Per a la seva consternació, Mirzakhani va obtenir mals resultats a la classe de matemàtiques aquest any. El seu professor de matemàtiques no creia que fos especialment talentosa, cosa que va minar la seva confiança. A aquesta edat, “és molt important allò que els altres veuen en tu”, va dir Mirzakhani. “Vaig perdre el meu interès per les matemàtiques”. Tot i això, l’any següent, Mirzakhani va tenir un professor més encoratjador i el seu rendiment va millorar enormement.

Maryam Mirzakhani

La matemàtica no ha de ser una font d’estrès ni d’ansietat per als alumnes, sinó una oportunitat amable i gratificant de creixement. L’ansietat que pot haver-hi en la classe de matemàtiques pot emergir dient «No puc aprendre així» o la frase demolidora «No serveixo per a les matemàtiques». Aquests comentaris sovint són la punta de l’iceberg de pors i creences que interfereixen negativament en l’aprenentatge i que hem de contribuir a superar. Mai no s’haurien d’arribar a sentir les frases citades, especialment quan les pronuncien alumnes molt joves que haurien de veure totes les portes de la vida obertes davant seu. És important que l’educació matemàtica generi situacions que ajudin a evitar aquest sentiment. Més enllà de l’escola, l’alumnat pot rebre missatges del seu entorn social que normalitzin la idea de «no servir per a les matemàtiques». Sovint, hi ha adults que afirmen: «A mi les matemàtiques mai m’han anat bé, no m’agraden, i tampoc no m’han fet falta». Aquest tipus d’afirmacions, socialment acceptades, poden oferir a l’alumnat un pretext per adoptar la mateixa actitud i a les seves famílies una justificació per acabar acceptant-ho. Precisament, les famílies són importants en les creences de l’alumnat sobre la matemàtica i sobre la seva pròpia capacitat per fer matemàtiques.

En el cas particular de 1r d’ESO, és essencial garantir que la transició de primària a secundària no perjudiqui l’autoconfiança de l’alumnat en les seves habilitats matemàtiques. El pas d’una etapa a l’altra ha de ser fàcil i natural, tenint en compte les diferències en la preparació prèvia, les idees preconcebudes sobre les matemàtiques, les creences sobre les pròpies habilitats, així com les metodologies de treball i els estils escolars als quals cada alumne està acostumat. També és crucial considerar aquest aspecte en la incorporació de l’alumnat nouvingut, que sovint afronta una transició tant escolar com social.

S’ha incorporat a cada curs de l’ESO, dins el bloc de Pensament computacional del sentit algebraic, un saber que destaca la importància de l’autoconfiança, la persistència i l’adaptabilitat en el treball matemàtic, ja que alguns recursos associats a aquest bloc faciliten el desenvolupament de les habilitats esmentades.

E. Convicció que tothom pot reeixir en el treball matemàtic, superant qualsevol idea limitadora, independentment del context sociocultural i personal, i tenint especialment en compte la perspectiva de gènere.

L’alumnat ha de tenir la convicció que tothom, i cadascú en particular, pot reeixir en el treball matemàtic. A vegades, de manera molt subtil i en edats molt primerenques, es van construint creences limitadores sobre les capacitats i els rols socials de les persones. Aquestes creences poden influir en les interaccions que es produeixen durant les activitats matemàtiques escolars. És important que el professorat sigui conscient d’això i, tant de manera implícita com explícita, treballi per desmentir aquestes idees preconcebudes i evitar les actituds que se’n deriven. En aquest sentit, és crucial assegurar una participació activa i equilibrada tant de noies com de nois en les activitats matemàtiques. Serà convenient que es valori el treball, l’esforç i la tenacitat per sobre de la suposada intel·ligència innata, la rapidesa de resposta o la presumpta genialitat. L’objectiu és combinar equitat i excel·lència, augmentant la confiança en les possibilitats matemàtiques de tothom i desmantellant estereotips negatius en benefici de tot l’alumnat, tant de qui es veu afectat negativament per aquests estereotips com de qui, aparentment, en rep els beneficis.

La incorporació de persones nouvingudes en qualsevol moment de l’ESO requereix una atenció especial per garantir una acollida suau i tranquil·la, també en l’àmbit matemàtic. És important tenir en compte la preparació prèvia de cada alumne, el seu estil d’aprenentatge particular i les seves creences personals sobre les matemàtiques. Cal proporcionar els recursos necessaris perquè aquest alumnat també tingui la convicció que pot tenir èxit en el treball matemàtic i superar així qualsevol idea limitadora.

F. Constància en la resolució de problemes, establint i millorant estratègies de manera creativa i flexible, i valorant els resultats en el seu context.

Lluís Santaló afirmava que «Ensenyar matemàtiques ha de ser equivalent a ensenyar a resoldre problemes. Estudiar matemàtiques no ha de ser res més que pensar en la solució de problemes». Poc més es pot dir per posar en relleu el paper de la resolució de problemes en l’educació matemàtica.

No es tracta només d’introduir conceptes matemàtics per tal de resoldre problemes, sinó també d’aprendre matemàtiques a través de la resolució de problemes. Les classes de matemàtiques haurien d’immergir-se en un ambient de resolució de problemes, de fer-se preguntes, cercar respostes i fer descobertes. Entenem per ambient de resolució de problemes a l’aula, en els mateixos termes que va definir-lo Paulo Abrantes (Abrantes, 1996, pàg. 7-18), un clima que hauria d’impregnar totes les activitats. En aquest sentit, s’entén que la resolució de problemes és un context i la classe de matemàtiques és un lloc on totes les propostes són situacions problemàtiques que l’alumnat ha d’explorar i, on sigui possible, han de fer despertar diverses formes de raonament.

George Pólya, en el prefaci de la primera edició del seu llibre Cómo plantear y resolver problemas (Pólya, 1965a), escriu:

Un gran descobriment resol un gran problema, però en la solució de tot problema hi ha un cert descobriment. El problema que es planteja pot ser modest; però si es posa a prova la curiositat que indueix a posar en joc les facultats inventives, si és resolt pels propis mitjans, es pot experimentar l’encant del descobriment i el goig del triomf. […] Per això un professor de matemàtiques té una gran oportunitat. Si dedica el seu temps a exercitar els alumnes en operacions rutinàries, matarà en ells l’interès, impedirà el seu desenvolupament intel·lectual i acabarà desaprofitant la seva oportunitat. Si, per contra, posa a prova la curiositat dels alumnes plantejant-los problemes adequats als seus coneixements i els ajuda a resoldre’ls per mitjà de preguntes estimulants, podrà despertar-los el gust pel pensament independent i oferir-los recursos per desenvolupar-lo.

George Pólya

 En relació amb la resolució de problemes, i en general amb tota l’educació matemàtica, cal citar el Decàleg de George Pólya que s’inclou en l’apartat 14.8 del seu llibre Mathematical discovery: On understanding, learning, and teaching problem solving (Pólya, 1965b). És un compendi de grans idees:

1. Interessa’t per la teva matèria.
2. Coneix la teva matèria.
3. Coneix les diferents maneres d’aprendre. La millor manera d’aprendre qualsevol cosa és descobrir-la per tu mateix.
4. Prova de llegir les cares dels teus alumnes; intenta entreveure les seves expectatives i dificultats; posa’t en el seu lloc.
5. Dona als teus alumnes no només informació, sinó també saber fer, actituds mentals, l’hàbit del treball metòdic.
6. Deixa’ls aprendre a conjecturar.
7. Deixa’ls aprendre a demostrar.
8. Cerca les característiques del problema actual que poden ser útils per resoldre els problemes futurs: intenta evidenciar l’estructura general que hi ha darrere de la situació concreta actual.
9. No desvelis de cop tot el teu secret, deixa que els teus alumnes facin conjectures abans de dir-los-ho. Deixa’ls que ho descobreixin per ells mateixos tant com sigui possible.
10. Suggereix. No ho imposis mai per la força.

L’alumnat tendeix a valorar el que el professorat considera important. Per això, és clau donar importància al procés de resolució d’un problema, no només al resultat final. Cal apreciar el camí recorregut, valorar enfocaments alternatius, encara que no sempre tinguin èxit, i reconèixer que hi ha diverses maneres de resoldre un problema matemàtic. És més enriquidor resoldre un mateix problema de tres maneres diferents que resoldre tres problemes diferents d’una única manera.

El docent ha de valorar en els alumnes l’esforç, la tenacitat, la reflexió meticulosa, l’exploració sistemàtica de possibilitats, el fet que es prenguin riscos en les propostes, que tinguin consciència que hi poden haver dificultats i errades i que han de servir per aprendre més. Cal que els alumnes tinguin clar que qualsevol projecte important que hagi tingut èxit ha requerit molt d’esforç, ha comportat dificultats i errades, però s’ha tirat endavant amb treball i constància. El mite de la idea brillant sense esforç queda desmentit per la realitat. Recordem les paraules de Thomas Edison «No he fracassat. He trobat deu mil maneres de com no fer una bombeta» i de Pablo Picasso «Quan arribi la inspiració, que em trobi treballant».

La flexibilitat i la creativitat són especialment rellevants en el treball matemàtic. Per aquest motiu, en el bloc de Pensament computacional, dins el sentit algebraic, s’ha inclòs en cada curs de l’ESO un saber que les posa en valor. Els recursos que proporciona aquest bloc afavoreixen l’enginy i la versatilitat que es desitja fer aflorar.

G. Consciència que en la resolució d’un problema emergeixen emocions diverses, gratificants o angoixants, la gestió de les quals és rellevant per arribar a la solució.

Els alumnes arriben a l’educació secundària amb un sistema de creences propi sobre les matemàtiques i la resolució de problemes, format principalment a partir de la seva experiència escolar prèvia. Aquestes creences influeixen en les seves actituds i emocions, són aspectes importants que cal tenir en compte. En aquest context, és molt rellevant mencionar el treball recollit en el llibre Matemáticas para aprender a pensar. El papel de las creencias en la resolución de problemas d’Antoni Vila i María Luz Callejo (Vila Corts & Callejo de la Vega, 2004). Aquesta obra aprofundeix en les creences que influeixen o sorgeixen durant la resolució de problemes matemàtics, destacant-ne la rellevància educativa i proposant camins per transformar-les. Fomentant un aprenentatge més reflexiu i integrador, mostra com les matemàtiques poden ajudar l’alumnat a afrontar situacions inèdites, desenvolupar estratègies de pensament, aplicar coneixements en contextos diversos i potenciar el pensament crític.

Per aconseguir un aprenentatge profund de les matemàtiques, és fonamental crear un entorn que fomenti l’esforç i la perseverança en la resolució de problemes quan les solucions no són immediates, així com la capacitat de superar i aprendre de les dificultats. La resolució de problemes no és una tasca freda i deshumanitzada; al contrari, enfrontar-se a un repte activa emocions, i una part de l’èxit en la seva resolució depèn de la capacitat per identificar i gestionar aquestes emocions, de reconèixer i desactivar fonts d’estrès, de mantenir una actitud resilient i proactiva. En la mesura del possible, els alumnes haurien de ser conscients d’aquestes emocions i intentar viure la resolució de problemes matemàtics d’una manera serena, confiada i positiva, per tal de gaudir-ne i desenvolupar tot el seu potencial.

Cada persona té el seu propi ritme, i la pressió del temps en la resolució de problemes pot generar angoixa, reduir l’eficiència, matar la creativitat i fomentar la tendència a aplicar simples receptes. Això pot transmetre a l’alumne la idea que la rapidesa és una part de l’habilitat matemàtica, una creença que interfereix negativament en l’aprenentatge. Jo Boaler, en el seu llibre Mentalidades matemáticas (Boaler, 2020), cita un fragment de l’autobiografia de Laurent Schwartz, Un mathématicien aux prises avec le siècle (Schwartz, 1997), en què, a partir dels seus records escolars, destaca la importància de la reflexió profunda en contraposició a la rapidesa:

Sempre vaig estar molt insegur de la meva capacitat intel·lectual; pensava que era poc intel·ligent. I és cert que era, i encara soc, força lent. Necessito temps per assimilar les coses perquè sempre necessito entendre-les del tot. Cap al final de l’onzè grau (primer de batxillerat) pensava que era ruc. Però no ho vaig dir a ningú. Aquest tema em va tenir preocupat molt de temps.

Continuo sent igual de lent. […] Al final de l’onzè grau vaig adoptar una perspectiva realista de la situació i vaig arribar a la conclusió que la rapidesa no es correlaciona de manera precisa amb la intel·ligència. El que realment importa és comprendre profundament les coses i les relacions que mantenen entre si; en això consisteix la intel·ligència. El fet de ser ràpid o lent no és rellevant, en realitat

Laurent Schwartz

H. Satisfacció per l’èxit en la resolució de reptes matemàtics, interpretant-lo com una oportunitat per generar noves preguntes.

Pere Puig Adam, en el seu article «Decálogo de la Didáctica Matemática Media» (Puig Adam, 1955), fa un compendi de deu bones idees per a l’educació matemàtica, un decàleg que, malgrat haver estat escrit l’any 1955, continua sent totalment vigent. El desè punt d’aquest decàleg aconsella «Procurar a tot alumne èxits que evitin el seu descoratjament». Tothom hauria de tenir oportunitats d’aconseguir èxits en fer matemàtiques, tothom hauria de tenir els seus «moments de glòria» matemàtica. El professor Charlie Gilderdale afirmava que una classe de matemàtiques ha d’estar plena d’oportunitats d’èxit per als alumnes.

És important que l’alumne experimenti la satisfacció de resoldre un problema complex, que vagi més enllà d’un simple exercici, i d’assolir un repte matemàtic que exigeixi un cert esforç. Això aporta motivació i reforça l’autoconfiança en les seves capacitats matemàtiques. Part de la tasca d’ensenyar matemàtiques consisteix a proporcionar a l’alumne problemes que, tot i ser resolubles dins les seves possibilitats, requereixin atenció, dedicació i treball. La resolució de tot bon problema matemàtic actua com una palanca per avançar. D’una banda, pot convidar a formular noves preguntes (intentant millorar l’estratègia de resolució, modificant el context, canviant algunes condicions, establint generalitzacions, cercant relacions amb altres problemes…). D’altra banda, aconseguir resoldre un repte matemàtic genera confiança per afrontar nous desafiaments. Sovint es diu que no hi ha res més motivador que l’èxit. És important que el professorat contribueixi a fomentar l’hàbit de formular-se noves i bones preguntes, i que, al mateix temps, sàpiga aprofitar la motivació que aporta la satisfacció de l’èxit per ajudar l’alumnat a créixer matemàticament.

És molt important la retroacció (feedback) que es doni als alumnes com a valoració o reconeixement de la seva bona tasca. Per a molts alumnes, aquesta retroacció és molt valuosa, ja que expressa la consideració de l’ensenyant envers la feina feta. Tanmateix, cal posar atenció a l’oportunitat, en el moment en què apareix, i al tipus de retroacció que es transmet per tal que tingui efectes positius en la promoció d’una mentalitat de creixement de l’alumne. Convé enfocar-la més en aspectes concrets de la tasca feta que no pas en qualitats generals de la persona i, en tot cas, subratllar més l’esforç i el treball que no pas l’habilitat o el talent natural. Alguns estudis suggereixen que, sovint des d’edats sorprenentment primerenques, s’estableixen falsos estereotips de gènere sobre l’èxit matemàtic en relació amb l’esforç o les capacitats innates. Una retroacció acurada pot ser fonamental per desmentir aquests estereotips i contribuir a destacar que l’èxit en matemàtiques no es basa en el fet de memoritzar regles o en la rapidesa dels càlculs, sinó en comprendre les situacions i donar-hi sentit.

I. Acceptació de l’error en l’aprenentatge de les matemàtiques, veient-lo com una oportunitat per aprendre més, en comptes d’un obstacle.

En una situació d’aprenentatge, l’error ha de ser considerat com un material de construcció, un missatge que indica àrees que cal millorar i una oportunitat per avançar. Això només serà possible si eliminem el caràcter devaluador que, de vegades, acompanya l’error. Serà bo crear un ambient en què l’error no s’entengui com un fracàs, sinó com una invitació a aprendre més. En aquest ambient serà més fàcil proposar idees, sense el bloqueig que suposa la por d’equivocar-se. Alguns alumnes pateixen intensament la por de l’error, del suposat fracàs o el pretès ridícul, i això impedeix o complica molt la seva participació a classe, en intervencions espontànies o requerides, en converses matemàtiques, en sortides a la pissarra, en exposicions de treballs. La mateixa paraula error, a vegades, té connotacions massa absolutes; en alguns casos, podríem emprar termes com errada o equivocació. Si aconseguim alleujar la «gravetat» de l’error, reduirem la pressió sobre els alumnes i estimularem la seva participació en activitats matemàtiques.

Una peça important en la demostració del teorema de Fermat va ser la conjectura de Taniyama-Shimura (actualment coneguda com el teorema de Taniyama-Shimura, ja que ha estat demostrada). Goro Shimura afirmava sobre el seu admirat company Yutaka Taniyama: «[…] tenia el do de cometre molts errors, gairebé sempre en la direcció correcta. L’envejava per això i vaig intentar en va d’imitar-lo, però em va resultar molt difícil cometre bons errors». No es pot ser més clar a l’hora d’expressar una visió constructiva dels errors en el camp matemàtic, una visió que seria bo traslladar també a l’educació matemàtica.

Cal evitar, tant explícitament com implícitament, que l’error adquireixi una càrrega excessiva que pugui minar l’autoconfiança matemàtica de l’alumne i suggerir una disminució de les nostres expectatives en les seves possibilitats matemàtiques. L’error s’ha d’identificar, treballar i corregir, però no hauria d’envair el territori de les emocions negatives ni de les creences de l’alumne. Aquesta situació provoca, massa sovint, que alguns alumnes, inventant-se límits i oblidant que tothom pot progressar en matemàtiques, afirmin «Jo no serveixo per a les matemàtiques» i encara se n’allunyin més.

Cal treballar les errades, parlar-ne, per aprendre’n i construir-hi coneixement. En el llibre El lenguaje de funciones y gráficas (Shell Centre for Mathematical Education, 1990) es diu:

Les nostres investigacions ens porten a afirmar que els estils d’ensenyament que inclouen la discussió amb els alumnes sobre els errors comuns són més efectius que aquells que eviten l’exposició d’errors sempre que sigui possible.

En el bloc de Pensament computacional dins el sentit algebraic, s’ha inclòs un saber que tracta de la gestió constructiva de l’error. Sovint s’utilitza el terme anglès debugging per referir-se al procés de trobar i corregir errors en el codi, una fase clau en el disseny d’algorismes i en la programació. Aquesta fase il·lustra molt bé el valor de les errades com a oportunitats de millora. En relació amb aquesta idea de depuració d’errors i en el marc més general de la resolució de problemes en context, és rellevant citar els sabers que fan referència a la interpretació i validació dels resultats obtinguts i a la recerca d’alternatives en cas que no siguin coherents.

J. Assumpció del fet que el raonament és un component imprescindible en les matemàtiques.

El raonament és consubstancial a la construcció del coneixement matemàtic, ja que li dona solidesa i coherència, i, per tant, ha de ser present també en l’aprenentatge de les matemàtiques. És important que l’alumnat valori l’estructura lògica de les matemàtiques com una de les seves característiques fonamentals i que prengui consciència de la rellevància de l’argumentació en el treball matemàtic.

Cal destacar la naturalesa actitudinal d’aquest saber: l’alumnat ha d’assumir personalment la importància d’argumentar correctament les seves afirmacions, tant en l’àmbit matemàtic com en la seva vida quotidiana. És fonamental que es desenvolupi l’interès per convèncer altres persones a través del raonament lògic, tant els companys i les companyes de classe com el professorat i, en general, les persones del seu entorn. És possible que, com a resultat d’aquest interès per argumentar, l’alumne descobreixi la necessitat de cercar millors estratègies de raonament, justificacions més sòlides i enfocaments argumentals més efectius.

En tots els sentits (numèric, algebraic, espacial, estocàstic, socioemocional i de la mesura) es presentaran oportunitats per treballar el raonament i, per tant, consolidar aquest saber. El raonament serà fonamental per formular i verificar conjectures, per construir, expressar i contrastar argumentacions, per deduir regularitats i per resoldre problemes. Un llibre excel·lent que reflexiona al voltant del raonament matemàtic i dels aspectes emocionals que hi estan implicats és Pensar matemáticamente, de John Mason, Leone Burton i Kaye Stacey (Mason et al., 1989).

En l’ESO es poden fer raonaments de tipus deductiu i inductiu (potser no formalitzat), però el més important és promoure que l’alumne sigui conscient que el raonament és un component essencial en les matemàtiques, molt més que la simple aplicació de regles, fórmules o mètodes. Com afirma Jo Boaler en el capítol 7 de What’s Math Got to Do with It? (Boaler, 2015), els alumnes que entenen les matemàtiques simplement com un conjunt de regles deixen de gaudir d’una part de la seva bellesa i potència, i han d’esforçar-se molt més per avançar en una escala inacabable de procediments. El professorat hauríem d’intentar que aquest no sigui el concepte que transmetem de les matemàtiques.

Pel seu interès educatiu, en un àmbit menys formal, cal citar el que a vegades s’anomena raonament plausible. Tot i que no posseeix la solidesa formal del raonament deductiu o inductiu, aquest tipus de raonament intenta fer evident la propietat que es vol mostrar. Pere Puig Adam, en el seu llibre La Matemática y su enseñanza actual (Puig Adam, 1960), es refereix a aquest tipus de raonament quan escriu:

No sempre una demostració basada en la reducció a veritats anteriors, qualitat característica de les demostracions de l’escola grega, és la que tradueix les essències de la propietat demostrada, ni molt menys la més adequada des d’un punt de vista didàctic. Per als matemàtics orientals, demostrar era reduir a l’evidència directa, la qual percep el nen millor que un encadenament lògic, del qual sovint no veu ni l’abast ni la necessitat.

Pere Puig Adam

Algunes propietats utilitzades en l’educació secundària (com la que expressa la longitud d’una circumferència o l’àrea d’un cercle) estan molt lluny de poder ser demostrades, en l’ESO, de manera rigorosa, però es poden «mostrar» de manera plausible, sovint a través de l’experimentació amb materials.

El raonament plausible té un component socioemocional interessant com a alternativa al raonament clàssic. En aquest tema cal citar el llibre Matemáticas y razonamiento plausible, de George Pólya (Pólya, 1966), en el pròleg del qual afirma:

Tots sabem que les matemàtiques ofereixen una excel·lent oportunitat per aprendre el raonament demostratiu, però jo sostinc també que no hi ha cap matèria en els programes habituals de les escoles que ofereixi una oportunitat semblant per aprendre el raonament plausible. M’adreço a tots els estudiants interessats en matemàtiques de tots els nivells i els dic: “Aprenguem a demostrar, és clar, però aprenguem també a intuir”.

George Pólya

K. Valoració de la importància d’utilitzar correctament les representacions i el llenguatge matemàtic per a una bona comunicació.

El propòsit d’aquest saber és enriquir la comprensió de l’alumne sobre les matemàtiques com a cos de coneixement, destacant la importància de la comunicació i l’atenció a les representacions i a l’ús correcte del llenguatge matemàtic. La comunicació d’idees matemàtiques és clau per compartir, discutir, ajustar i perfeccionar conceptes. A fi que l’alumne reconegui la rellevància de la comunicació en matemàtiques, cal integrar-la, de manera significativa, en les activitats de classe, ja que no només facilita l’organització i l’aprenentatge de les idees, sinó que també és una eina bàsica per al treball en equip. És important que l’alumne valori els avantatges d’una bona comunicació matemàtica, prengui consciència de la importància d’expressar clarament les seves idees i desenvolupi una actitud de voler i necessitar comunicar-se amb claredat i precisió, tant amb els companys i el professorat com amb qualsevol persona fora de l’àmbit escolar a qui transmeti una idea matemàtica.

És crucial aprofitar totes les oportunitats per incentivar que l’alumne expressi idees matemàtiques amb claredat i precisió, i per fomentar el seu interès per comprendre les idees d’altres persones. Això inclou descriure situacions, explicar procediments, justificar raonaments, argumentar estratègies, analitzar gràfics, interpretar diagrames estadístics, debatre dades, presentar conclusions i mantenir converses matemàtiques. Les classes de matemàtiques ofereixen moltes ocasions per a la comunicació, però és important que s’utilitzi un llenguatge adequat. Les idees han de ser presentades de manera clara, precisa i coherent, amb una terminologia matemàtica correcta, incorporant-hi progressivament notacions, símbols, expressions simbòliques, taules, gràfics, diagrames i esquemes.

Maria Antònia Canals, una referent clau de la nostra educació matemàtica, en una entrevista publicada en la revista Biaix proposa un decàleg per a l’ús de materials manipulatius a primària. Moltes de les recomanacions que s’expressen en aquest decàleg són absolutament aplicables a l’educació secundària. Crida l’atenció l’èmfasi que posa en la comunicació de les idees per part de l’alumnat. Les recomanacions 7, 8 i 10 van en aquesta línia. En particular, la 10 fa referència a la introducció del llenguatge matemàtic. A primària, aquest procés és encara incipient, però a secundària adquireix una rellevància creixent amb la incorporació gradual d’elements de llenguatge formal, especialment en el marc del sentit algebraic, com a part d’un camí cap a l’abstracció en el qual cal intentar que ningú no quedi enrere.

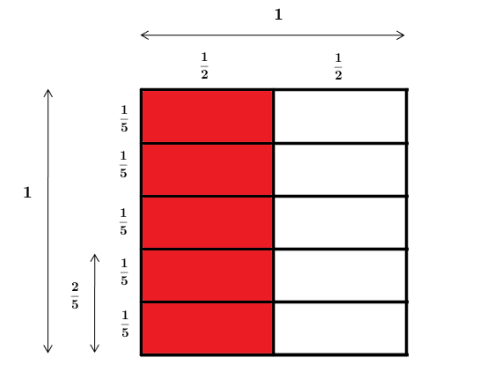
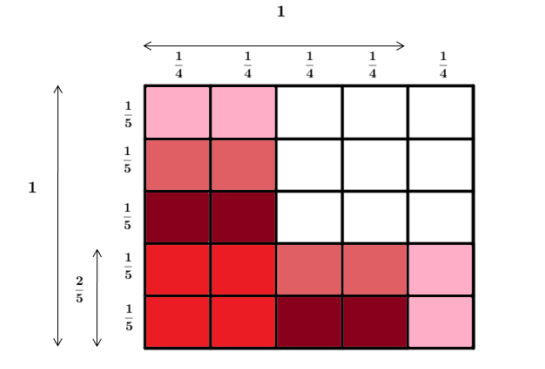
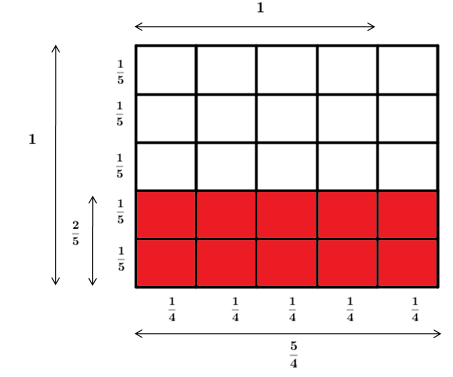
La representació d’idees matemàtiques és crucial en la comunicació. En l’àmbit educatiu, la diversitat de representacions (com ara dibuixos, esquemes, figures geomètriques, construccions amb materials manipulables, taules, gràfics, símbols i recursos TIC) no només ofereix múltiples maneres de presentar idees matemàtiques, sinó que també proporciona diverses aproximacions per comprendre millor aquestes idees. Disposar de múltiples representacions per a un mateix concepte o relació matemàtica permet triar la forma més adequada segons la situació i utilitzar el canvi de representació com a eina estratègica en el treball matemàtic. En l’ESO, les representacions visuals, sovint derivades d’interpretacions geomètriques de conceptes o relacions, seran especialment útils. El seu ús és un aspecte atractiu de les matemàtiques i contribueix significativament a l’assoliment d’aquest saber.

Quan un concepte el podem presentar i treballar a classe representant-lo de formes diverses (materials, escrites, visuals…) estem fent servir el model DUA (disseny universal per a l’aprenentatge), que ofereix un marc de referència per a la creació de contextos d’aprenentatge en els quals es proporcionen múltiples maneres de presentar la informació, de representar-la i de treballar-hi.

L. Interès per establir connexions entre conceptes matemàtics amb altres disciplines i per analitzar i comprendre el món amb una mirada matemàtica.

En aquest saber es preveuen dos tipus de connexions molt diferents:

• Connexions internes, que són les que es produeixen entre idees matemàtiques, proporcionant més significat als conceptes relacionats i aportant solidesa al cos de coneixements matemàtics.
• Connexions externes, que enllacen idees matemàtiques amb altres disciplines o amb l’entorn natural, social o cultural, basant-se en la presència o l’aplicació de les matemàtiques.

Considerant aquests dos tipus de connexions, el saber #SOE.CE.L hauria de contribuir a fer que l’alumnat, en primer lloc, prengués consciència, d’una banda, de la coherència interna de les matemàtiques i de l’encaix perfecte i elegant de les seves peces, i, de l’altra, de la seva importància en altres àmbits. En segon lloc, anant una mica més enllà, que s’interessés per establir i descobrir connexions internes (enllaçant idees matemàtiques) i connexions externes (a partir de la mirada matemàtica al seu entorn).

Les connexions internes són valuoses oportunitats didàctiques que cal aprofitar. En aquest exemple de desenvolupament del currículum es destaquen moltes connexions entre sabers matemàtics. Aquestes connexions conviden a trencar les fronteres dels blocs i sentits per establir enllaços que afegeixen valor a idees aïllades. Hi ha moltes més connexions que les explicitades, i tant docents com alumnes poden identificar enllaços conceptuals en tota la matèria. No s’hauria de presentar la matemàtica reduïda a les parts que la formen. El cos de coneixements matemàtics és més que la suma de les seves parts. Per això, és important reconèixer i tenir en compte les connexions i els processos transversals. Cada connexió interna és una oportunitat educativa que no només reforça els conceptes vinculats, sinó que també transmet la idea que la matemàtica posseeix una forta cohesió interna. Són especialment valuoses les connexions entre sabers no geomètrics (per exemple, dels sentits numèric, algebraic o estocàstic) i l’àmbit de la geometria, ja que en aquests enllaços guanyen ambdues parts: el saber no geomètric guanya valor didàctic a través de la visualització proporcionada per la geometria, mentre que la geometria també hi guanya perquè augmenta la seva presència educativa. Des d’aquesta perspectiva de globalitat, convé fer dues recomanacions:

1. Procurar no compartimentar massa el coneixement matemàtic, transitant sense por a través de les seves connexions internes.
2. Acceptar totes les aproximacions i perspectives d’abordatge a les situacions d’aprenentatge, valorant-les de la mateixa manera i evitant sobrevalorar les que, en aquell moment, encaixen més amb la idea matemàtica que es vol construir. Ben al contrari: aquestes diferents aproximacions poden ser una font de nou treball entre contextos diversos.

Les connexions externes, en canvi, enllacen idees matemàtiques amb altres matèries i amb l’entorn. Sovint, aquestes connexions es basen en la presència de les matemàtiques en aquests àmbits o en la seva aplicació. En particular, les matemàtiques ofereixen tres grans instruments de coneixement i anàlisi: un llenguatge formal, eines de càlcul i manipulació simbòlica, i models matemàtics per analitzar situacions contextualitzades (tractats de manera més concreta en el saber #SOE.CE.M). Aquests vincles són especialment rellevants en les disciplines de l’àmbit STEM. En aquest camp, un llibre molt recomanable és Matemáquinas. La matemática que hay en la tecnologia, de Brian Bolt (Bolt, 1992). El treball a l’aula amb aquest tipus de connexions hauria de projectar la potència de les eines matemàtiques per descriure i analitzar el món que ens envolta, educar la mirada matemàtica i evitar la pregunta «Això per a què serveix?».

Una referència en connexions externes és el llibre Las matemáticas en la vida cotidiana (Garfunkel & Steen, 1999), que presenta aplicacions de les matemàtiques en diversos camps: les votacions electorals, les estadístiques mèdiques, les decoracions en art, les distribucions de mercaderies en ciutats, etc. És a dir, es motiva l’interès de diferents recursos matemàtics (teoria de grafs, estadística, geometria, combinatòria…) plantejant temes de la vida quotidiana.

L’interès per analitzar i comprendre el món des d’una mirada matemàtica ha de vincular-se necessàriament al fet que l’educació matemàtica pot ser una eina poderosa per contribuir a l’assoliment dels objectius de desenvolupament sostenible (ODS), ja que ofereix instruments clau per analitzar, comprendre i resoldre els reptes globals. En particular, cal destacar la importància de la formació estadística, que permet l’anàlisi de dades, la visualització de resultats, la formulació de prediccions i la presa de decisions entorn dels diversos ODS, com ara la Salut i benestar (ODS 3), l’Educació de qualitat (ODS 4), l’Acció climàtica (ODS 13), entre d’altres. L’anàlisi estadística de dades i la matemàtica en general són eines fonamentals per contribuir a la construcció d’un futur més sostenible i just. És important que l’alumnat en prengui consciència.

M. Apreciació de l’interès dels processos de modelització com a forma atractiva d’enllaçar les matemàtiques amb la realitat sobre la qual es vol actuar.

És important que l’alumne, en la seva educació matemàtica, descobreixi i valori l’interès dels processos de modelització com a elements de connexió entre el coneixement matemàtic i la seva aplicació a situacions reals. Quan els estudiants tenen l’oportunitat de veure com, a través del modelatge, les matemàtiques s’apliquen a diferents àmbits, no només augmenta la seva comprensió dels conceptes, sinó també la seva motivació i interès per la matèria.

El pal de paller de la modelització matemàtica és l’aplicació (iterativa) del circuit següent:

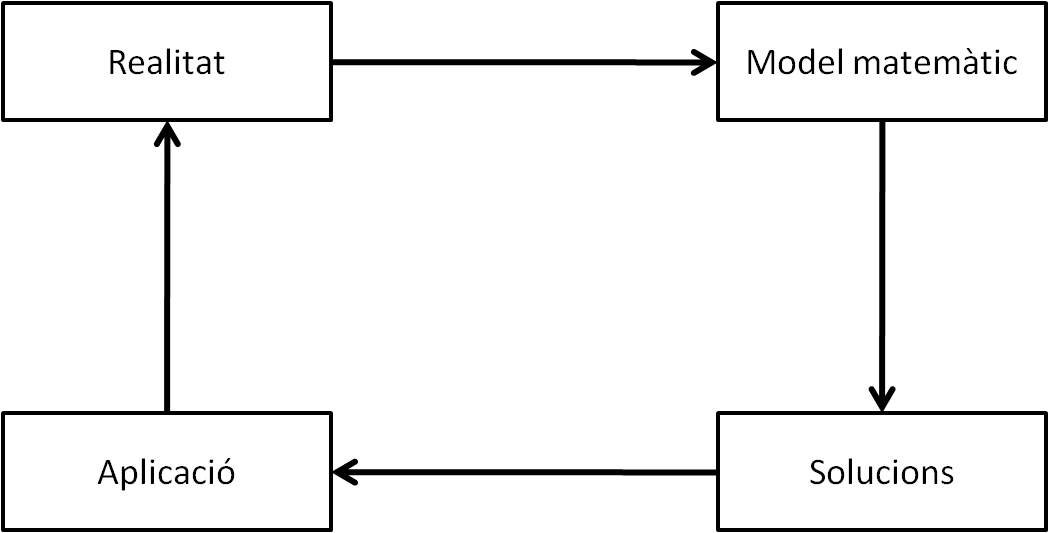
La «realitat» és la vida quotidiana de les persones i depèn de l’edat, dels interessos, de l’entorn social… (esports, alimentació, videojocs, transport escolar, música, rebaixes, màquines, gràfics, disseny, comunicació, salut, viatges, impostos, votacions, hipoteques…). A partir d’ella hom fa o elabora un o diversos models (aproximacions, taules, funcions…). I ja dins el món matemàtic es treballa amb el model inicial (estimar resultats, temptejar noves solucions, calcular…). D’aquest procés, en sortiran unes solucions que aleshores caldrà contrastar amb la realitat tot veient si aporten resultats correctes o bé cal refinar la modelització, començant de nou el cicle.

La llista següent de Henry O. Pollack és una descripció magistral dels passos que cal seguir per modelitzar:

1. S’identifica una cosa en el món real que volem conèixer, fer o entendre. El resultat és una qüestió en el món real.
2. Seleccionem «objectes» que semblen importants en la qüestió del món real i identifiquem les relacions entre ells. El resultat és la identificació de conceptes clau en la situació del món real.
3. Decidim el que considerarem o el que ignorarem sobre els objectes i la seva interrelació. No es pot tenir en compte tot. El resultat és una versió idealitzada de la qüestió original.
4. Traduïm la versió idealitzada a termes matemàtics i obtenim una formulació matematitzada de la qüestió idealitzada. D’això, en diem un model matemàtic.
5. Identifiquem els apartats de la matemàtica que poden ser rellevants per al model i en considerem les possibles contribucions.
6. Fem servir mètodes matemàtics i idees per obtenir resultats. Així sorgeixen tècniques, exemples interessants, solucions, aproximacions, teoremes, algorismes…
7. Prenem tots aquests resultats i els traslladem al principi. Tenim aleshores una teoria sobre la qüestió idealitzada.
8. Ara hem de verificar la realitat. Creiem en el resultat? Els resultats són pràctics, les respostes són raonables i les conseqüències són acceptables?
   1. Si la resposta és sí, hem tingut èxit. Aleshores, el treball següent, que és difícil però extraordinàriament important, és comunicar allò que s’ha trobat als seus usuaris potencials.
   2. Si la resposta és no, tornem a l’inici. Per què els resultats no són pràctics o les respostes no raonables o les conseqüències inacceptables? Segurament, el model no era correcte. Examinem el que hem pogut fer malament i per què, i comencem de nou.

Com fan palesos els passos anteriors de la modelització, aprendre aquest procés exigeix diàleg i interacció, fruir de seleccionar recursos que es coneixen o que cal cercar i que ara cal confrontar amb la realitat. El fet que els alumnes sentin l’interès pels processos de modelització matemàtica contribueix a una experiència d’aprenentatge més completa, tant en l’àmbit cognitiu com emocional.

Naturalment, aquest saber enllaça molt bé amb els sabers del bloc Model matemàtic del sentit algebraic. En concret, en el bloc #1.ALG.MM s’exposa l’esquema de Maas (2006) sobre el procés de modelització, similar al de Pollack exposat aquí, i es comenta que el procés de modelització matemàtica no s’ha de confondre amb l’ús d’un model per representar o resoldre un problema que no requereix tot el procés. És precisament en la primera i la darrera fase (el pas de la situació real al model i viceversa) quan es pot treballar millor l’interès dels processos de modelització com a forma atractiva d’enllaçar les matemàtiques amb la realitat.

N. Gaudi del plaer de resoldre reptes propis de la matemàtica recreativa.

Fer matemàtiques pot ser molt divertit quan es juguen determinats jocs d’estratègia, o es plantegen reptes que cal resoldre amb enginy, o es descobreixen resultats inesperats. Benvinguts i benvingudes a la matemàtica recreativa!

S’atribueix a John Edensor Littlewood la frase: «Un bon passatemps matemàtic val més, aporta més a la matemàtica, que una dotzena d’articles mediocres». L’experiència personal que proposa la matemàtica recreativa té moltes semblances amb el procés d’intentar entendre i resoldre una dificultat matemàtica. La frontera entre la resolució d’un problema matemàtic i l’exploració d’una recreació matemàtica és molt difusa. Un trencaclosques, un enigma, un puzle, un passatemps de matemàtica recreativa pot oferir una gran oportunitat didàctica.

També els jocs de taula són una font magnífica per plantejar problemes. No només els jocs tradicionals, sinó especialment diversos jocs de taula moderns, són situacions que porten de manera natural a formular problemes interessants, tant en els jocs d’estratègia com en els d’atzar. En l’apartat de recursos inclourem algunes activitats per treballar amb jocs a l’aula.

Actualment es disposa d’una magnífica col·lecció de material matemàtic recreatiu fruit de les aportacions de Martin Gardner, Henry Dudeney, Sam Loyd, Miguel de Guzmán, Miquel Capó, Jordi Deulofeu, etc. Pot ser un bon recurs per a l’educació matemàtica.

O. Valoració d’aportacions matemàtiques fetes per persones, dones i homes, en llocs diversos i en diferents moments de la història.

S’atribueix a Isaac Newton la frase: «Si he vist més lluny que no pas els altres, és perquè m’he enfilat damunt les espatlles dels gegants». El coneixement matemàtic ha estat construït gràcies a l’esforç de gegants i de gegantes que han deixat empremta en una cursa de relleus mil·lenària, l’únic premi de la qual és disposar d’una eina poderosa per entendre el món que ens envolta. El saber #SOE.CE.O subratlla la importància que l’alumnat valori les contribucions matemàtiques fetes per aquestes persones, tot apropant-se a la seva trajectòria i al context històric, social i cultural en què van treballar. Aquesta aproximació permet posar de manifest els seus esforços, aportacions, encerts, errades, dificultats i controvèrsies. Humanitzar el coneixement matemàtic escolar és fonamental, ja que ajuda a mostrar que la matemàtica no és només un conjunt de resultats abstractes, sinó del producte de l’esforç de moltes persones.

A vegades, les aproximacions biogràfiques a la història de les matemàtiques s’han centrat predominantment en homes europeus. Sense menystenir el valor d’aquestes aportacions i d’aquests personatges, és crucial adoptar una perspectiva més inclusiva que reconegui també les contribucions de les dones i les aportacions sorgides de cultures diverses. Això inclou:

• En primer lloc, cal destacar les moltes contribucions anònimes que, al llarg de la història i en cultures diverses, han fet persones sàvies, artesanes, inventant eines i recursos de base matemàtica (simbologies numèriques, sistemes de numeració, mesures tradicionals, instruments de dibuix, àbacs, rellotges, calendaris, construccions arquitectòniques, figures geomètriques en la decoració…).
• Cal posar en relleu la presència i les contribucions de les dones en la història de la matemàtica, del seu esforç afegit per vèncer les restriccions que els costums de la seva època imposaven a la seva educació científica. Figures com Hipàcia d’Alexandria, Caroline Herschel, Émilie du Châtelet, Mary Somerville, Sophie Germain, Maria Gaetana Agnesi, Ada Lovelace, Florence Nightingale, Mary Everest Boole, Sófia Kovalévskaia, Emmy Noether, Dorothy Vaughan, Katherine Johnson i Maryam Mirzakhani, entre d’altres, no només han realitzat contribucions importants en matemàtiques, sinó que també serveixen com a models inspiradors per a les noves generacions. Són referents clau per incentivar la presència femenina en els estudis matemàtics i en els àmbits STEM en general.
• Ressaltar les aportacions matemàtiques de cultures diverses i la importància dels intercanvis culturals. Les matemàtiques han prosperat, a vegades de manera decisiva, en moments i llocs diversos com Mesopotàmia, Egipte, les cultures precolombines d’Amèrica, el món islàmic, l’Índia i la Xina. Reconèixer i apreciar les aportacions d’aquestes cultures ajuda a valorar la matemàtica com a coneixement compartit per tota la humanitat. És molt recomanable, en aquest sentit, el llibre La cresta del pavo real: las matemáticas y sus raíces no europeas, de George Gheverghese (Gheverghese, 1996). El desenvolupament de les matemàtiques ha estat sovint el resultat d’intercanvis culturals, i destacar-ho fomenta una apreciació més profunda del paper global de les matemàtiques. Aquest aspecte també enllaça amb el saber #SOE.CE.P. Un gran llibre.
• Cal esmentar també persones de Catalunya que han fet contribucions rellevants en matemàtiques i en educació matemàtica: Lluís Antoni Santaló, Pere Pi Calleja, Pere Puig Adam, Maria Antònia Canals… La FEEMCAT, en el marc dels Congressos Catalans d’Educació Matemàtica, elabora una Línia del Temps per posar en relleu dones i homes que s’han distingit per les seves aportacions a l’aprenentatge de les matemàtiques dels nois i noies catalans.

P. Percepció de la matemàtica com una part crucial del patrimoni cultural de la humanitat, tant per la seva funció instrumental com per l’harmonia, la bellesa i la potència del seu cos de coneixement.

Aquest saber fa referència a la necessitat que l’alumnat entengui la matemàtica no com un conjunt de regles, habilitats de càlcul i procediments, sinó com un cos sòlid de coneixements ple de connexions i aplicacions, com una matèria que convida a la comprensió profunda, al raonament, a compartir idees, a col·laborar, com un territori de coneixements bell, útil, construït al llarg de segles per l’esforç humà i accessible per a tothom.

Bertrand Russell, en l’assaig The Study of Mathematics (Russell, 1919), afirma:

Les matemàtiques, ben enteses, posseeixen no només veritat, sinó també una bellesa suprema.

Bertrand Russell

i Godfrey H. Hardy, en A Mathematician’s Apology (Hardy, 1940), escriu:

Els models d’un matemàtic, igual que els d’un pintor o un poeta, han de ser bells; les idees, com els colors o les paraules, han de combinar-se de manera harmònica. La bellesa és el primer senyal, ja que en el món no hi ha un lloc permanent per a les matemàtiques lletges.

Godfrey H. Hardy

L’alumnat hauria de percebre que la matemàtica és part de la cultura humana, un patrimoni compartit ple d’harmonia, bellesa i potència per modelar, comprendre i predir el món que ens envolta. Un coneixement universal però, alhora, proper i accessible a tothom, en particular, a cada alumne.