Sabers
- Observació i determinació de la regla de formació d'un patró numèric o geomètric.
- Observació de regularitats en diferents contextos matemàtics que permetin extreure conclusions o descobrir propietats.
Estudiar patrons dona l’oportunitat a l’alumnat d’observar, conjecturar, experimentar, descobrir i generalitzar en múltiples situacions: numèriques, de mesura, geomètriques, estocàstiques i algebraiques, és a dir, en tots els sentits de la matemàtica de secundària. Però també són una bona font de contextos per estudiar relacionats amb l’entorn proper a l’alumnat. Permeten connectar les matemàtiques amb la música, les arts visuals, l’escriptura, les ciències i la tecnologia.
Identificar patrons ajuda l’alumnat a desenvolupar la capacitat de raonament lògic i els permet descobrir i comprendre seqüències i regularitats en àmbits diversos, fet essencial en la resolució de problemes. D’altra banda, treballar amb seqüències numèriques, geomètriques o algebraiques afavoreix arribar a la comprensió conceptual de molts objectes matemàtics. Per exemple, estudiant patrons desenvolupem el pensament algebraic, que serà clau per arribar posteriorment a la idea de funció.
Cal remarcar la diferència entre una seqüència o successió, que és un conjunt ordenat d’elements, i un patró, que és la regularitat, si existeix, que marca l’estructura d’una successió.
A 1r d’ESO, l’alumnat seguirà i aprofundirà en el treball de patrons fet al llarg de primària: investigar patrons numèrics i geomètrics i expressar-los matemàticament, ja sigui verbalment o a través de símbols.
Un model adequat per treballar seqüències és, en primer lloc, buscar el següent terme; a continuació, buscar un terme proper; després, un terme llunyà, i, finalment, si es considera oportú, el terme general. Per tal de determinar aquest terme general es fa molt necessari un treball ordenat. L’ús de taules per recollir les dades serà, en molts casos, determinant a l’hora de buscar el patró que segueix la seqüència i, per fer-ho, caldrà fixar-se no només en el resultat de cada terme, sinó també en el procés que s’ha seguit per obtenir-lo. A 1r d’ESO es pot buscar el terme general sense la necessitat d’expressar-lo de forma algebraica.
No s’han indicat de manera específica connexions amb sabers d’altres sentits perquè hi són de forma molt àmplia; és a dir, podem incloure els patrons per treballar bona part dels sabers de 1r d’ESO. Així, dins de numeració podem treballar patrons quan estudiem relacions de paritat, múltiples i divisors, potències o nombres decimals. En l’estudi de la geometria i si fem mesura també podem incloure-hi patrons, per exemple, per deduir els angles dels polígons regulars, per veure com varia el perímetre o l’àrea de diferents figures en fer-les créixer o en estudiar els eixos de simetria d’algunes figures.
En el cas del sentit estocàstic, podem plantejar situacions de canvi quan estudiem estadística. Per exemple, sabent les mesures de centralització d’un conjunt de dades, què passarà si sumem una constant a cadascuna de les dades? I si les multipliquem per una constant, quins canvis hi haurà?
Com ja s’ha esmentat anteriorment, és important incloure l’estudi de patrons numèrics, geomètrics o visuals quan estem treballant la resta de sentits del currículum. La cerca de regularitats, l’establiment de conjectures, la descoberta i la generalització no només són pròpies del sentit algebraic, on hi ha el bloc de patrons, sinó que són accions que traspassen tots els sentits.
També cal remarcar que, en funció de l’organització i planificació de cada centre, a 1r d’ESO pot ser el moment d’introduir el llenguatge algebraic i fer el pas a trobar generalitzacions formals en casos molt senzills. Si es considera que encara no és el moment d’introduir el llenguatge algebraic, el professorat ha de tenir cura que l’alumnat expressi els patrons verbalment amb llenguatge precís.
L’ús de material pot ajudar a entendre el problema, així com a resoldre’l i descobrir-ne la pauta. A la campanya Laboratori de matemàtiques del CREAMAT podem trobar propostes per treballar patrons amb diferents materials: pattern blocks i cubets encaixables, entre d’altres.
Un dels repositoris per trobar bones investigacions que tractin sobre patrons (saber #1.ALG.PA.A i saber #1.ALG.PA.B) és el recull Fem Matemàtiques, una campanya del CREAMAT que recull gairebé tots els problemes de la primera fase, les finals territorials i les fases finals del concurs. Podem trobar els problemes classificats per blocs temàtics, grups d’edat o anys. Un exemple del que s’hi pot trobar n’és el següent problema, de l’any 2014: Xiprers i pomeres.
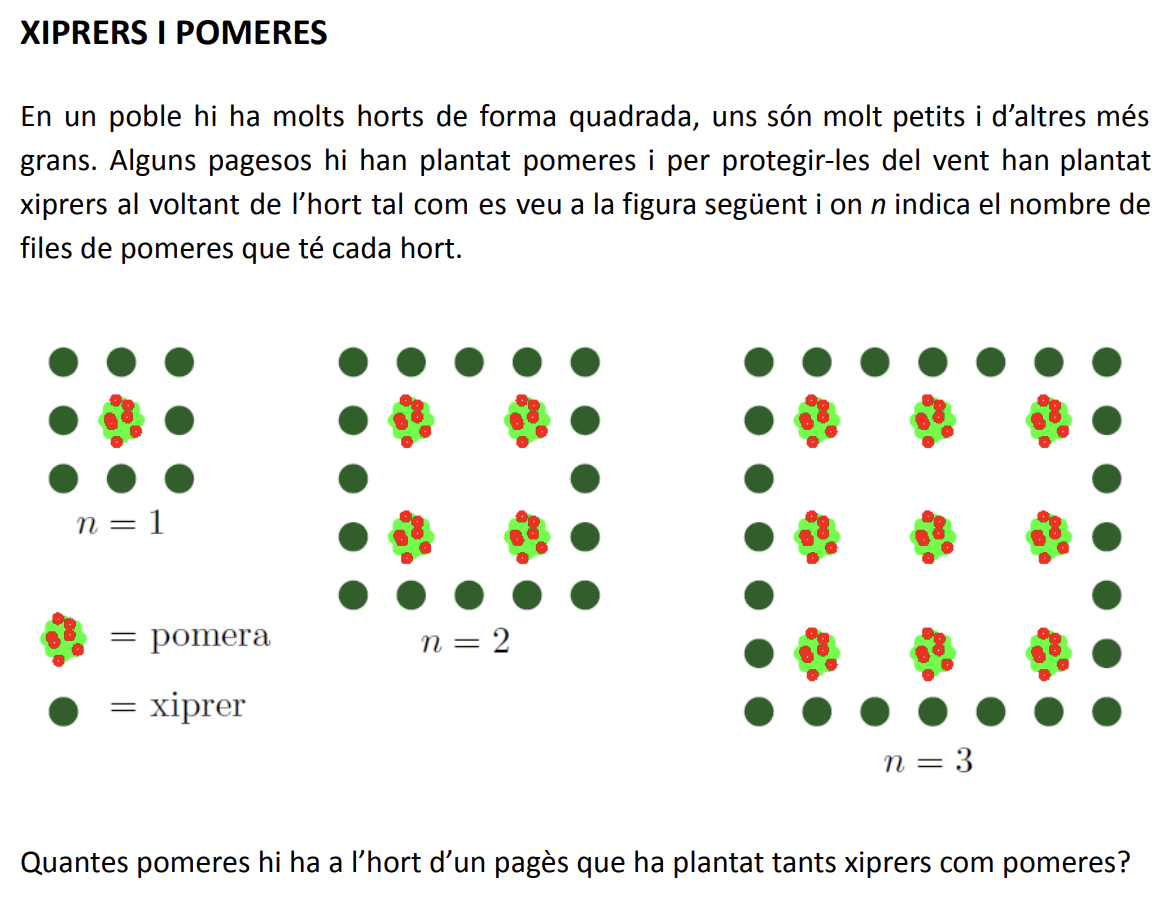
Més enllà que el problema tracti de patrons, cal esmentar les característiques de la majoria de propostes de la primera fase del Fem Matemàtiques: són problemes oberts, requereixen temps per investigar i posen en marxa tots els processos matemàtics, així com la gestió socioemocional.
Al bloc Banc de recursos del Fem Matemàtiques, creat per la Mireia López i la Cyntia Riquelme, podem trobar el problema comentat, i l’anàlisi de diferents resolucions fetes per l’alumnat. Es pot veure com troben eines per arribar al resultat organitzant les dades en taules per observar patrons. Hi ha alumnat que obté l’expressió verbal del patró, hi ha qui arriba a obtenir una expressió semialgebraica, i uns quants obtenen fórmules. En paraules de les autores del bloc:
Pensem que això és suficient per, mitjançant bones preguntes, portar-los a construir aquest llenguatge matemàtic en un context d’aula. Sobretot cal mostrar-los la seva potència i la seva riquesa i, així, fer de la introducció a l’àlgebra una eina necessària per a ells.
Es pot trobar una anàlisi i reflexió sobre aquest problema, i d’altres d’interessants, a l’article Problemas ricos en argumentación para secundaria: reflexiones sobre el pensamiento del alumnado y la gestión del profesor (Morera et al., 2012).
A continuació, es presenten altres idees sobre recursos i activitats d’aprenentatge que poden contribuir a l’adquisició dels sabers d’aquest bloc.
Tot seguit, veurem un exemple de com podem estudiar patrons quan estem treballant múltiples i divisors. Es tracta de l’activitat Obrint i tancant portes del Joan Jareño, que podem trobar a l’ARC. Es proposa un joc d’obrir i tancar portes d’un hotel seguint unes regles marcades pel professorat relacionades amb els múltiples de 2, de 3, de 4... La situació es pot representar repartint a cada alumne un full numerat. El problema convida a conjecturar quines seran les portes que quedaran obertes al final (cercar la pauta) i, en una segona part, a justificar-la.
L’enunciat pot ser el següent: Imaginem un hotel amb un recepcionista juganer. Una nit organitza el següent joc: demana pels altaveus a totes les habitacions que obrin les portes (posem que hi ha 100 habitacions). Després ordena: «Que les portes parells es tanquin!». Així, les portes 2, 4, 6... queden tancades i les 1, 3, 5... queden obertes. Més tard torna a donar una altra ordre: «Que les habitacions múltiples de 3 canviïn la seva situació!». Canviar la situació significa que, si la porta està oberta, s’ha de tancar i, si està tancada, s’ha d’obrir. Així, la porta 3, que estava oberta, s’haurà de tancar, però la 6, que estava tancada, s’haurà d’obrir. A continuació, el grum va seguint: «Els múltiples de 4, que canviïn la seva situació!». «I ara els múltiples de 5!». I continua. Al final del joc, quines portes quedaran obertes?
Després d’experimentar durant una estona amb la situació que deixa el recepcionista després de cada ordre, podem demanar a l’alumnat que «conjecturi» quines portes quedaran obertes. Les portes que quedaran obertes són la 1, 4, 9, 16, 25... És la seqüència dels quadrats perfectes. També la podem descobrir observant que d’un nombre a l’altre s’hi passa sumant senars consecutius: 1+3=4; 4+5=9; 9+7=16…

Un cop descobert el patró, en una segona part i segons el nivell, es pot continuar investigant què el justifica. La raó és que els quadrats perfectes són els únics que tenen una quantitat senar de divisors. A cada porta amb un número que no és quadrat perfecte se li aplica una quantitat parell d’accions: obrir-tancar. A les portes amb quadrats perfectes se’ls fan accions senars: obrir-tancar-obrir. Per poder observar el patró, veiem que tots els números tenen un nombre parell de divisors, menys els quadrats perfectes.
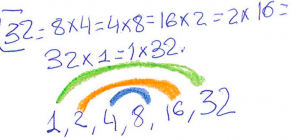
Una proposta per portar a terme al llarg d’una sola sessió és la següent, en què també podem veure com els patrons geomètrics permeten que l’alumnat raoni tant des del punt de vista espacial com numèric:
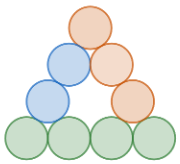
Per quants cercles està format el següent triangle equilàter? Com ho has comptat?
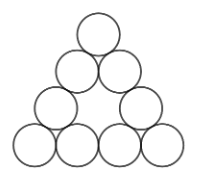
És important demanar, en aquesta primera instància, com ho han comptat, perquè aquestes diferències de comptatge estan relacionades amb les diferències que s’expliquen en el pas n.
Si ara tinguéssim un triangle equilàter el costat del qual està format per 10 cercles en lloc de 4, quin seria el nombre total de cercles que formaria el triangle? I si al costat hi hagués exactament 50 cercles? O 100?
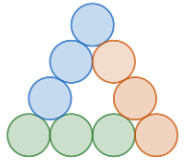
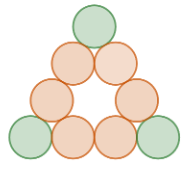
Part de la riquesa d’aquest tipus d’activitats és que permeten encarar-les de diverses formes i val la pena que a classe dediquem temps a explorar totes les que hagin sortit. Es pot aprofitar per classificar les diferents resolucions en funció de com s’ha fet el recompte i discutir si dues estratègies representen la mateixa forma de comptar o són, en realitat, diferents. Algunes opcions de les moltes que hi ha per fer el recompte són les següents:
 |
 |
 |
| Triangle de base 4 cercles:
3 + 3 + 3 = 3 · 3 = 9 Triangle de base 50 cercles: 49 + 49 + 49 = 3 · 49 = 147 Triangle de base 100 cercles: 99 + 99 + 99 = 3 · 99 = 297 Triangle de base n cercles: (n-1)+ (n-1) + (n-1) = 3 · (n-1) |
Triangle de base 4 cercles:
4 + 3 + 2 = 9 Triangle de base 50 cercles: 50 + 49 + 48 = 147 Triangle de base 100 cercles: 100 + 99 + 98 = 297 Triangle de base n cercles: n+ (n-1) + (n-2) = 3n - 3 |
Triangle de base 4 cercles:
3 + 3 · 2 = 9 Triangle de base 50 cercles: 3 + 3 · 48 = 147 Triangle de base 100 cercles: 3 + 3 · 98 = 297 Triangle de base n cercles: 3 + 3 · (n-2) = 3n - 3 |
En funció de si ja s’ha introduït el llenguatge algèbric o no, es podrà arribar a la generalització amb la fórmula o deixar-ho per a cursos posteriors, però, sigui com sigui, l’alumnat ha de ser capaç d’expressar verbalment com fa el recompte. Hem de demanar-li que expressi la regla de formació del patró de la manera més senzilla possible, fent servir de forma correcta el vocabulari. L’ús de material manipulable pot ajudar a visualitzar i entendre la situació que cal resoldre.
Podríem ampliar el problema plantejant-lo sobre un quadrat en lloc d’un triangle equilàter, i preguntar-nos quins canvis ens hi podem trobar abans de començar a investigar.
Un bon moment per buscar regularitats (saber #1.ALG.PA.B) és el de la pràctica productiva, per exemple, quan es treballen les operacions combinades dins el bloc Sentit de les operacions del sentit numèric. Es podria posar un patró com el següent i demanar als alumnes què hi observen:
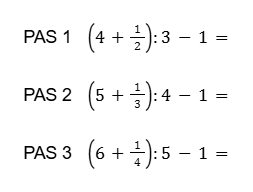
Aquesta activitat l’hem anomenat Pràctica productiva d’operacions combinades per poder fer l’anàlisi competencial.
Llicenciat sota la Llicència Creative Commons Reconeixement CompartirIgual 4.0