Sabers
- Ús de factors de conversió que permetin comparar unitats de mesura d’angles i l’establiment del radian com a unitat internacional de mesura.
[ESS]
Orientacions curriculars de matemàtiques de l’ESO
Magnitud
Descripció i orientacions
Reflexions generals
Els angles i la seva obertura ja han estat objecte d’estudi a la primària i en tots els cursos fets de la secundària. Les unitats utilitzades fins aleshores per mesurar-los han estat principalment les del sistema sexagesimal, un sistema de numeració posicional amb base 60 emprat pels sumeris entre el 3000 aC i el 2000 aC, i que actualment utilitzem per a la mesura del temps horari i l’amplitud dels angles. En el bloc de magnitud hem cregut necessari afegir un saber que permeti a l’alumnat treballar amb les unitats adequades de mesura d’angles, establir comparacions entre elles i fins i tot fer operacions si les situacions així ho requereixen. Proposem que en aquest curs l’alumnat descobreixi altres sistemes de mesura angular com el centesimal o francès, i l’internacional; i ho faci aprofitant el context històric i social on apareixen. L’establiment d’una unitat de mesura per als angles que depèn exclusivament d’una propietat mètrica de la circumferència, i la conversió d’altres unitats habituals, com les del sistema sexagesimal, a aquesta, serà fonamental per al desenvolupament de situacions de mesurament on intervenen relacions entres longituds i angles.
Comentaris sobre els sabers essencials i d’ampliació
El fet de concretar un únic saber en aquest bloc ens ha portat directament a proposar-lo com a essencial. Igualment, pensem que és molt important la concepció del radian com a unitat de mesura d’angles, en tant que esdevé unitat en el sistema internacional i, a més a més, permet recollir sabers anteriors relacionats amb la longitud de la circumferència i el treball amb els seus elements, com són l’arc, angle central, etc., propis del sentit espacial. Volem destacar també que l’ús de factors de conversió per comparar unitats en el sistema sexagesimal, per exemple, amb els radians, permetrà treballar el raonament proporcional i alhora és una bona oportunitat per recollir sabers de cursos anteriors on són presents el càlcul amb angles i les seves expressions dins del sistema sexagesimal, tant en forma complexa com incomplexa.
Recursos i activitats
Recursos i activitats per treballar sabers concrets
A continuació, es presenten algunes idees sobre recursos i activitats d’aprenentatge que poden contribuir a l’adquisició dels sabers d’aquest bloc.
A. Identificació d’atributs mesurables en objectes matemàtics o físics, en el nostre entorn.
Per treballar el saber #4.MES.MA.A proposem activitats que a partir del raonament i la representació ajudin a fer que l’alumnat entengui la unitat de mesura del radian fins al punt que el puguin utilitzar per fer mesuraments i estimacions de magnituds angulars. A més a més, per tal que la comprensió sigui plena és convenient que pugui comparar-se amb unitats ja conegudes per l’alumnat, com són les del sistema sexagesimal.
Comparació de mesures angulars
Qualsevol experimentació de mesurament d’angles o de trigonometria és una bona oportunitat per treballar les unitats. Els angles es poden donar tant a l’inici de l’activitat com en el seu desenvolupament, així com en els resultats. Els podem trobar en forma complexa (graus, minuts i segons) o incomplexa, si s’ha treballat en el sistema sexagesimal o en el centesimal. Així doncs, a partir de l’estudi de la precisió en les mesures o de la conveniència a l’hora de triar una unitat o una altra, sorgeix la possibilitat de passar d’aplicar els factors de conversió. És important que l’alumnat entengui i sàpiga resoldre aquestes conversions i operacions bàsiques amb angles, ja sigui de manera escrita o directament amb l’ús de la calculadora.
En situacions de girs, trobem dos sentits d’obertura dels angles, així com alguns que superen la volta sencera. Naturalment, en un mesurament hi ha una quantitat associada a una unitat. En aquest sentit, la conversió entre unitats també es pot treballar a partir de la imatge d’obertura que proporciona l’angle.
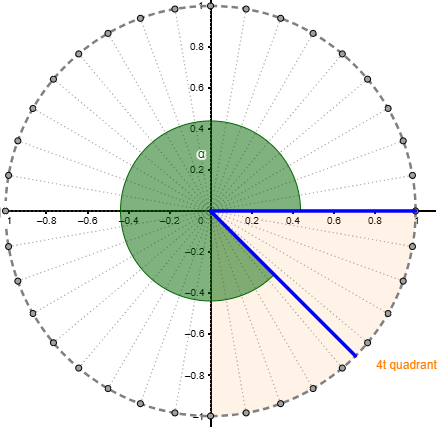
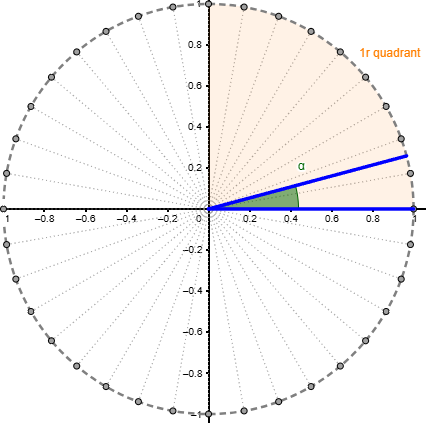
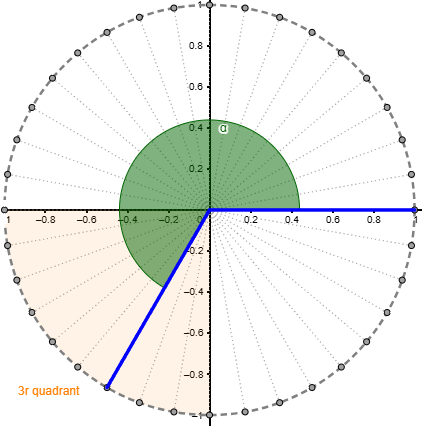
Per a això, pot ser útil el full de treball Equivalència entre graus i radians, del professor Manel Martínez, que inclou una aplicació en la qual, a més de permetre introduir l’expressió d’un angle en una unitat o en una altra, es mostra la seva representació sobre la circumferència goniomètrica, s’especifica en quin quadrant es troba i es realitza la conversió.
És previsible que, a aquestes edats, l’alumnat tingui clar quants graus representen un angle recte, un pla o un complet. A més, les aplicacions de GeoGebra, a banda de ser molt útils per a l’aprenentatge, són essencials per a la comprovació de resultats.
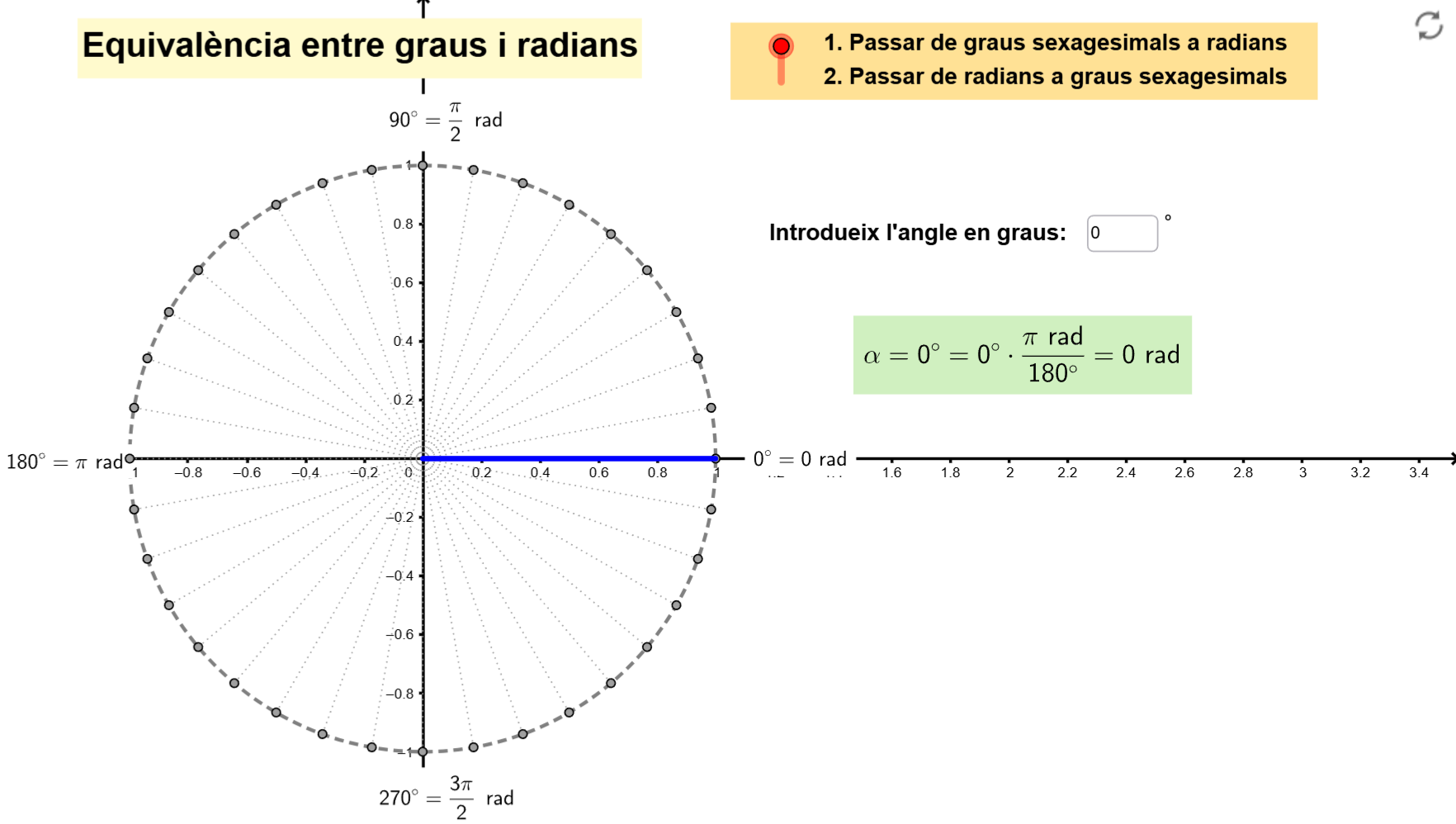
El treball de conversions entre graus i radians ajudarà a identificar la mesura d’algunes fraccions d’angle en radians. Per aquesta raó no hem de perdre l’oportunitat de fer alguna proposta del tipus: Quants radians mesuren els angles següents?
 |
 |
 |
 |
 |
 |
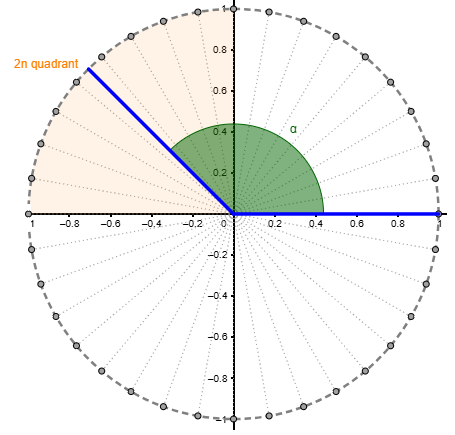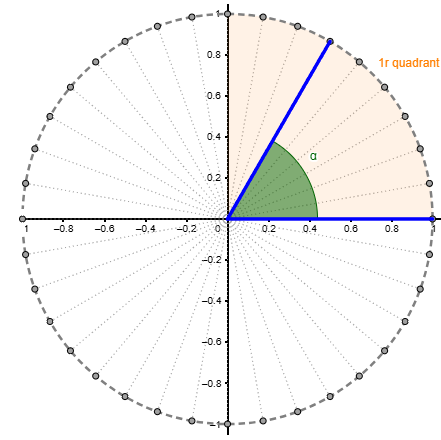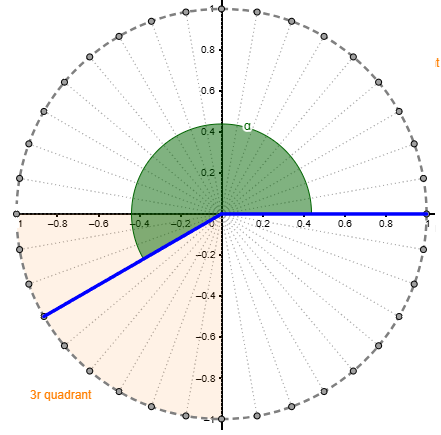Font: Equivalència entre graus sexagesimals i radians
Autor: Manel Martínez
És important fomentar que sorgeixin diferents estratègies per resoldre-ho. Hi ha alumnes que decideixen passar per la mesura de l’angle en graus i després fan el canvi d’unitats a radians. Altres parteixen de l’equivalència entre un angle pla i 𝜋 rad, i operen a partir de fraccions d’aquest angle. Aquestes situacions esdevenen bones oportunitats per compartir els raonaments que van sortint i incrementen els seus aprenentatges amb l’adquisició d’altres maneres de pensar.
Aprofitant l’ocasió, es pot proposar l’activitat inversa: donar l’amplitud de l’angle en radians i demanar a l’alumnat que el representi. Es recomana sempre donar mesures múltiples d’un dotzena part de 𝜋 rad, és a dir, múltiples de 15°.
Llicenciat sota la Llicència Creative Commons Reconeixement CompartirIgual 4.0