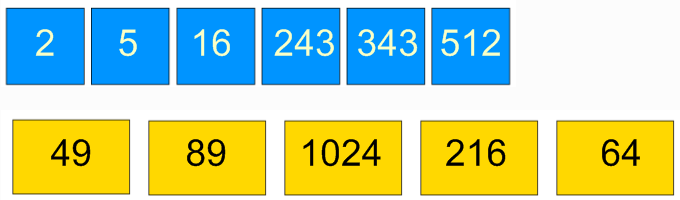
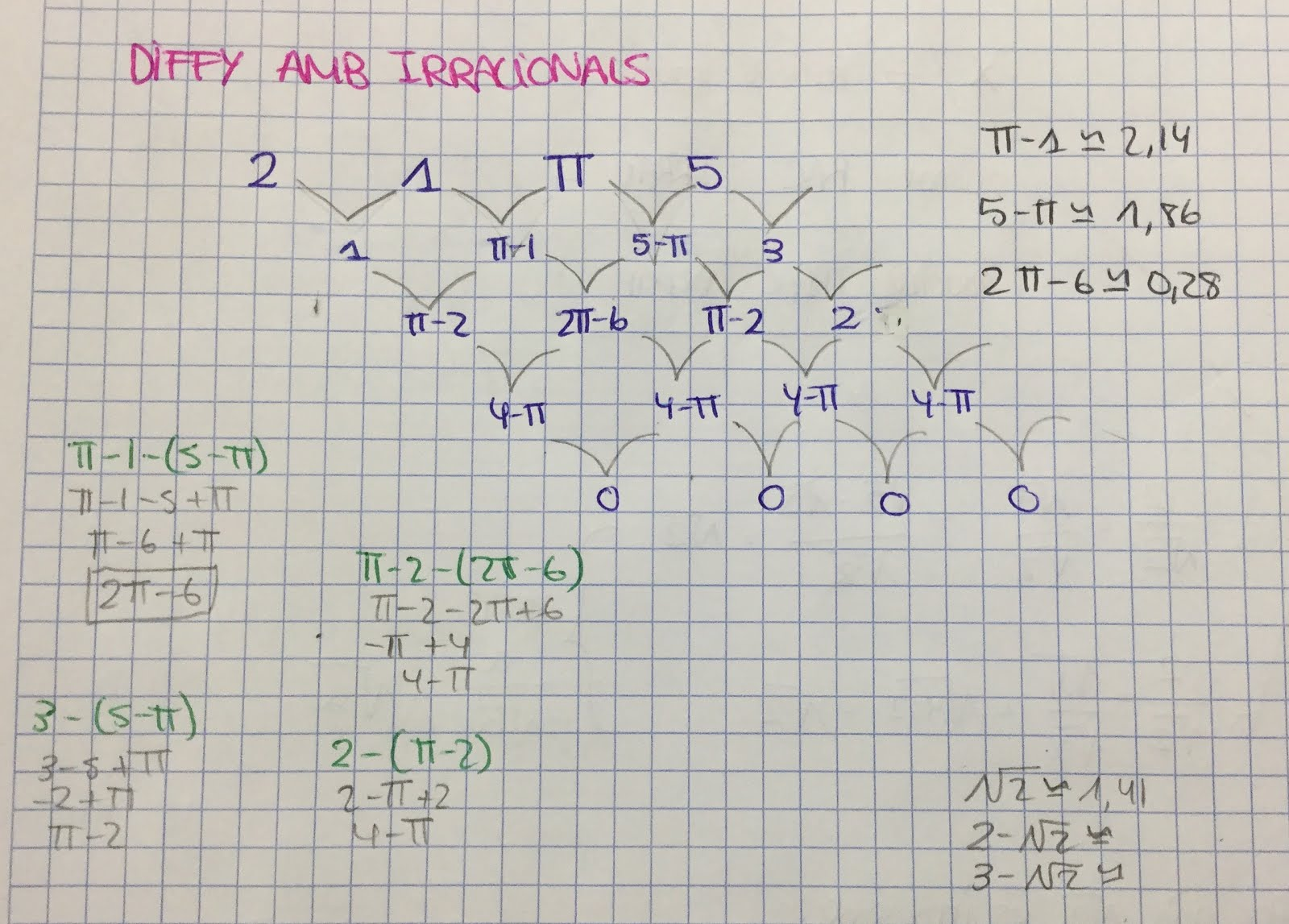
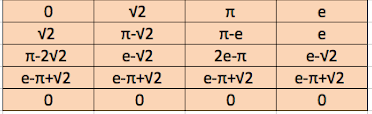
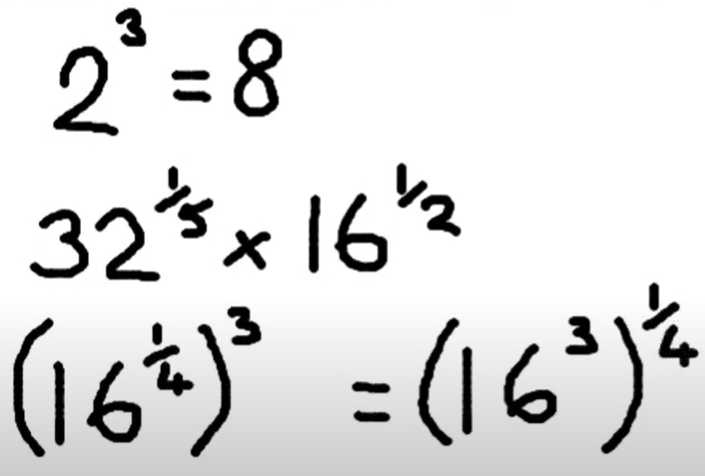L’ús de recursos digitals, com ara calculadores i fulls de càlcul, per a la construcció de coneixement sobre les propietats aritmètiques d’arrels i altres nombres irracionals, saber #4.NUM.SO.B, és fonamental en l’aprenentatge actual de les matemàtiques. Aquests recursos permeten explorar i comprovar propietats de manera ràpida i precisa, i faciliten la comprensió de conceptes complexos mitjançant simulacions i visualitzacions. A més, fomenten l’autonomia i la investigació, ja que ofereixen l’oportunitat d’experimentar amb dades reals i abstractes, i afavoreixen una anàlisi més profunda dels resultats.
A continuació, es descriu l’activitat The root of the problem, del web del NRICH, que permet treballar el saber #4.NUM.SO.A i, alhora, utilitzar recursos digitals, saber #4.NUM.SO.B. Aquesta activitat destaca la importància d’utilitzar aquests recursos de manera adequada i fomenta la reflexió sobre l’eficiència de les eines digitals, així com la valoració de quina eina és més útil en cada situació.
Planteja el repte de calcular la suma:
\(\displaystyle\frac{1}{\sqrt{1}+\sqrt{2}}+\frac{1}{\sqrt{2}+\sqrt{3}}+\dots+\frac{1}{\sqrt{99}+\sqrt{100}}\)
Aquesta activitat ofereix una oportunitat per practicar la racionalització d’arrels i posa de manifest la importància de no arrodonir els resultats abans d’hora. Si es mantenen els radicals en el càlcul i se simplifica tant com sigui possible, s’arriba a una conclusió interessant: el resultat final és un nombre enter. Aquest resultat pot passar desapercebut si els estudiants fan el càlcul amb calculadora.
Per resoldre el repte, es pot utilitzar un full de càlcul, en què l’alumnat pot començar trobant una expressió per a \(\frac{1}{\sqrt{1}+\sqrt{2}}+\frac{1}{\sqrt{2}+\sqrt{3}}\) i anar afegint termes progressivament.