Successions de creixement

Per introduir el saber #4.ALG.PA.A, una possibilitat és començar amb la comparació de diferents ritmes de creixement de successions.

Podem partir de successions senzilles com ara la dels nombres parells i la dels senars i preguntar com creixen. Fàcilment, es veurà que creixen «a la mateixa velocitat». Després podem proposar altres successions de creixement lineal, de creixement quadràtic o exponencial i demanar si totes creixen de la mateixa manera. La pregunta és volgudament oberta per fomentar i conduir la conversa a l’aula i, davant de les hipòtesis que vagin fent els alumnes, se’n pot demanar una justificació. En aquest cas, serà important veure les diferents estratègies i formes de representar la situació per part de l’alumnat i fer-ne una posada en comú.

Posteriorment, es poden introduir successions convergents i trencar la idea que totes les successions que creixen tenen suma infinita. Una bona activitat pot ser l’estudi de la successió \(\dfrac{1}{2^n}\), que es pot plantejar en un context numèric quan es treballen les fraccions en contextos històrics, tal com s’ha plantejat a #2.NUM.QU.B en l’activitat Les fraccions: l’ull d’Horus. En aquest cas, es parteix del mite egipci que diu que les parts que formaven l’ull d’Horus representaven les fraccions \(\dfrac12\), \(\dfrac14\), \(\dfrac18\,\ldots\), \(\dfrac{1}{64}\) i que tot ell representava la unitat. A 4t d’ESO, proposem un enfocament del mateix problema, però des del punt de vista de les successions. Es tracta d’una progressió geomètrica decreixent de suma infinita igual a 1. Aquest últim és un concepte nou i poc intuïtiu per al nostre alumnat, per la qual cosa és important dotar-lo de sentit per poder acabar passant a l’abstracció i al càlcul de límits en estudis posteriors.

En l’article «Diàleg entre iguals a l’aula. Eina per a la construcció del coneixement matemàtic» del Xavier Vilella, s’hi pot trobar una possible forma de gestió de l’activitat per afavorir el descobriment, a més d’altres activitats de cerca de patrons i consideracions interessants sobre com gestionar el diàleg matemàtic a l’aula.

En aquest sentit, la visualització geomètrica del problema és una gran ajuda per mostrar la convergència:

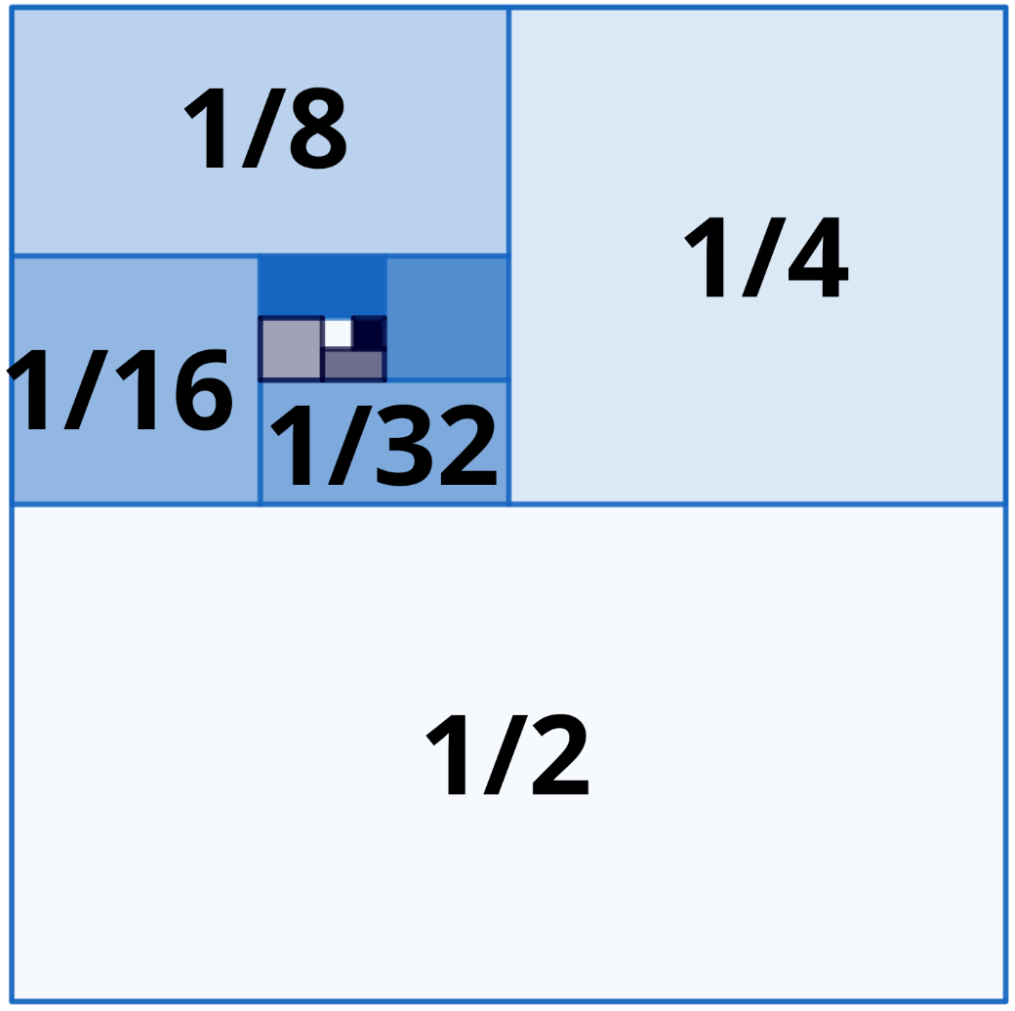
Es pot demanar’ que cerquin altres successions convergents, amb representacions que ho mostrin, com per exemple aquesta altra:

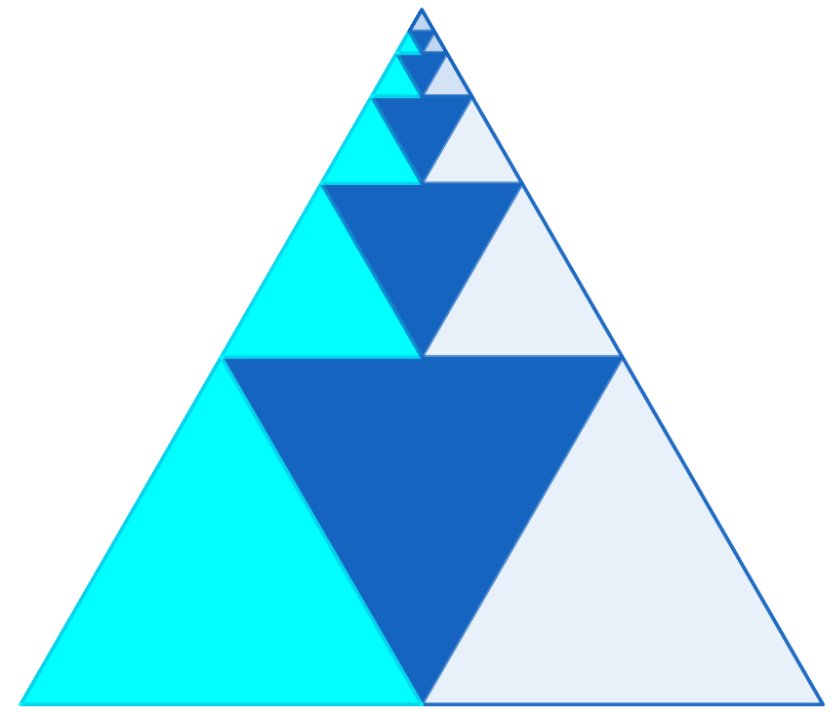
En la mateixa línia que els darrers exemples, hi ha l’activitat proposada pel MMACA Una suma d’infinits termes. L’activitat proposa observar el quadrat següent:

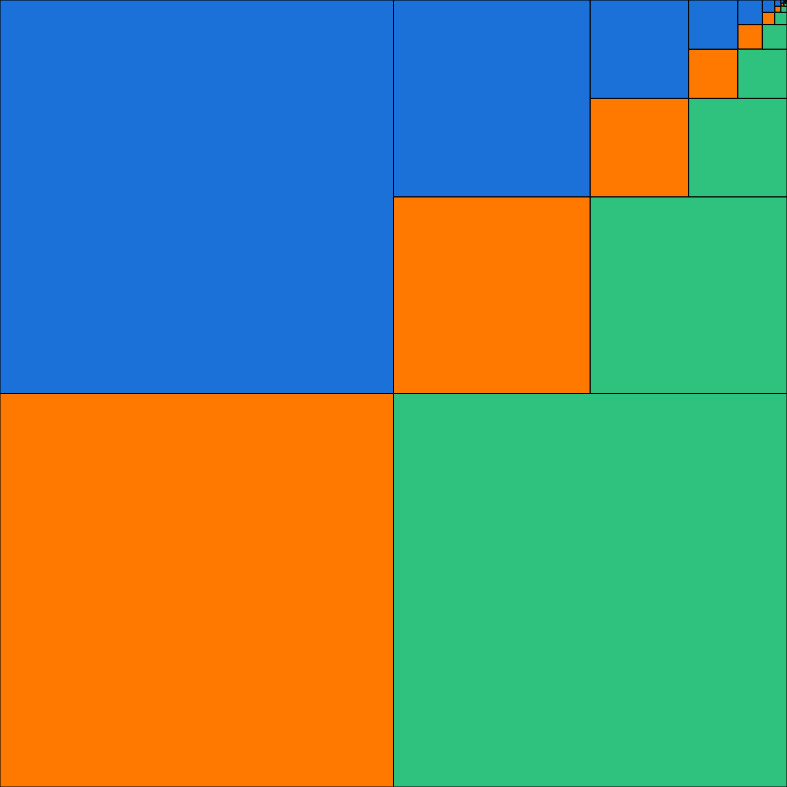
Aquest quadrat està format per tres sèries de quadrats marcats amb tres colors diferents. Cada sèrie comença per un quadrat de superfície 1/4 del quadrat general. El segon terme és 1/4 de l’anterior, per tant, és 1/16 del total. I se segueix d’aquesta mateixa manera amb quadrats cada cop quatre vegades més petits. Es tracta d’una suma d’infinits termes. Com que les tres sumes són iguals, cadascuna és 1/3 del quadrat general.

\( \dfrac14 +\dfrac1{16}+\dfrac1{256}+\cdots \)

La proposta va acompanyada d’un full descarregable per poder fer l’activitat doblegant-lo i un petit vídeo que il·lustra com fer els plecs.

En relació amb el saber #4.ALG.PA.A, proposem l’activitat El triangle aritmètic que busca la descoberta del triangle de Pascal i la cerca de patrons a l’interior. És una activitat que es podria plantejar perfectament en cursos anteriors, però es proposa a 4t d’ESO per les fortes connexions que té tant amb el sentit numèric pel que fa a les tècniques de recompte, com amb el mateix sentit algebraic per l’aplicació a l’hora de desenvolupar un binomi, en cas que es consideri que es vol anar una mica més enllà en el treball amb les identitats notables.

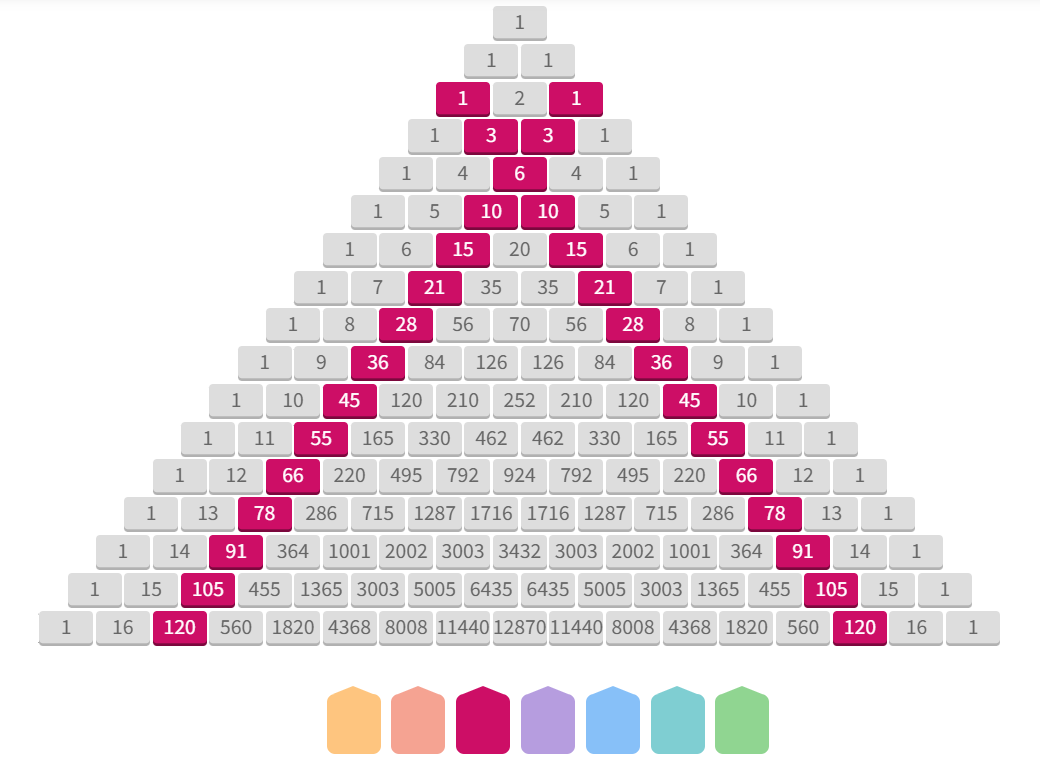
El punt de partida de l’activitat és justament fer un recompte del nombre de camins que porten a cada una de les caselles de la figura següent, entenent que només és possible moure’s cap avall. No s’accepten moviments laterals ni cap amunt. Es pot imaginar que es deixa caure una bola des del vèrtex superior i aquesta pot agafar el camí de la dreta o de l’esquerra quan es troba en una bifurcació:

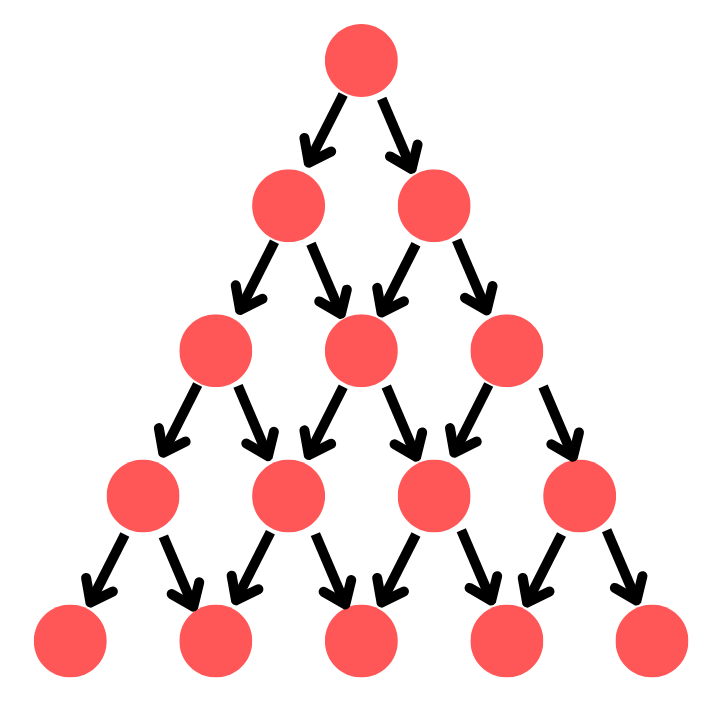
Resulta senzill omplir les primeres caselles, però tal com anem baixant en l’estructura es fa necessari un treball ordenat i sistemàtic per obtenir tots els camins possibles. Després que l’alumnat hagi investigat durant “una estona”, es posen en comú els resultats i es demana que emplenin les dues files següents. En aquest moment, la cerca exhaustiva és prou complicada de fer sense oblidar cap camí, amb la qual cosa forcem a buscar raonaments que permetin obtenir els resultats sense haver-los de buscar. La gestió del docent per conduir la conversa i el raonament és clau per arribar a la conclusió (raonada) que cada casella s’obté sumant els nombres de camins que arriben a les dues immediatament superiors. D’aquesta manera, trobem un primer patró que ens permet completar tantes files del triangle com vulguem.

Un cop descobert el triangle aritmètic, l’estudi dels patrons que amaga és una tasca engrescadora i molt interessant. En aquest article interactiu de Mathigon sobre el triangle, podem visualitzar, fàcilment amb colors, alguns dels diferents patrons (nombres naturals, nombres triangulars, nombres tetragonals, seqüència de Fibonacci, etc.), així com investigar altres propietats interessants del triangle que ens connecten amb altres camps com, per exemple, la divisibilitat o les fractals.

Si es vol optar pel format audiovisual, al vídeo Los secretos del triángulo de Pascal del canal Derivando de YouTube, del matemàtic i divulgador Eduardo Sáenz de Cabezón, es pot trobar més informació interessant sobre el triangle..

Aquesta activitat es podria treballar en cursos anteriors (hi ha un problema d’investigació de la primera fase del Fem Matemàtiques 2022, Aneu on l’atzar us porti, per a 1r o 2n d’ESO), però, si es duu a terme a 4t d’ESO, permet connectar amb altres sabers com ara els nombres combinatoris (saber #NUM.CO.A) i d’aquí a la descomposició de potències de binomis, com a possible ampliació.

Potències de binomis

Una possibilitat, si es vol treballar la cerca de patrons algebraics (saber #4.ALG.PA.A), és l’activitat «Potències de binomis», que pretén descobrir les regularitats dins del desenvolupament de les potències d’un binomi.

Per fer-ho, es pot començar operant per trobar el desenvolupament de \( (x+y)^0\), \( (x+y)^1\),\( (x+y)^2\), \( (x+y)^3\), \( (x+y)^4\), \( \cdots\) i observar-ne els resultats. Com més casos calculin, més fàcilment veuran el patró que segueix.

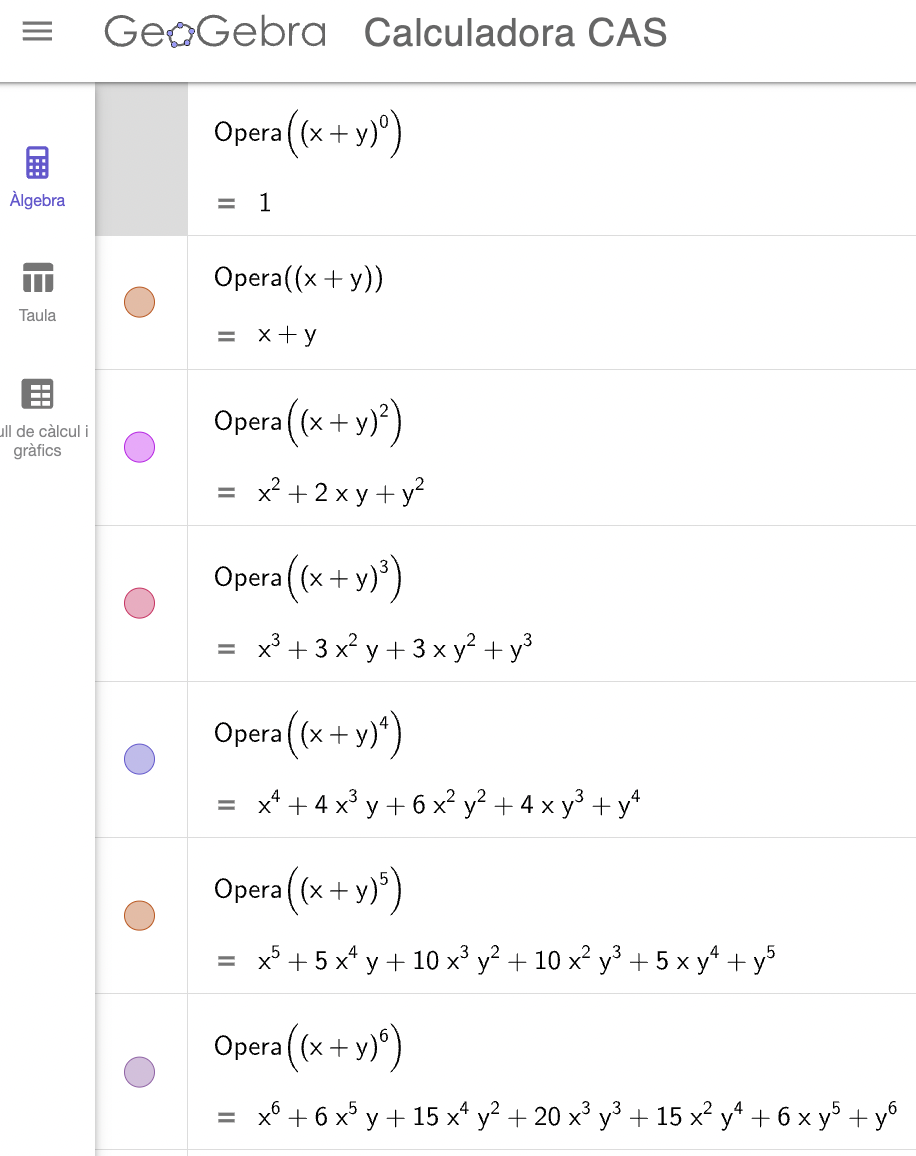
Aquesta activitat resulta molt interessant com a pràctica productiva en la manipulació algebraica. Les diferents velocitats de càlcul de l’alumnat faran que no tots arribin a desenvolupar el mateix nombre de binomis, però la posada en comú dels resultats (disposant-los a la pissarra de manera ordenada, per tal que recordi el triangle aritmètic (treballat prèviament)) els posarà a tots en igualtat d’oportunitats per trobar el patró. Es pot anar guiant la conversa per fer-los veure què passa amb els graus de tots els termes d’un mateix binomi i com va variant en cada terme. Per altra banda, caldrà veure com trobar els coeficients i també, a partir de bones preguntes, guiar-los a la descoberta de la relació amb el triangle aritmètic. El moment de descobriment acostuma a ser de molta sorpresa, ja que, en principi, aquesta activitat no tenia res a veure amb el treball fet anteriorment a partir de la cerca de camins, però porta al mateix triangle.

És un bon moment, doncs, per introduir els nombres combinatoris (saber #NUM.CO.A) aprofitant la necessitat de representar els nombres del triangle si volem escriure l’expressió algebraica del binomi de Newton. Es pot lligar amb el treball d’aquests nombres descrit al sentit numèric.