Patrons

Sabers

Observació i determinació de la regla de formació d'un patró numèric o geomètric. Càlcul del terme general.
[ESS]
Observació de regularitats en diferents contextos matemàtics que permetin extreure conclusions o descobrir propietats.

Descripció i orientacions

Reflexions generals

A 2n d’ESO es proposa la introducció del llenguatge funcional i de les tipologies de funcions més senzilles, tal com es pot consultar al bloc de sabers #ALG.RF. Si tenim aquest fet en l’horitzó, el treball previ de recerca de patrons és fonamental per ajudar l’alumnat a entendre més fàcilment el concepte de funció, ja que es comença treballant amb un domini discret.

Per altra banda, identificar patrons ajuda a desenvolupar la capacitat de raonament lògic i permet a l’alumnat descobrir i comprendre seqüències i regularitats en àmbits diversos, fet essencial en la resolució de problemes.

A 1r d’ESO, i potser a primària, s’haurà treballat la recerca de patrons senzills, tant numèrics com geomètrics. A 2n d’ESO s’espera que l’alumnat assoleixi una certa habilitat i pugui anar més enllà, motiu pel qual les propostes poden ser una mica més complexes. A més, també és possible que s’introdueixi en aquest curs el llenguatge algebraic (si no s’ha introduït ja a 1r), amb la qual cosa es pot acabar buscant una expressió algebraica que permeti generalitzar el patró treballat. Tanmateix, cal remarcar que no cal que sigui sempre l’objectiu final de la recerca de patrons: es podrien tenir dificultats per trobar l’expressió algebraica, o fins i tot ser impossible, però, en canvi, ser capaç d’identificar clarament el patró i explicar-lo de moltes maneres (bé mitjançant representacions o bé amb el llenguatge oral o escrit propi). No hem d’oblidar que el llenguatge algebraic tot just acaba d’entrar en el seu bagatge i és una eina molt potent, però també complexa, i per això alguns alumnes poden tenir dificultats en aquest aspecte i caldrà oferir-los més guiatge i més oportunitats d’aprenentatge. De totes maneres, aquest tipus d’activitats ens proporcionen un bon context per afavorir l’ús d’aquest llenguatge.

Tal com s’esmenta a altres cursos, cal remarcar la diferència entre una seqüència o successió ‒que és un conjunt ordenat d’elements‒ i un patró ‒que és la regularitat, si hi és, que marca l’estructura d’una successió. També cal recordar que un model adequat per treballar seqüències és, en primer lloc, buscar el següent terme, després buscar un terme proper, a continuació un terme llunyà i, finalment, si es considera oportú, el terme general. Per tal de determinar aquest terme general es fa molt necessari un treball ordenat. L’ús de taules per recollir les dades serà, en molts casos, determinant a l’hora de buscar el patró que segueix la seqüència i, per fer-ho, caldrà fixar-se no només en el resultat de cada terme sinó en el procés que s’ha seguit per obtenir-lo.

Comentaris sobre les connexions

No s’han indicat específicament connexions amb sabers d’altres sentits perquè hi són de manera molt àmplia, és a dir, podem incloure els patrons per treballar bona part dels sabers de 2n d’ESO. Així, podem treballar patrons numèrics quan treballem el sentit numèric o patrons geomètrics quan treballem el sentit espacial o el de la mesura, per exemple per veure com varia el perímetre o l’àrea de diferents figures en fer-les créixer. En el cas del sentit estocàstic, podem plantejar situacions de canvi quan estudiem estadística; per exemple, sabent les mesures de centralització d’un conjunt de dades, què passarà si sumem una constant a cadascuna de les dades? I si les multipliquem per una constant, quins canvis hi haurà?

Comentaris sobre els sabers essencials i d’ampliació

Com també es troba reflectit al document de 1r d’ESO, identificar patrons ajuda l’alumnat a desenvolupar la capacitat de raonament lògic. L’estudi de patrons implica observar regularitats, fer conjectures o generalitzar, accions totes elles que permeten treballar el conjunt dels processos matemàtics, des del raonament i prova, la comunicació i representació, les connexions (tant intramatemàtiques com extramatemàtiques) fins a la resolució de problemes, present sempre a tots els blocs dels sabers del currículum. D’aquí el caràcter essencial del saber #2.ALG.PA.A.

A primer es demanava expressar matemàticament els patrons, fos verbalment o per mitjà dels símbols. Ara, a 2n d’ESO, s’inclou la cerca del terme general. El treball dels altres blocs del sentit algebraic donarà les eines perquè l’alumnat pugui començar a expressar les regles de formació dels patrons mitjançant el llenguatge algebraic. Quan treballem el saber #2.ALG.PA.A, el professorat ha de tenir cura que l’alumnat expressi els patrons, si es fa verbalment, amb llenguatge precís i, si es fa amb llenguatge algebraic, aprenent a fer servir els símbols i notació de manera apropiada.

Recursos i activitats

Recursos i activitats generals per al bloc de sabers

L’ús de material pot ajudar a entendre el problema, a resoldre i descobrir el patró. A la campanya Laboratori de matemàtiques del CREAMAT podem trobar propostes per treballar patrons amb diferents materials: pattern blocks i cubets encaixables, entre d’altres.

Una miniaplicació interessant per treballar tot el bloc de sabers és, per exemple, el Mathstick Patterns del web Transum.

També volem fer esment del recull Fem Matemàtiques, un repositori excel·lent per trobar investigacions on la cerca de patrons hi és molt present.

Recursos i activitats per treballar sabers concrets

A continuació, es presenten algunes idees sobre recursos i activitats d’aprenentatge que poden contribuir a l’adquisició dels sabers d’aquest bloc.

A. Observació i determinació de la regla de formació d'un patró numèric o geomètric. Càlcul del terme general. [ESS]

Patrons visuals de creixement

Una proposta per treballar el saber #2.ALG.PA.A, més concretament els patrons visuals de creixement, la trobem al web Visual patterns, on es poden trobar 500 propostes de patrons visuals de diferents nivells de dificultat. A partir dels tres o quatre primers elements del patró i amb el nombre d’objectes enumerats sota cada patró per al pas 43 de la seqüència, l’alumnat ha de trobar la pauta de formació i expressar-la matemàticament. Podem trobar propostes més senzilles en les quals el creixement és constant i d’altres de més complexes (de les quals se’n parlarà al document de 3r curs) on no ho és. Un exemple del primer tipus és el següent:

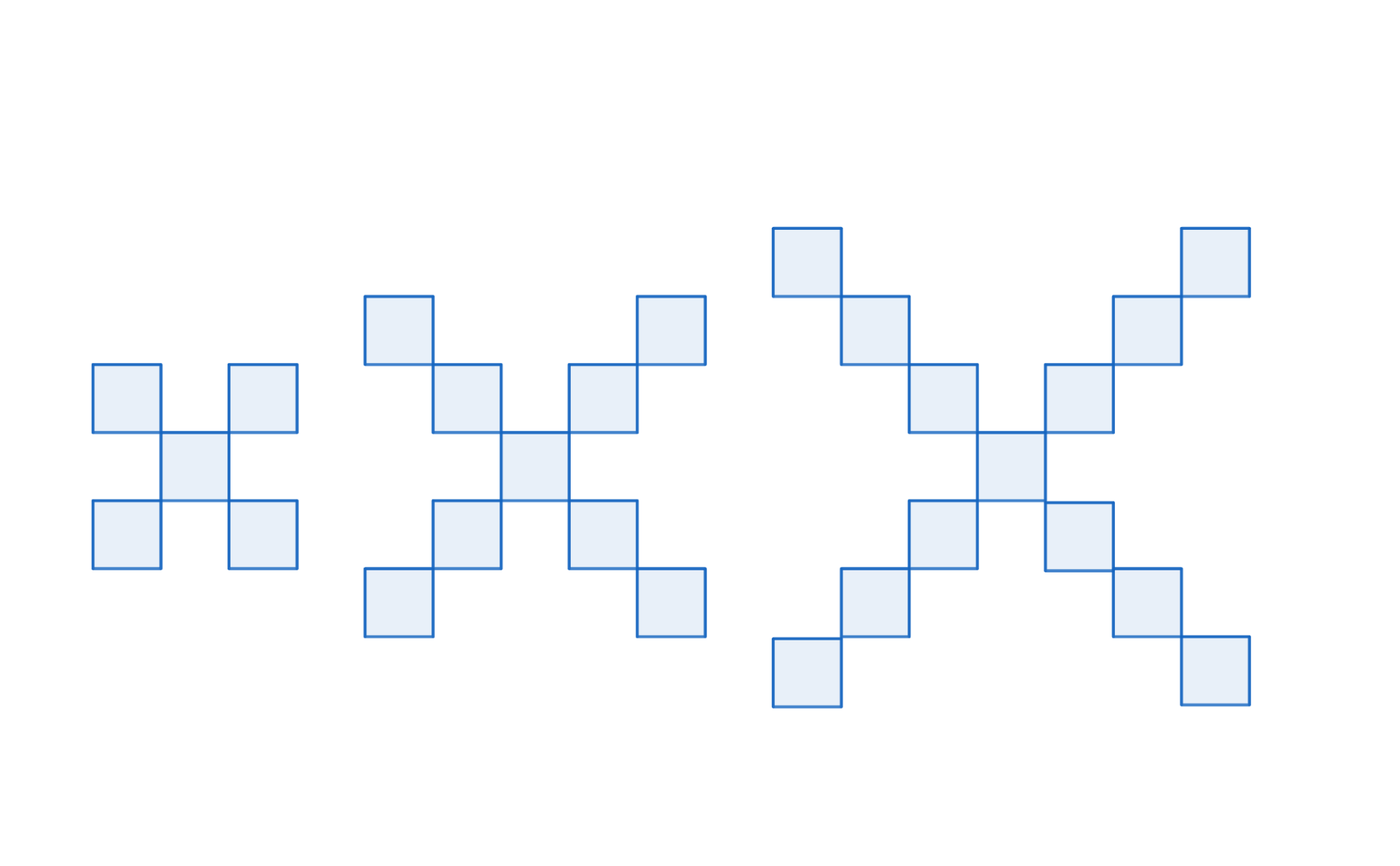
Un cop hàgim presentat el patró a l’alumnat es pot demanar com seguirà la seqüència, és a dir, que dibuixin el següent pas o els dos passos següents. D’aquesta manera ens assegurem que han entès la regla de formació. Tot seguit, convé posar en una taula les observacions, d’aquesta manera serà més fàcil trobar regularitats:

Pas	Nombre de quadrats
1	5
2	9
3	13
…	…

Amb la taula, l’alumnat podrà veure que el nombre de quadrats augmenta de quatre en quatre, és a dir, que a cada pas hi ha 4 quadrats més que a l’anterior. Els demanem que ho posin per escrit i també que expliquin com augmenta; per exemple podrien dir: «posant un quadrat a cadascuna de les 4 puntes de la figura» o «posant 4 quadrats als extrems més allunyats del quadrat central». Poden trobar moltes formes diferents d’expressar-ho.

Ara bé, la taula ens servirà no només mirant-la verticalment (pensament recursiu). La informació més rellevant la podem obtenir observant-la horitzontalment (pensament funcional). Podem plantejar: a partir del número de pas, com trobem el nombre de quadrats? En un primer moment ho poden expressar verbalment: multiplico el pas per 4 i sumo 1. També poden anar fent passos en l’ús de símbols: pas x 4 + 1. I finalment, poden donar l’expressió algebraica: 4n + 1.

És interessant remarcar que a 2n d’ESO fem la proposta d’introduir la funció lineal i afí i, activitats com la que acabem de presentar, estableixen connexions interessants. Podríem acabar fent un gràfic que relacioni el número de pas amb el nombre de quadrats, introduint les relacions funcionals a través del treball de patrons.

Cub pintat

Una altra proposta per treballar el saber #2.ALG.PA.A és Cub pintat del web NRICH. Aquesta proposta tant es pot treballar a 2n d’ESO com a 3r, en funció del treball previ sobre llenguatge algebraic que s’hagi fet a classe.

Es proposa a l’alumnat que imagini un cub gran format per 27 cubets petits de color vermell. Si submergim aquest cub 3x3x3 en un pot de pintura groga i el traiem, haurà quedat pintada de groc tota la superfície exterior. Ara desmuntem aquest cub gran i observem els 27 cubets petits. Podem fer moltes preguntes interessants per cercar pautes: Quants cubets tindran una cara pintada de groc? Quants en tindran dues? Quants no en tindran cap? Quin és el màxim nombre de cares que poden ser grogues? I si en lloc d’un cub 3x3x3, en tenim un 4x4x4, com variarà la resposta a les preguntes anteriors? I si en tenim un 5x5x5? I un 10x10x10? Podeu trobar-hi la pauta general?

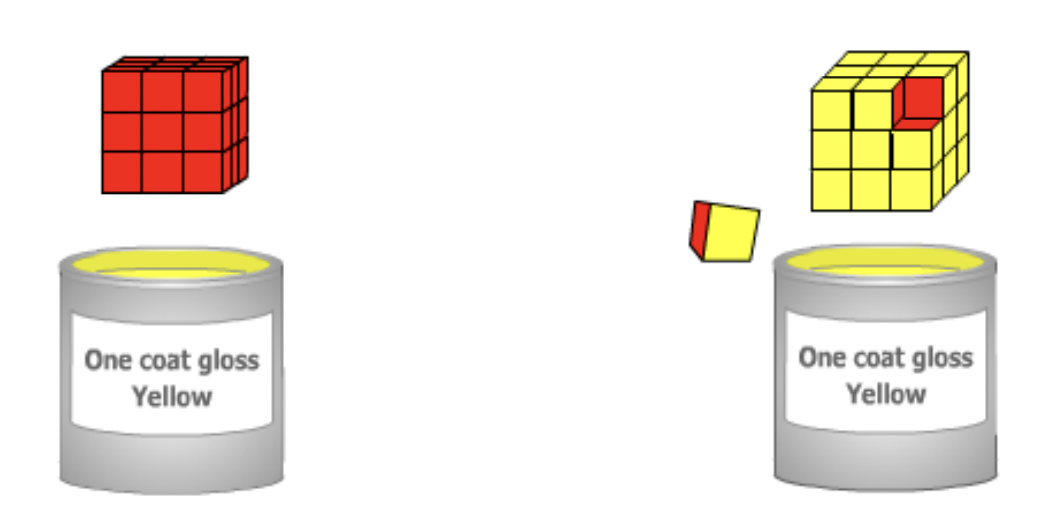
Cub pintat, de NRICH — NRICH. *Cub pintat*

Aquest problema, que es pot trobar analitzat amb més profunditat al bloc Variable, en referència amb el saber #ALG.ID.E, és interessant perquè es pot abordar numèricament i algebraicament i per la importància de com anar recollint i organitzant la informació per tal de descobrir els patrons. Tot seguit es poden veure dos exemples de com dos grups d’alumnes van anar treballant el problema. En el primer cas, va costar una mica més descobrir-ne la pauta; en el segon, el fet d’organitzar les troballes en una taula va facilitar molt l’obtenció de la pauta. Quan ens trobem amb situacions com aquesta a classe, val la pena comentar totes les possibilitats de resolució que hagin sortit per tal que l’alumnat pugui conèixer múltiples formes de representar la informació i, donada una situació, hi cerqui la més eficient.

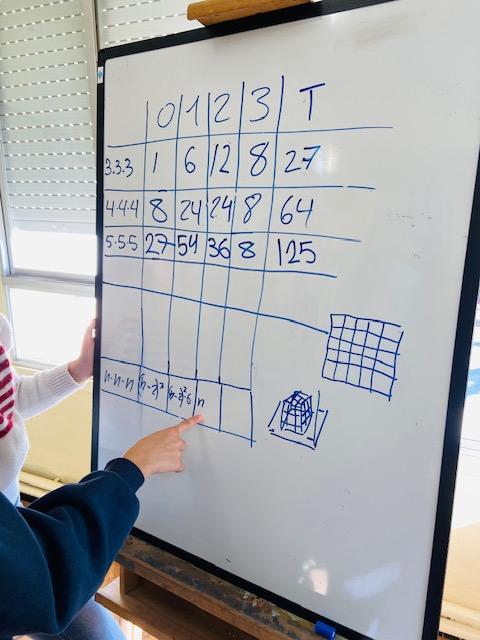Font: Núria Serra

Al Fem Matemàtiques del 2015 hi va sortir una versió d’aquest problema, el Cub foradat. La idea és la mateixa, però traient el cub central de cada cara:

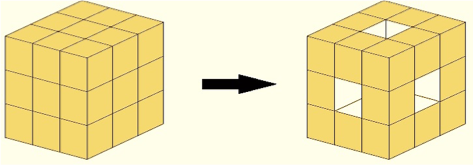
Font: Cub foradat, del Fem Matemàtiques — Fem Matemàtiques. *Cub foradat*

En el banc de recursos del web de l’ABEAM trobem l’entrada Cubs foradats. A més de l’enunciat complet del problema també hi ha una fitxa on s’explica per què és interessant el problema i es comenten molt detalladament estratègies de resolució.

Prova Cangur i Problemes a l’esprint

També per treballar el saber #2.ALG.PA.A, es vol fer esment d’altres concursos que poden esdevenir una gran font d’idees, no només per a 2n d’ESO, també per als altres cursos, i on podem trobar molta varietat de propostes. Començarem parlant de la Prova Cangur, activitat que cada any mobilitza milers d’infants i joves. Alguns exemples de les activitats proposades relacionades amb patrons són les següents:

I el concurs Problemes a l’esprint és una altra de les activitats que engresquen l’alumnat a resoldre reptes matemàtics, ara, però, col·laborativament, treballant en equip. S’hi poden trobar propostes com les següents:

Patrons generadors

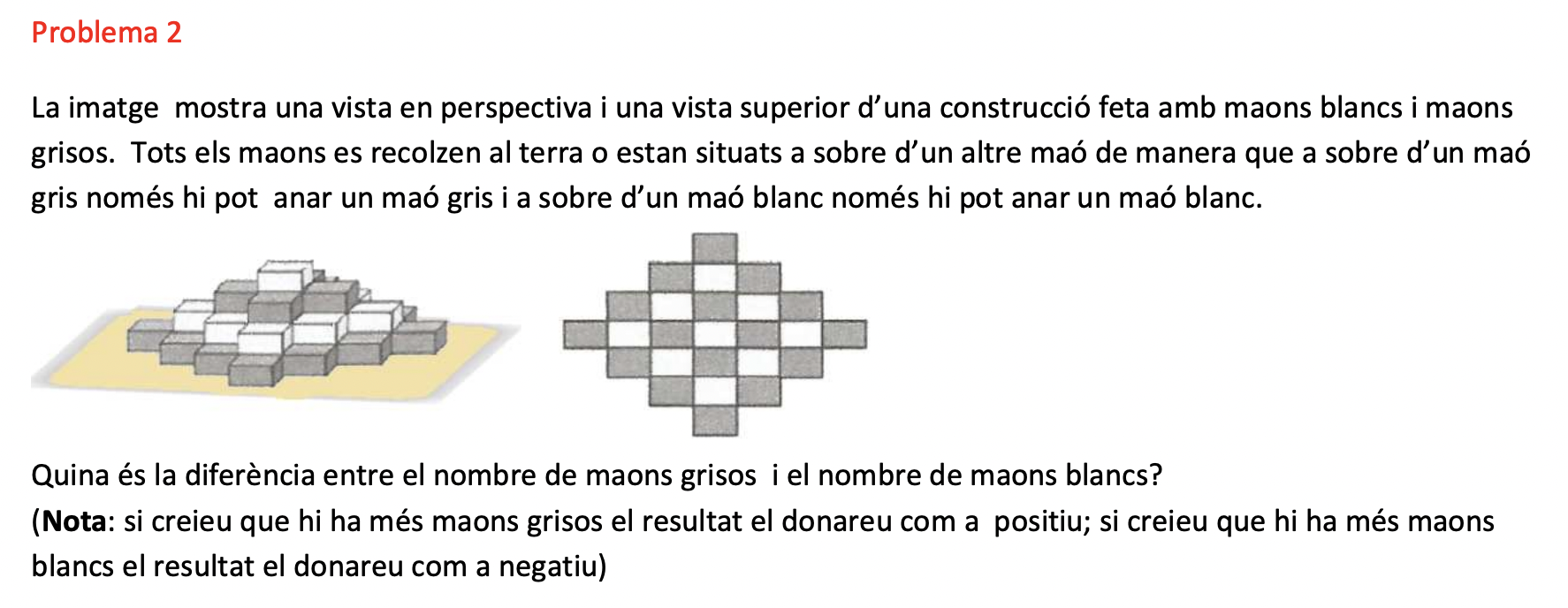
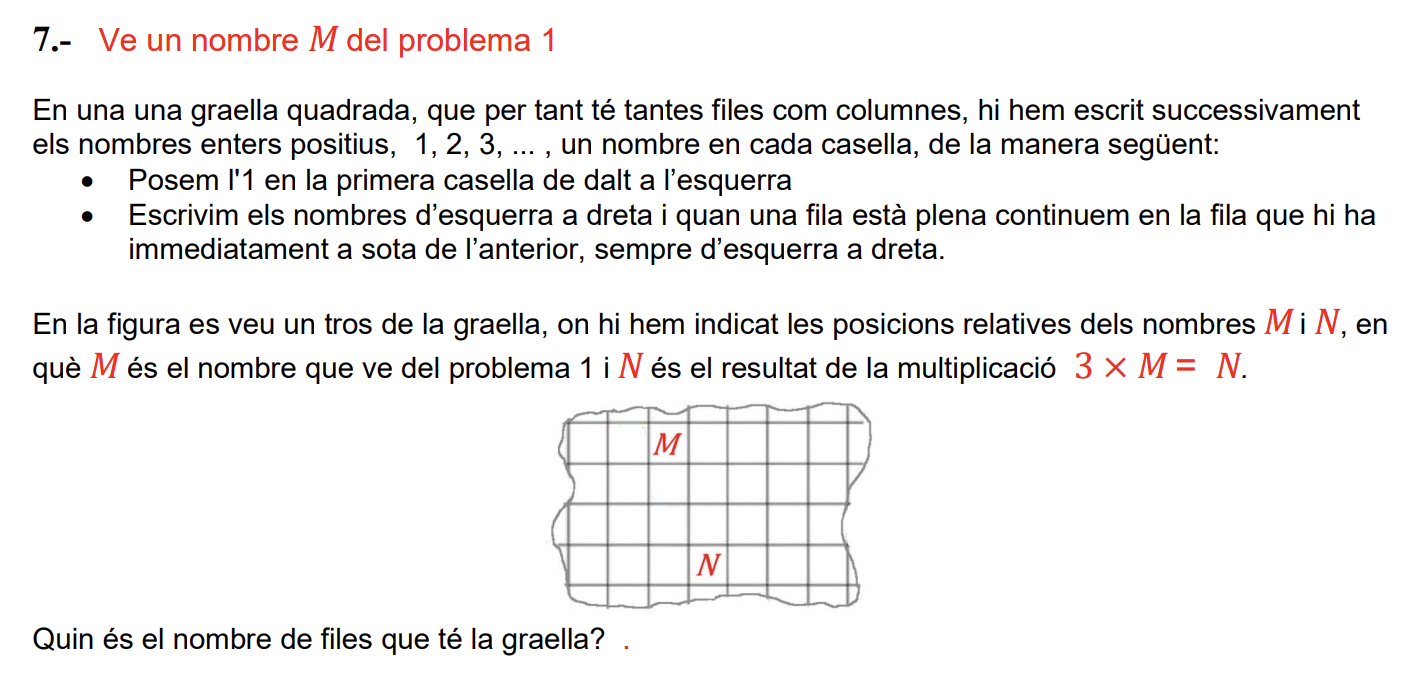
Un tipus d’activitats interessants són els problemes inversos, en els quals donada l’expressió de la generalització s’han de construir patrons generadors. Al bloc de l’escola Sadako podem veure com es poden portar a l’aula. És interessant veure com una mateixa expressió algebraica pot venir de diferents situacions geomètriques.

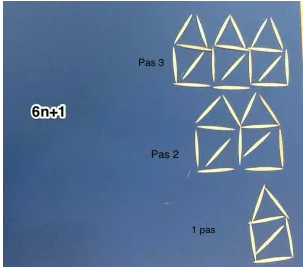
Cal recordar que el saber #2.ALG.PA.A és essencial, però que els recursos que s’acaben de descriure són només una proposta.

B. Observació de regularitats en diferents contextos matemàtics que permetin extreure conclusions o descobrir propietats.

Pràctica productiva: equacions de 1r grau

Per treballar el saber #2.ALG.PA.B proposem com a exemple l’activitat Pràctica productiva: equacions de 1r grau esmentada també al bloc Igualtat i desigualtat d’aquest mateix curs ( #ALG.ID) i que es pot trobar al web del PuntMat.

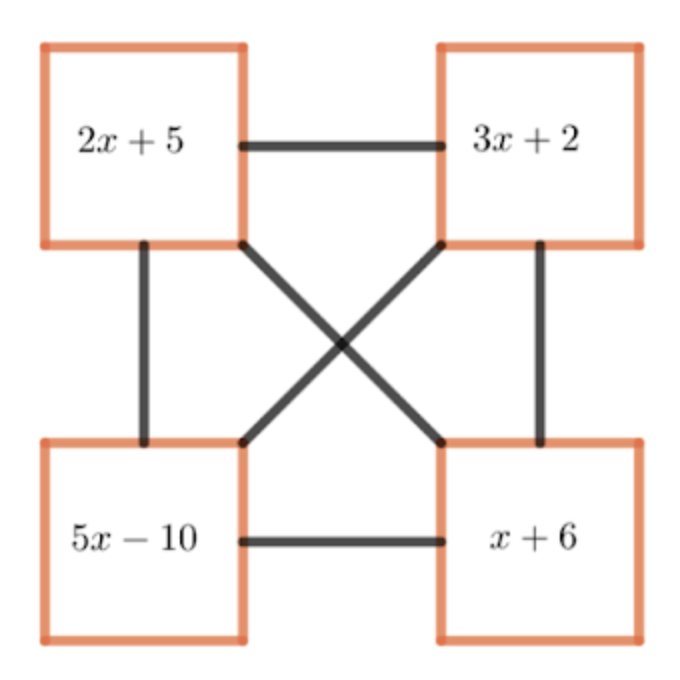
L’alumnat aprèn a resoldre equacions i, a continuació, cal que practiquin. Aquestes activitats proposen posar el focus en la cerca de patrons i regularitats i l’establiment de conjectures, a més de posar en pràctica les destreses apreses per resoldre les equacions.

Els dos primers exemples que se’ns mostren al web del PuntMat s’inspiren en la proposta de @colinfoster77 a Expression Polygons i, el tercer exemple, en la proposta d’@openmiddle Solving Equations with Variables on Both Sides.

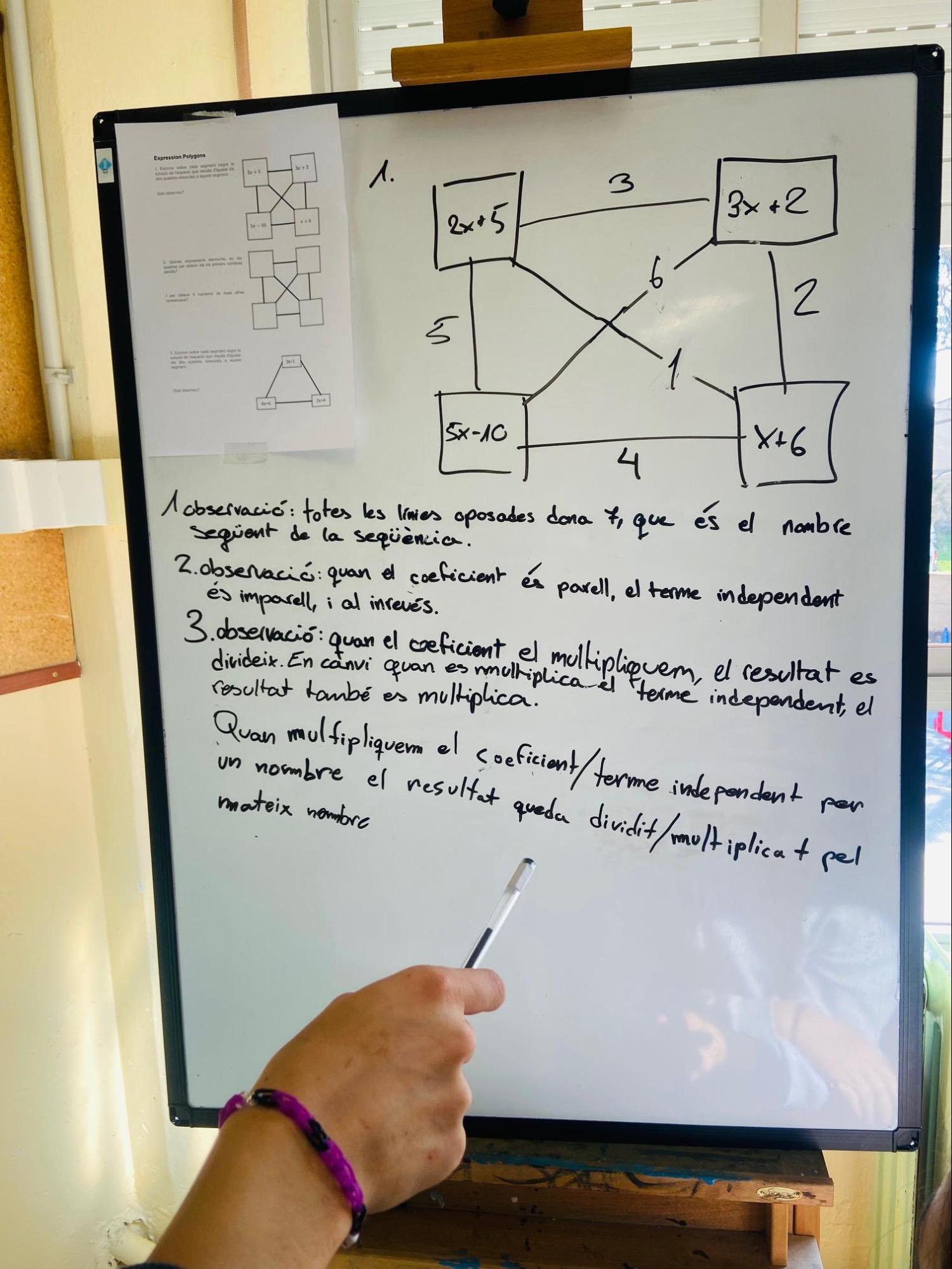
Pot resultar interessant veure el vídeo de la primera sessió de la formació Activitats riques i competències matemàtiques a l’aula de secundària organitzada pel CREAMAT ‒i que es va portar a terme el mes de juny de l’any 2020. Al vídeo es pot veure com les professores Cecília Calvo i Laura Morera fan una anàlisi d’aquesta activitat, donen idees per portar a l’aula, proposen preguntes interessants i fan aportacions de com estirar-la.

Comptem cares, arestes i vèrtexs.

La característica d’Euler relaciona el nombre de vèrtexs, cares i arestes dels poliedres. Es proposa descobrir aquesta relació a partir de la investigació amb diferents políedres i així connectar el treball de cerca de patrons i regularitats amb el treball del sentit espacial. Es pot trobar una referència a aquesta activitat al bloc Figures geomètriques d’aquest mateix curs ( #ESP.FG), dins de les propostes del Sentit espacial.

A la campanya Laboratori de matemàtiques del CREAMAT s’explica una proposta per treballar la característica d’Euler a l’aula, titulada Comptem cares, arestes i vèrtexs.

Es pot començar demanant a l’alumnat que construeixi diferents poliedres d’un mateix tipus, amb l’ajuda de material, com ara polígons encaixables; per exemple, prismes. Els poden construir amb base triangular, quadrada i pentagonal. Se’ls demana que en comptin les cares. Abans de construir-ne un altre amb base hexagonal, se’ls pregunta si poden saber quantes cares tindrà i després comprovar-ho (si es disposa de peces hexagonals o d’algun model de prisma hexagonal amb un altre material). A continuació es fa una taula per tal que, a partir de l’observació, puguin predir la quantitat de cares de qualsevol prisma i demanar una descripció de com ho calculen i per què ho calculen així.

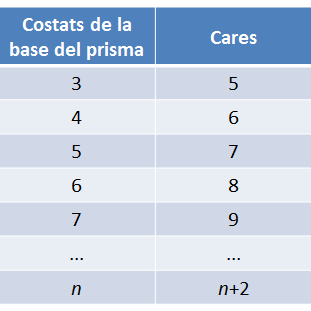
Després, es demana un recompte semblant amb les arestes. L’objectiu també és buscar una pauta.

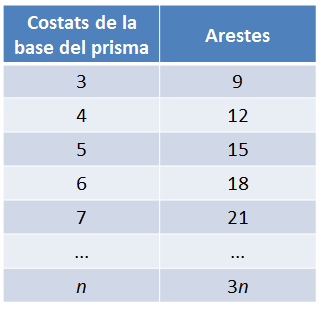
Finalment, es compten els vèrtexs. Sempre és important que expliquin l’argumentació de la manera de comptar ràpidament que apliquin, tot animant-los a no comptar els vèrtexs (o les cares, o les arestes) d’un en un.

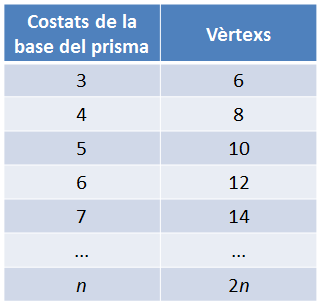
A continuació, es pot fer una feina semblant amb antiprismes. S’ha de guiar l’alumnat a observar que de cada costat de cada base en surt un triangle.

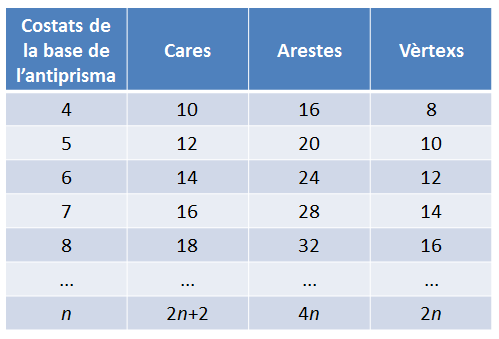
De manera anàloga es pot treballar amb els poliedres que calgui: amb piràmides, bipiràmides, poliedres regulars, prismes amb una piràmide a sobre, etc. Només cal mirar que siguin convexos. Si es van recollint dades, es poden fer taules molt completes que recullin, ara sí, només les quantitats de cares, arestes i vèrtexs.

A partir de l’observació i la comparació es busquen regularitats. Podem fer preguntes que portin l’alumnat cap allà on volem. Per exemple: Hi ha sempre més arestes que cares? Més arestes que vèrtexs? Més vèrtexs que cares? S’observa que les arestes «sempre guanyen». Que de vegades hi ha més cares que vèrtexs (prismes), de vegades més vèrtexs que cares (antiprismes) i de vegades la mateixa quantitat (piràmides).

Però, què està passant? Tal com es proposa des del PuntMat (Cecilia Calvo i David Barba) i des d’on el CREAMAT va agafar tot aquest itinerari, si les cares i vèrtexs «fan un equip», es veu que sempre guanyen… i que sempre guanyen per la mateixa diferència: dos. I aquí haurem trobat la característica d’Euler:

Cares + Vèrtexs = Arestes + 2

A partir d’aquí es pot investigar si aquesta propietat es compleix en qualsevol classe de poliedre.

Llicenciat sota la Llicència Creative Commons Reconeixement CompartirIgual 4.0