Recursos i activitats generals per al bloc de sabers
Una proposta per treballar el saber #4.NUM.QU.E a partir de la història ⎯saber #4.NUM.QU.A⎯ és la següent:
«El mètode d’Arquimedes per aproximar el valor de \(\pi\)»:
Arquimedes de Siracusa (287-212 aC) va desenvolupar una de les primeres aproximacions rigoroses del nombre \(\pi\) utilitzant mètodes geomètrics. Va aplicar un enfocament basat en polígons inscrits i circumscrits a una circumferència, la qual cosa va fitar el valor de \(\pi\) amb gran precisió. Aquest mètode s’explica en el vídeo Arquímedes y el Descubrimiento del número Pi.
L’objectiu d’aquesta proposta és que l’alumnat comprengui i sigui capaç d’aplicar el mètode d’Arquimedes per aproximar el valor de \(\pi\), tot reflexionant sobre com augmenta la precisió de l’aproximació a mesura que s’incrementa el nombre de costats dels polígons utilitzats.
Es recomana que l’activitat es dugui a terme en grups de \(3\) o \(4\) alumnes per fomentar la col·laboració i la discussió.
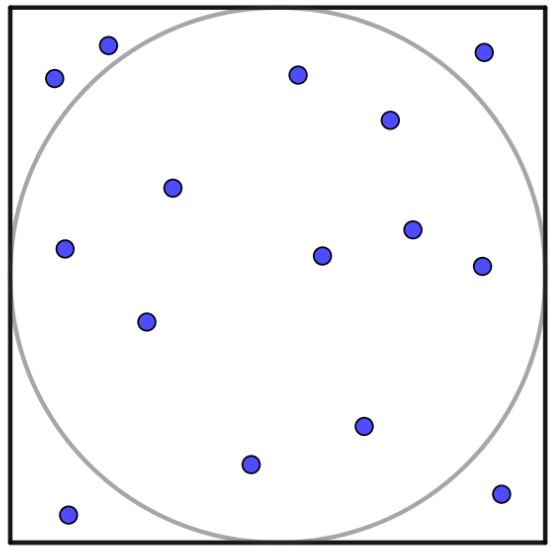
A partir d’una circumferència donada (manualment o mitjançant un programari com GeoGebra), cada grup ha de dibuixar:
- Un polígon regular inscrit.
- Un polígon regular circumscrit.
Es treballarà amb polígons de diferents nombres de costats (per exemple, \(6,\ 8\) i \(12\)).
Es demana que calculin:
- Els perímetres del polígon inscrit i del circumscrit.
- La mitjana dels valors dels perímetres obtinguts per aproximar el nombre \(\pi\):
\(\pi\approx\displaystyle\frac{\textrm{Perímetre del polígon inscrit + Perímetre del polígon circumscrit}}2\)
- Els errors absolut i relatiu.
Es fan les reflexions següents:
- Com afecta el nombre de costats dels polígons a la precisió de l’aproximació de \(\pi\)?
- Quines limitacions té el mètode d’Arquimedes i com es poden superar amb eines modernes?
- Per què és significatiu aquest mètode en la història de les matemàtiques?
Una ampliació de l’activitat és utilitzar GeoGebra per treballar amb polígons de més costats (\(48,\ 96\), o més). Això permet comprovar la precisió del mètode d’Arquimedes amb més detall i obtenir gràficament la convergència del valor de \(\pi\).
Una altra activitat per treballar els sabers #4.NUM.QU.A i #4.NUM.QU.E fa referència a Ramon Llull i la quadratura del cercle:
Al web del CESIRE hi ha publicada l’entrada Llull i les matemàtiques (II): La quadratura del cercle, en què s’explica com Llull aborda la quadratura del cercle:
Es pot traslladar a l’aula el mètode utilitzat per Llull seguint els cànons de la geometria clàssica:
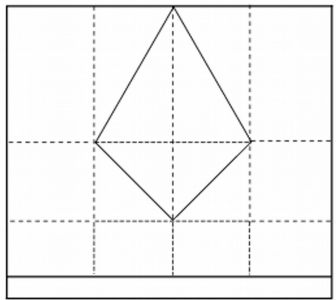
Llull proposa dibuixar els quadrats inscrit i circumscrit a una circumferència.
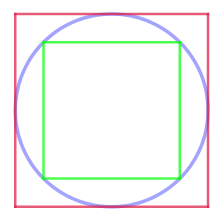
Font: Llull i les matemàtiques (II): La quadratura del cercle
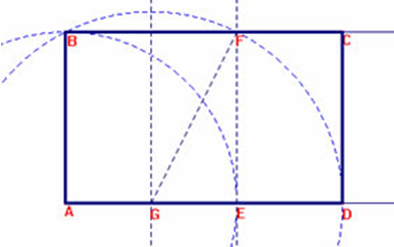
Tot mesurant el costat dels dos quadrats, calculava el costat d’un quadrat nou que tingués com a mesura del costat la mitjana dels altres dos.
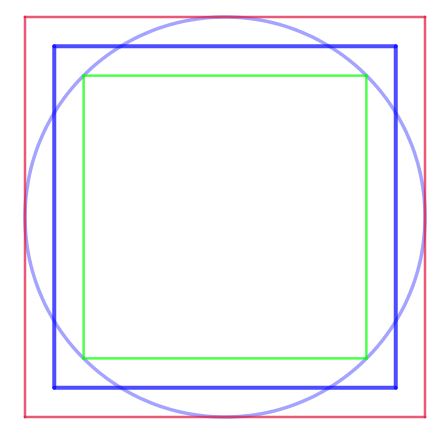
Font: Llull i les matemàtiques (II): La quadratura del cercle
Segons Llull, aquest quadrat, l’àrea del qual era més gran que la del quadrat inscrit però més petita que la del circumscrit, coincidia amb l’àrea del cercle.
El mètode es podia aplicar també a altres polígons, com el triangle.
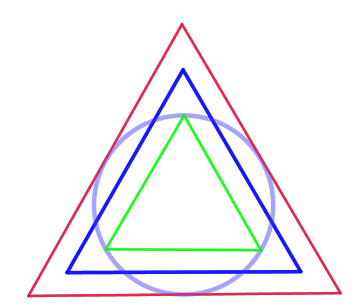
Font: Llull i les matemàtiques (II): La quadratura del cercle
Després de realitzar la construcció, es pot plantejar a l’alumnat la següent pregunta: «És certa aquesta afirmació? Si no ho és, quin és l’error?»
Per investigar les proporcions entre les àrees, es pot utilitzar una eina com el Geogebra.
Com a curiositat, es pot veure, a la tomba de Llull, una escultura que fa referència a la quadratura del cercle:

Font: diari Ara Balears
La construcció i ús d’una corda Pitagòrica és una activitat vivencial que permet treballar els sabers #4.NUM.QU.A i #4.NUM.QU.C.
Aquesta proposta, inspirada en l’època pitagòrica, explora la descoberta dels nombres irracionals mitjançant l’ús d’una corda de Pitàgores, una eina senzilla i pràctica que permet construir triangles rectangles de dimensions precises, aprofitant la propietat fonamental del teorema de Pitàgores.
La corda de Pitàgores es basa en un conjunt de nombres enters que compleixen la relació: \(a^2+b^2=c^2\) en què \(a,\ b\) i \( c\) són els costats del triangle rectangle (ternes pitagòriques).
Per construir-la, caldrà:
- Una corda o cordill flexible, però no elàstic.
- Marcadors, com ara nusos, llaços, cintes o anelles.
Primer de tot cal mesurar i marcar segments d’igual longitud a la corda. Cada segment representarà una unitat.
A continuació es representaran triangles rectangles amb diferents ternes pitagòriques.
Per exemple, per representar el triangle de costats \(3,\ 4,\) i \(5\):
- Es trien els primers \(3\) nusos per al primer costat.
- Els següents \(4\) per a l’altre costat.
- Els \(5\) per al tercer costat del triangle.
S’uneixen els extrems corresponents per formar un triangle rectangle i s’observa que l’angle recte està entre els dos costats més curts.
Es repeteix el procediment amb altres ternes pitagòriques. D’aquesta manera, s’aprofundeix en la comprensió del teorema de Pitàgores i la seva representació amb la corda.
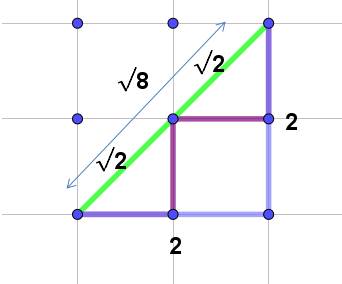
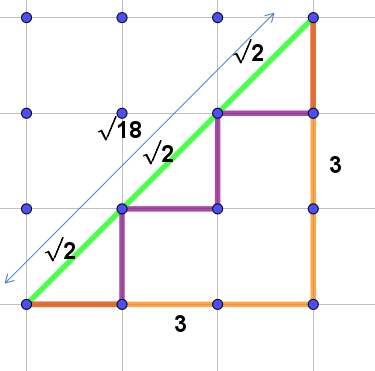
Una vegada s’ha entès com cal utilitzar la corda, es pot fer servir per representar nombres irracionals com ara \(\sqrt{2},\ \sqrt{3},\ \sqrt{5},\) etc., construint els triangles rectangles corresponents:
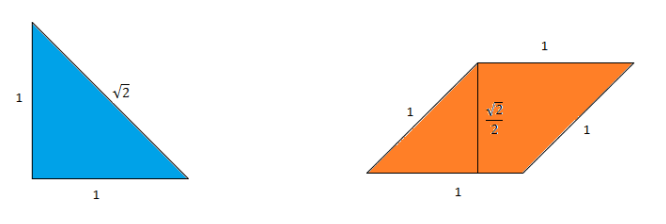
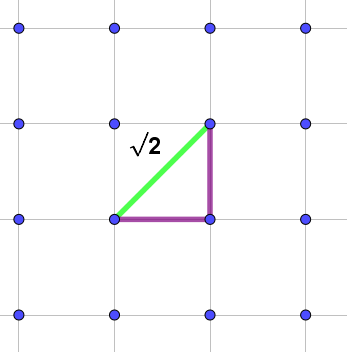
- Per representar \(\sqrt{2}\), es construeix un triangle rectangle amb els dos catets de longitud \(1\) unitat cadascun. La hipotenusa del triangle serà \(\sqrt{2}\).
- Per a \(\sqrt{3}\), es construeix un triangle rectangle amb un catet d'\(1\) unitat i l’altre catet de \(\sqrt{2}\).
- Continua aquest procés per representar altres nombres irracionals.
Recursos i activitats per treballar sabers concrets
A continuació, es presenten algunes idees sobre recursos i activitats d’aprenentatge que poden contribuir a l’adquisició dels sabers d’aquest bloc.