La mida de les peces
Una bona activitat per treballar la interpretació dels resultats d’un estudi i relacionar-los amb els seus objectius, saber #3.EST.IN.H, és treballar en contextos com ara el màrqueting, la producció, la logística i la gestió empresarial. El grup Vilatzara, a l’activitat La mida de les peces fa una proposta d’activitat on s’han d’escollir dues màquines per a la producció de peces i amb la complexitat que totes dues tenen les mateixes característiques tècniques i costen el mateix. Per això s’ha decidit fer-los una prova construint amb cada màquina sis peces i així mesurar l’amplada de cada peça fabricada.
Quan es fa l’estudi de les dades, s’arriba a la conclusió que totes dues màquines produeixen peces que tenen la mateixa mitjana, i caldrà fer una sèrie de preguntes i activitats que portin a reflexionar l’alumnat sobre la importància de la variabilitat i la consistència en els resultats per treballar també així el saber #3.EST.DI.H.
Us proposem les preguntes següents per a la interpretació de les dades i perquè l’alumnat acabi discriminant quina màquina és l’adequada tenint en compte el corresponent càlcul de la desviació:
Comprensió de la mitjana:
- Què significa que dues màquines tinguin la mateixa mitjana? Quins resultats concrets esperaries de cada màquina?
- Si la mitjana de les peces produïdes per les dues màquines és la mateixa, vol dir que les dues màquines són iguals en qualitat o rendiment?
Aquestes preguntes ajuden els alumnes a adonar-se que la mitjana només descriu una tendència central, però no captura la variabilitat en les dades.
Introducció a la variabilitat:
- Imagina que observes que una de les màquines produeix algunes peces molt per sobre de la mitjana i altres molt per sota. Com creus que això afectaria la qualitat del procés?
- Què passaria si una altra màquina produeix peces gairebé idèntiques en cada passada? Quina màquina consideraries més consistent?
Aquestes preguntes poden dur els estudiants a reconèixer que, tot i que les dues màquines poden tenir la mateixa mitjana, la dispersió dels resultats (la variabilitat) pot ser molt diferent.
Importància de la dispersió:
- Si tinguéssim dues màquines amb la mateixa mitjana, però una té molta més variabilitat que l’altra, quina màquina consideraries millor per a un procés de producció on la precisió és important?
- Per què creus que és important conèixer no només la mitjana, sinó també quanta variabilitat hi ha en els resultats?
Aquestes preguntes poden portar l’alumnat a pensar en la importància de mesurar no només la mitjana dels resultats, sinó també com es distribueixen al voltant d’aquesta.
Desviació mitjana com a eina de mesura:
- Si volguéssim comparar la consistència entre les dues màquines, quina mesura creus que podríem utilitzar per saber quina té més estabilitat en els seus resultats?
- Com creus que podem calcular la fiabilitat d’un procés de producció?
Aquestes preguntes guien l’alumnat cap a la idea que la desviació mitjana és una mesura que pot ajudar a quantificar la variabilitat i la consistència dels resultats, aspectes que no es reflecteixen només amb la mitjana.
Dificultats en el càlcul de la desviació mitjana o desviació estàndard
- Com podríem evitar que les desviacions positives i negatives es cancel·lin entre elles quan les sumem?
- Si volguéssim obtenir una mesura que indiqués l’efecte mitjà de les desviacions respecte a la mitjana, què podríem fer amb aquestes desviacions?
- Com podríem calcular una mena de mitjana de les desviacions?
- Quines dificultats comporta fer valors absoluts? Per què sembla més pràctic fer quadrats?
- Què passaria si, en lloc de sumar les desviacions directament, les elevéssim al quadrat per evitar que es cancel·lin? Què ens aportaria això? Com es modificarien les unitats de mesura en elevar al quadrat? Què podem fer per tenir les unitats de mesura correctes?
La durada de les piles
En la mateixa línia, el grup Vilatzara també proposa l’activitat La durada de les piles, en què una cooperativa de ferreteries rep dues ofertes de dos fabricants diferents per a un mateix model de pila.
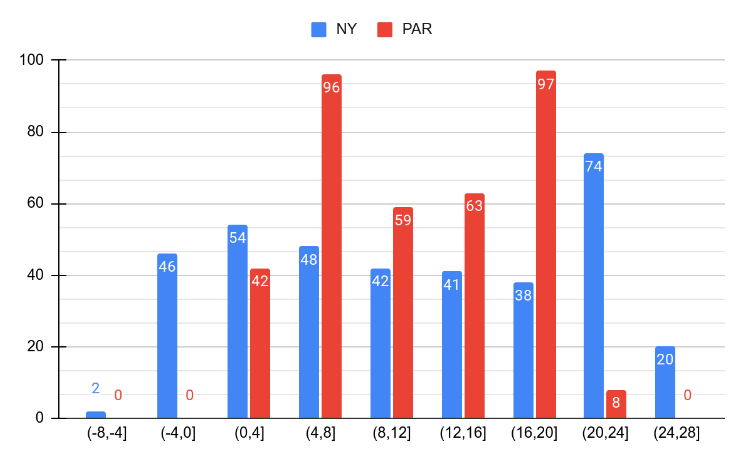
Les piles dels dos fabricants costen el mateix. Per tant, el preu no és un factor decisiu i altre cop la durada de les dues piles presenta la mateixa mitjana, la qual cosa les fa pràcticament equivalents. Si es representen les freqüències en un diagrama de barres ja es veu que no ho són tant, d’equivalents, i aquesta diferència es quantifica amb la desviació (en aquest cas, poc importa si es tracta d’una desviació mitjana o d’una d’estàndard). Convé interpretar la poca dispersió com una mesura de la regularitat o la fiabilitat del producte. L’objectiu és aplicar el càlcul de la desviació per complementar la informació del paràmetre de centralització i escollir la cooperativa més adient.
Partint de l’activitat de la durada de les piles del grup Vilatzara podem treballar el saber #3.EST.IN.H, tot dissenyant un estudi estadístic per comparar la duració de diverses marques de piles i determinar quina ofereix més bon rendiment respecte al preu. Per portar a terme la nostra investigació, necessitarem piles de diferents marques, dispositius que consumeixin energia de manera constant com llanternes led, joguines electròniques, ràdios petites, etc. i un cronòmetre o una càmera per registrar el temps d’ús.
Registrant el temps total de funcionament i repetint el procés amb totes les piles de cada marca, podem calcular la mitjana de duració de les piles de cada marca, la desviació estàndard per veure la variabilitat entre piles de la mateixa marca i el coeficient de variació per comparar la dispersió entre marques.