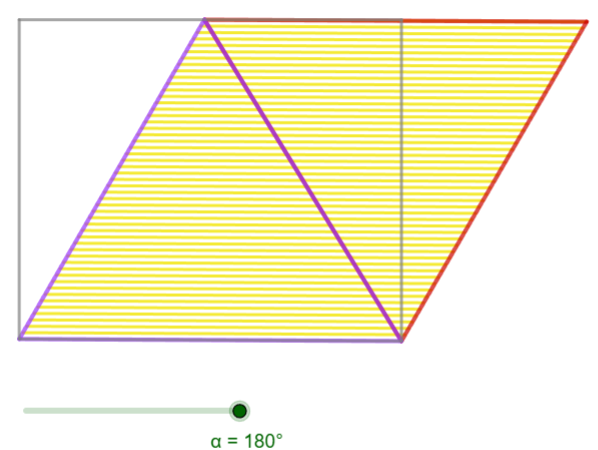
Reflexions generals
L’activitat matemàtica sobre el sentit de la mesura a 1r d’ESO se centra en aquest conjunt de sabers. És important que l’alumnat visqui situacions de mesurament, ja siguin de mesura directa, a partir de l’elecció d’instruments de mesura o fent comparacions amb la unitat patró escollida; o de mesura indirecta, en què mitjançant l’obtenció d’unes determinades magnituds i aplicant les operacions adients entre elles, s’acaba obtenint la mesura desitjada. En aquestes situacions es treballaran indubtablement sabers que pertanyen als altres dos blocs, Magnitud i Estimació i relació, i és recomanable que sigui així. Mesurar implica comparar i, com a conseqüència, ordenar i reconèixer els diferents ordres de magnitud que es poden donar. A més a més, cal oferir a l’alumnat moltes experiències de mesurament de diferents magnituds per tal d’anar millorant les seves estimacions.
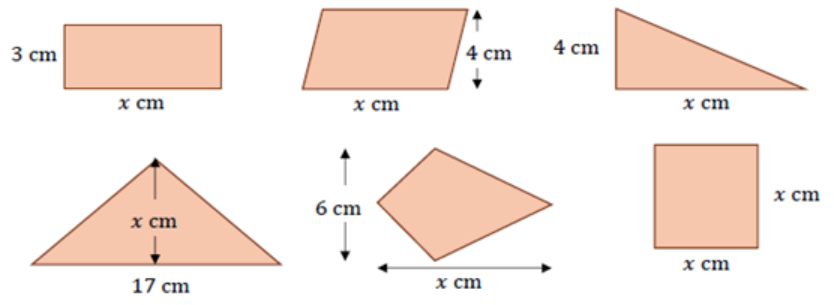
Durant la primària el càlcul de mesures directes ha estat fonamental, i en els darrers cursos han començat a aparèixer situacions de mesures indirectes: càlcul d’àrees de quadrats o perímetres de polígons a partir de la mesura dels seus costats. El pas de l’una a l’altra s’ha de cuidar, i és precisament a primer de secundària on tenim una oportunitat perquè les diferents expressions de càlcul de mesures que apareguin siguin una descoberta per a l’alumnat i no pas un conjunt de fórmules descontextualitzades.
Es recomana afavorir el treball en grups heterogenis d’unes tres persones, amb l’objectiu de promoure la conversa matemàtica, compartir conjectures i prendre decisions consensuades i fonamentades en el raonament. Tanmateix, cal dedicar estones al treball individual i educar l’alumnat a enfrontar-se als problemes per tal que aquests esdevinguin reptes personals i no limitadors d’aprenentatge.
Comentaris sobre les connexions
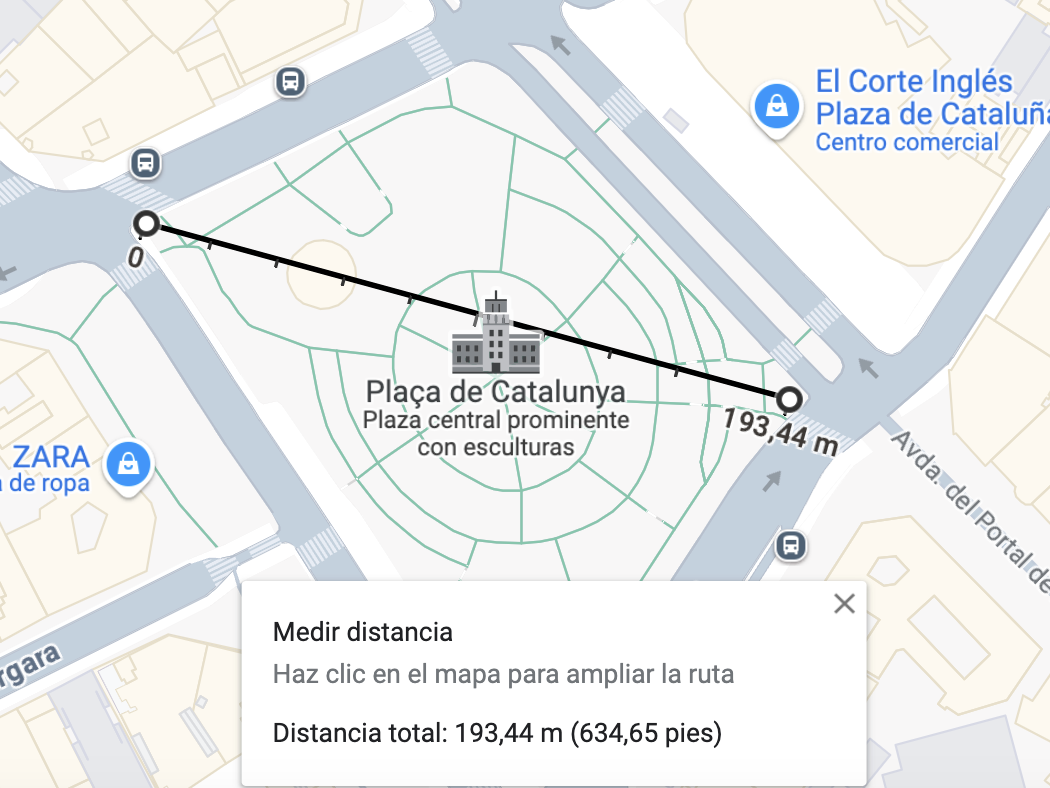
A l’hora de proposar activitats de representació a escala i fitament d’objectes s’establirà una connexió amb el bloc de sabers de raonament proporcional, pertanyents al sentit de numeració. Seran propostes lligades a l’elaboració de plànols, a la seva lectura o a l’ús d’eines digitals, com OpenStreetMap o Google Maps, per tal d’obtenir algunes distàncies, superfícies, etc.
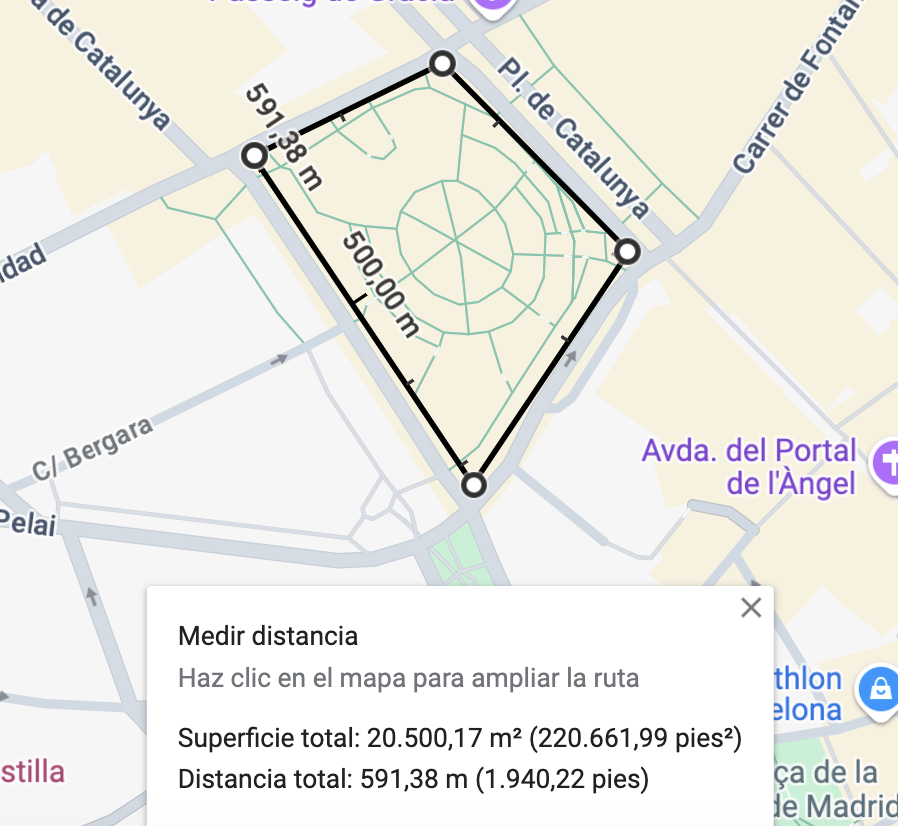
Font: Elaboració pròpia
Comprendre l’escala com una raó de proporcionalitat i saber-la emprar correctament permetrà una bona lectura de mesures en mapes i la seva traducció a la realitat. És important evitar l’ús d’estratègies de càlcul o algorismes que no incorporin un raonament. Per això recomanem usar les taules de proporcionalitat que permetran veure en tot moment la relació d’equivalència existent entre dues magnituds. Si s’escau, es pot aprofitar per relacionar aquesta taula amb els resultats que s’obtenen aplicant «la regla de tres», amb l’equació de proporcionalitat o en el càlcul de percentatges quan es multiplica amb un tant per u. En aquestes situacions podem aprofitar per treballar amb eines tecnològiques com la calculadora i el full de càlcul. Cal insistir en aquestes situacions sobre representacions proporcionals (figures semblants) i buscar que l’alumnat mateix identifiqui quines magnituds es mantenen invariants (magnituds angulars) i quines es modifiquen i de quina manera. La consolidació d’aquests sabers, sempre presentats en context, seran el punt de partida de nous escenaris en cursos posteriors estretament lligats als sentits de mesura i espacial.
Tal com s’ha observat en la concreció de sabers, en el bloc de mesurament sorgeixen moltes connexions amb el sentit algebraic. La necessitat que el mateix alumnat trobi estratègies per al càlcul de mesures indirectes ja sigui mitjançant el material manipulatiu, les aplicacions de geometria dinàmica o la descomposició de figures, farà que disposi de diferents recursos per solucionar un mateix problema, alhora que enfortirà el seu coneixement i les relacions entre diferents parts de la matemàtica. En moltes d’aquestes situacions caldrà desenvolupar un pla per resoldre-les, i el raonament matemàtic serà fonamental per dur-lo a terme. Sovint caldrà descompondre els problemes en parts més petites com a estratègia de resolució. És per això que hi veiem una clara connexió amb el pensament computacional. Si tot aquest procés es duu a terme en petits grups s’aconseguirà, a més a més, que hi hagi una construcció de coneixement compartida, una exposició d’idees per part de l’alumnat dins de cada grup i, com a conseqüència, una millora en la comunicació matemàtica, així com la possibilitat que aquestes idees es vegin confrontades amb altres i, per tant, es posaran en joc el raonament i l’argumentació.
L’ús de programes de geometria dinàmica per al mesurament de longituds i superfícies, i altres com el full de càlcul o simuladors virtuals en activitats lligades amb la mesura de la incertesa, requeriran una introducció al seu maneig, i per tant, també es treballaran sabers propis del pensament computacional.
Precisament, en situacions de mesura de probabilitat d’esdeveniments simples en experiments aleatoris apareix una connexió directa amb el sentit estocàstic, concretament amb el sabers propis de predictibilitat i incertesa.
No és fàcil desvincular el sentit de la mesura del sentit espacial. La connexió natural entre l’un i l’altre fa que en la gran majoria de propostes trobem lligams entre els seus sabers. Tanmateix, d’entre tots els que pertanyen al grup de mesurament, hem volgut destacar la descoberta de \(\pi\) com una raó entre magnituds d’elements propis de la circumferència i el cercle, com aquell que té una connexió més forta amb el sentit espacial, en particular, amb el conjunt de sabers propis de les formes geomètriques de dues i tres dimensions.
A part de les connexions internes comentades en aquest mateix apartat, no volem deixar d’esmentar les moltes connexions externes que s’esdevenen en situacions de mesurament:
- Selecció i bon ús d’instruments de mesura, alguns dels quals relacionats amb les ciències experimentals o amb la tecnologia.
- Creació i interpretació de plànols, mapes i figures a escala, relacionat amb el món del disseny, l’arquitectura i l’urbanisme.
- Realització d’activitats de mesura directa contextualitzades en un entorn proper de l’alumnat.
Observacions sobre alguns sabers d’aquest bloc
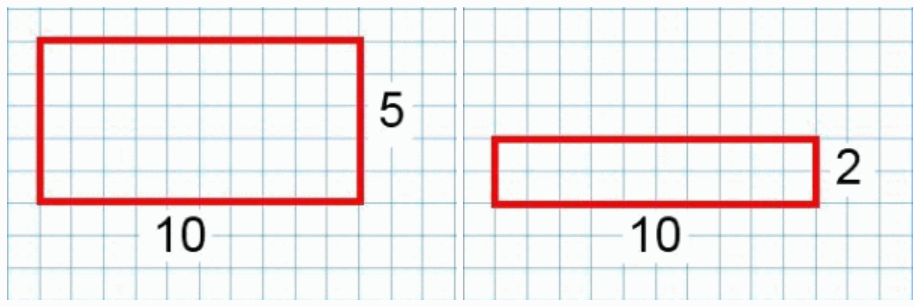
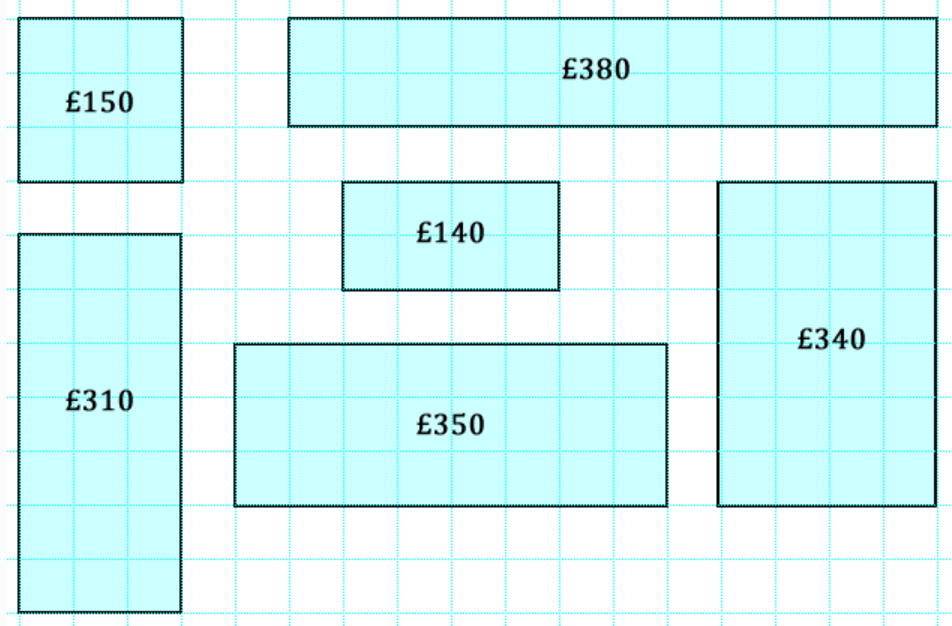
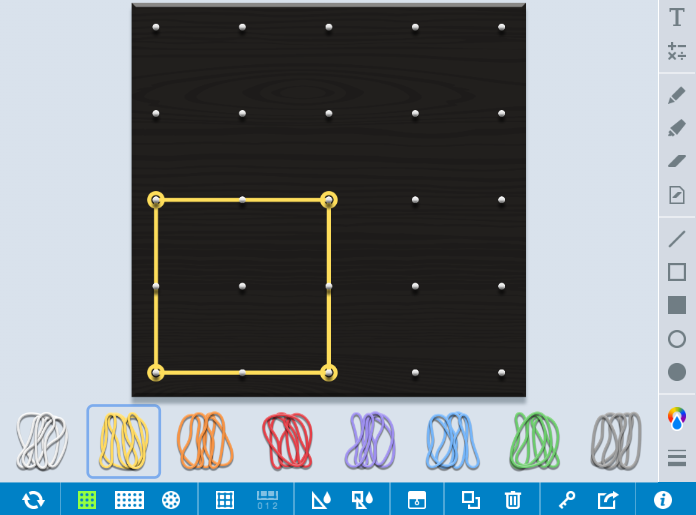
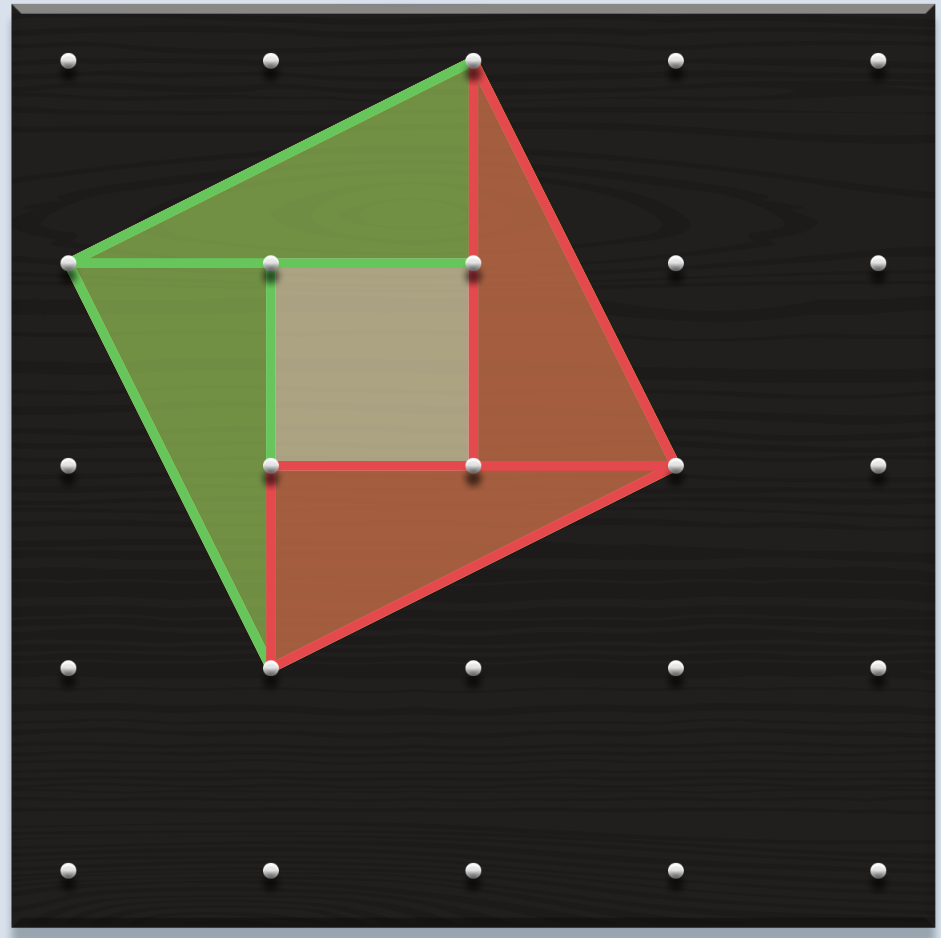
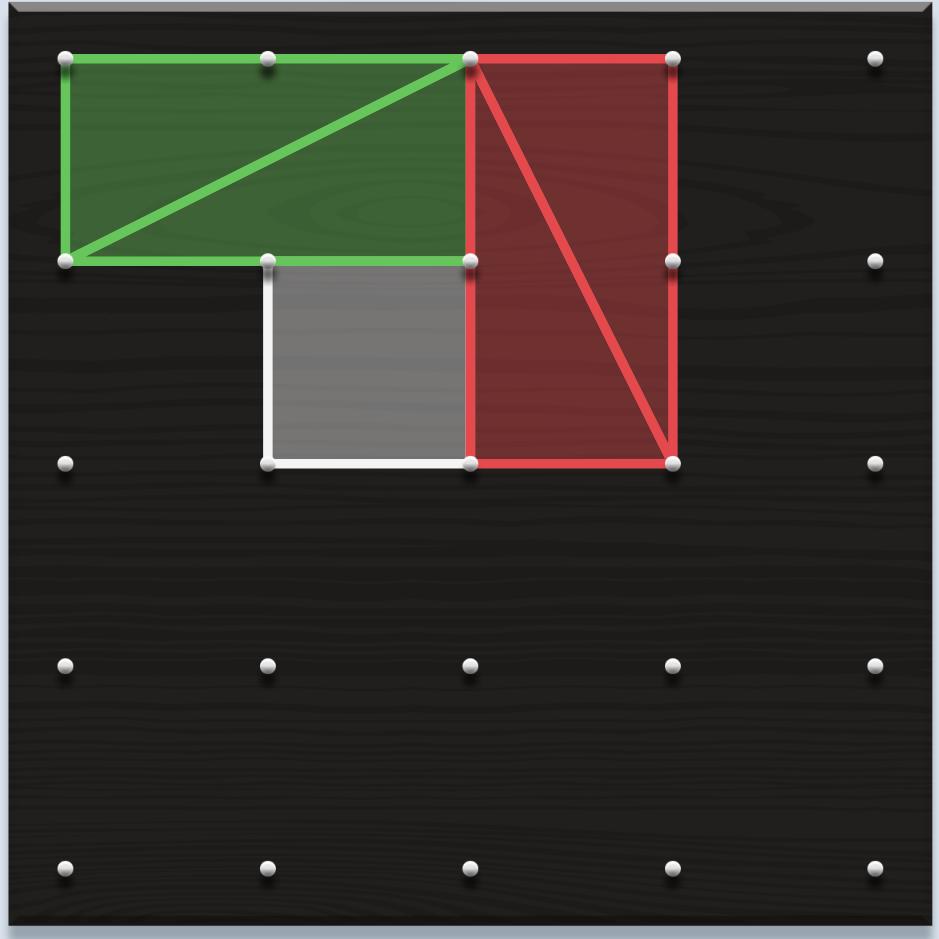
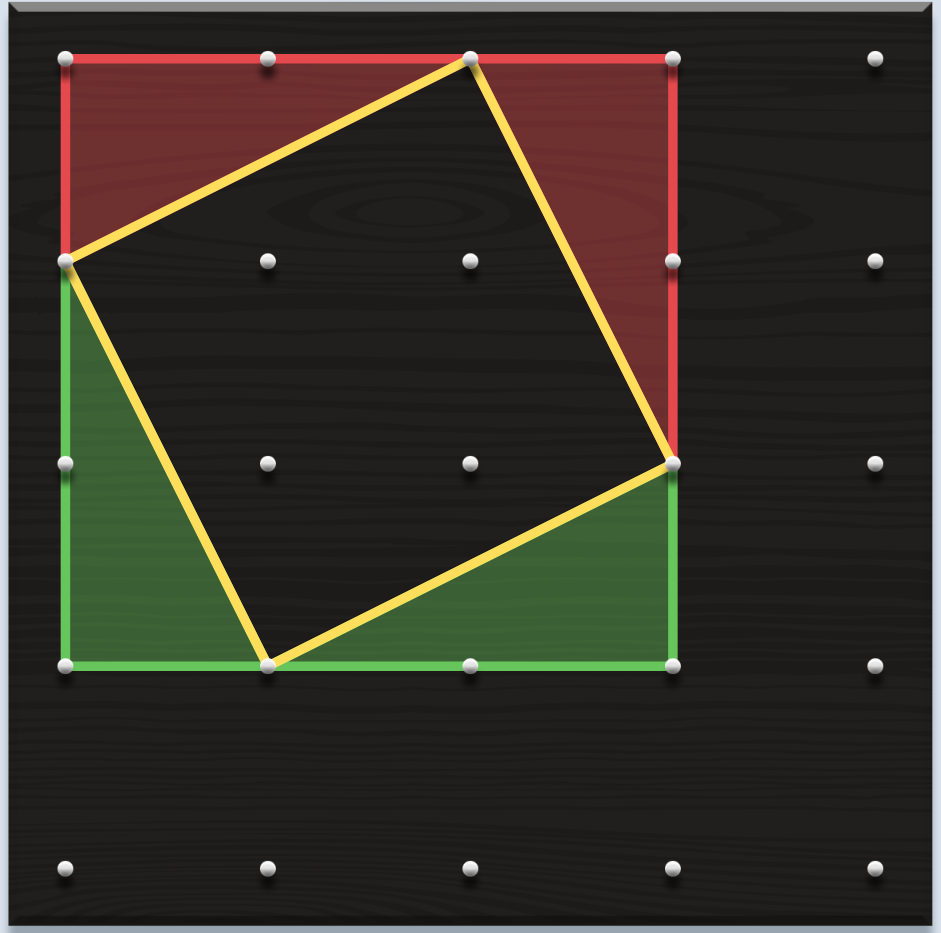
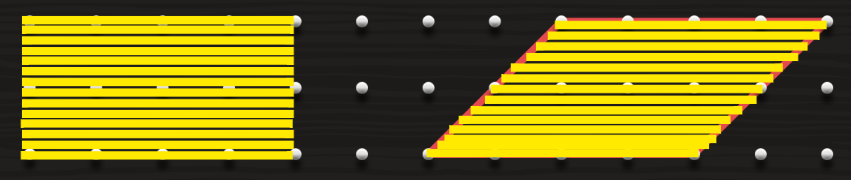
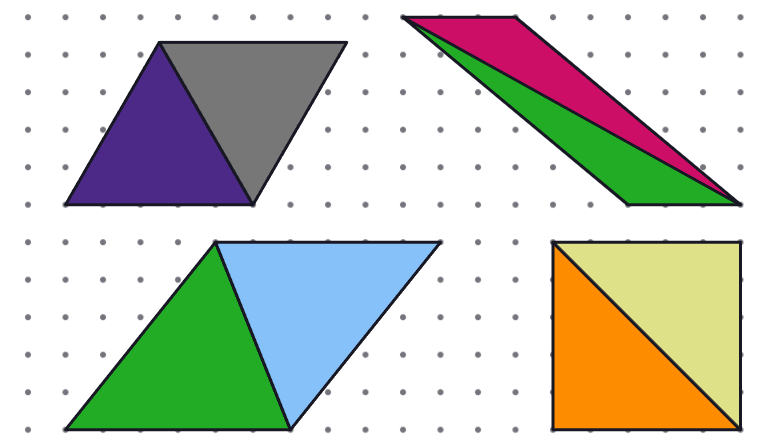
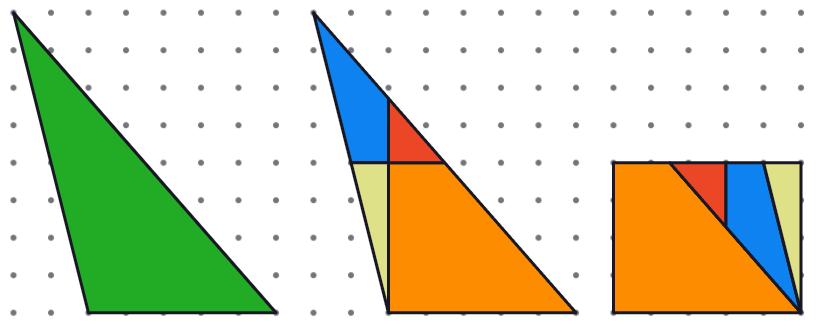
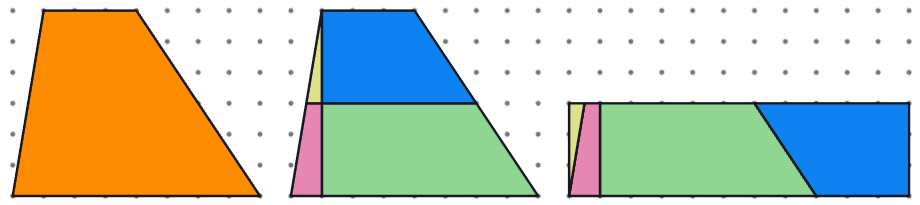
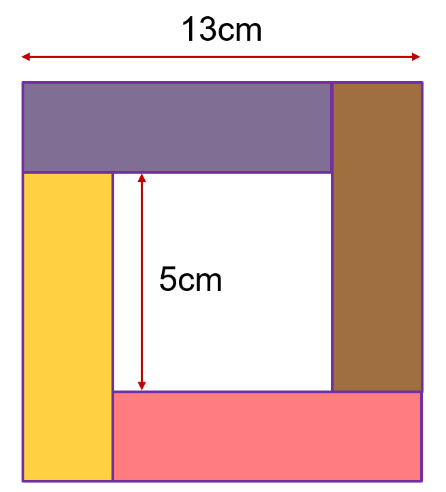
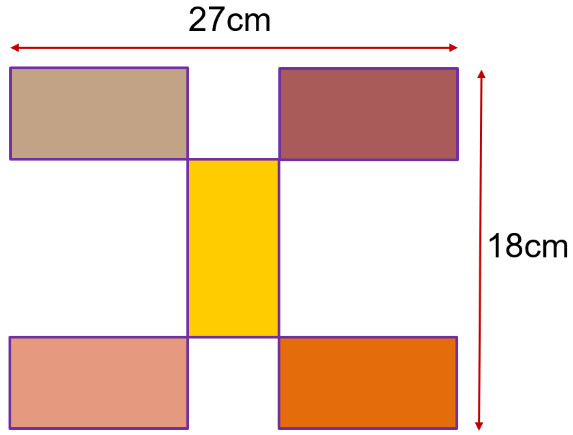
Una dificultat habitual entre l’alumnat és la confusió entre àrea i perímetre. També es dona entre volum i àrea quan passem al treball amb objectes en 3D. Aquesta dificultat ja s’identifica en cursos anteriors, a la primària, i s’accentua quan es fan activitats de mesurament a partir de l’aplicació de fórmules. És molt important, però, no avançar l’ús d’expressions algebraiques fins que no quedi clara la distinció d’una magnitud i l’altra, i es coneguin diferents estratègies per obtenir-les. Per tal de treballar el raonament, pot ser interessant presentar activitats que, mantenint fixada una de les magnituds –el perímetre, per exemple–, es vagi variant l’altra, en aquest cas, l’àrea. I a l’inrevés. Contraposar o fer intervenir alhora les dues magnituds en una mateixa activitat permetrà diferenciar-les, a la vegada que formaran part de les deduccions i raonaments que faci l’alumnat.
La naturalesa del saber #1.MES.ME.J, tal com s’ha concebut, permetria incloure’l tant en el bloc Mesurament com en el d’Estimacions i relacions. Darrere de la seva redacció hi ha una intenció metodològica. Recomanem que l’alumnat arribi a emprar la regla de Laplace a partir de la seva descoberta i comprensió. Aquesta idea sorgirà com a conseqüència de l’experimentació, on l’evolució de les mateixes freqüències relatives permetran observar com tendeixen a la mesura de probabilitat d’un esdeveniment. D’aquesta manera, el saber #1.MES.ME.J preveu la regla de Laplace, que serà un instrument per fer mesuraments, i les freqüències relatives, que seran una estimació de la probabilitat.
Comentaris sobre els sabers essencials i d’ampliació
Una dificultat habitual entre l’alumnat és la confusió entre àrea i perímetre. També es dona entre volum i àrea quan passem al treball amb objectes en 3D. Aquesta dificultat ja s’identifica en cursos anteriors, a la primària, i s’accentua quan es fan activitats de mesurament a partir de l’aplicació de fórmules. És molt important, però, no avançar l’ús d’expressions algebraiques fins que no quedi clara la distinció d’una magnitud i l’altra, i es coneguin diferents estratègies per obtenir-les. Per tal de treballar el raonament, pot ser interessant presentar activitats que, mantenint fixada una de les magnituds –el perímetre, per exemple–, es vagi variant l’altra, en aquest cas, l’àrea. I a l’inrevés. Contraposar o fer intervenir alhora les dues magnituds en una mateixa activitat permetrà diferenciar-les, a la vegada que formaran part de les deduccions i raonaments que faci l’alumnat.
La naturalesa del saber #1.MES.ME.J, tal com s’ha concebut, permetria incloure’l tant en el bloc Mesurament com en el d’Estimacions i relacions. Darrere de la seva redacció hi ha una intenció metodològica. Recomanem que l’alumnat arribi a emprar la regla de Laplace a partir de la seva descoberta i comprensió. Aquesta idea sorgirà com a conseqüència de l’experimentació, on l’evolució de les mateixes freqüències relatives permetran observar com tendeixen a la mesura de probabilitat d’un esdeveniment. D’aquesta manera, el saber #1.MES.ME.J preveu la regla de Laplace, que serà un instrument per fer mesuraments, i les freqüències relatives, que seran una estimació de la probabilitat.