Magnitud

Sabers

Identificació d’atributs mesurables en objectes matemàtics o físics, en el nostre entorn.
Establiment d’unitats patró de mesura (a partir del propi cos, unitats antropomètriques o d’objectes coneguts propers a l’alumnat) adequades a cada situació.
Comparació de les diferents unitats de mesura per a un mateix atribut.
Adquisició, per consens, d’una unitat de mesura de referència comuna.
Avaluació de la importància de l’establiment del sistema mètric decimal (naixement del metre).
Adequació de la unitat de mesura als atributs dels objectes.
Elecció d’unitats de mesura adients per poder operar entre elles i, si escau, per generar-ne de derivades (per exemple, 1 m × 1 m = 1 m2).
[ESS]

#NUM.SO
Determinació del grau qualitatiu de certesa o incertesa associat a esdeveniments: segur, molt probable, poc probable, possible, impossible…
[ESS]

#EST.PI

Descripció i orientacions

Reflexions generals

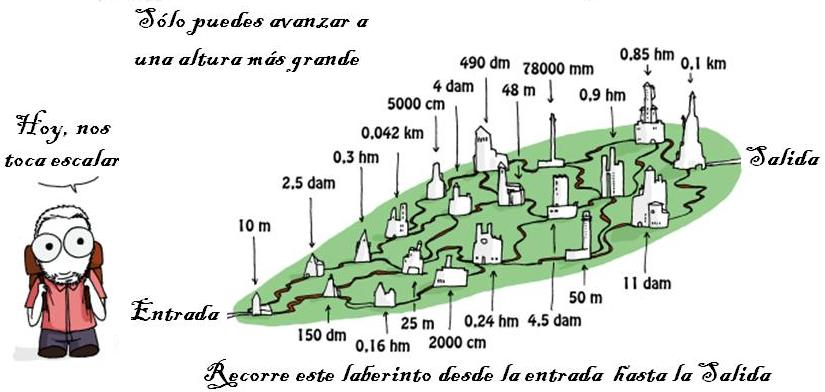
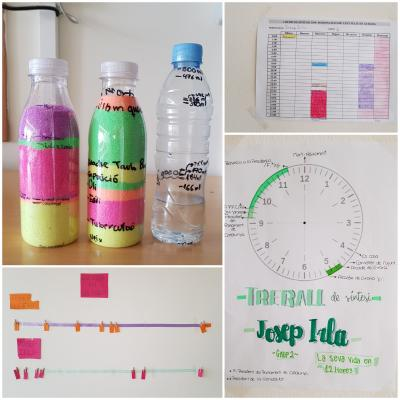
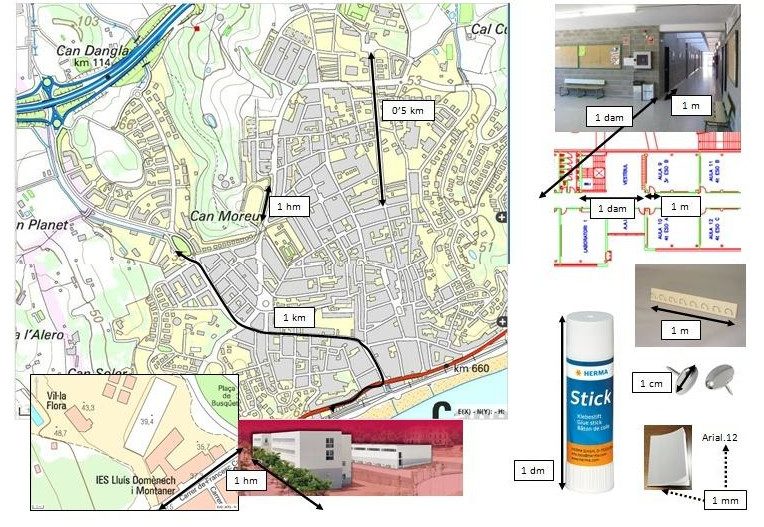
Aquest primer bloc de sabers recull la necessitat que l’alumnat desenvolupi el sentit de la mesura a partir del reconeixement d’atributs mesurables en objectes i l’adquisició de patrons que li serviran de base per poder establir quantitats, fer comparacions i estimacions. Cal que aquests patrons s’acabin integrant de forma natural en el seu coneixement com a unitats de referència, no només sabent-ne l’existència, sinó tenint una representació mental i física del que mesuren. És per això que recomanem un aprenentatge basat en activitats experimentals i on es fomenti la conversa matemàtica. Malgrat que sembli una evidència, només es pot desenvolupar el sentit de la mesura mesurant.

Tal com s’ha comentat en les consideracions generals, els alumnes ja tenen experiències sobre mesuraments a la primària, i han treballat amb unitats angulars, de longitud, àrea, capacitat, massa, temps, etc. Cal recollir aquest treball i els aprenentatges assolits per tal de donar-los una continuïtat, aprofundir amb noves situacions, reconèixer relacions d’equivalència i saber operar amb les quantitats obtingudes.

Cal cuidar la introducció i el treball amb unitats poc convencionals i aquelles que impliquin mesures derivades com és el cas del metre quadrat, el metre cúbic i els seus múltiples i submúltiples. Malgrat que en alguns casos l’alumnat ja ha pogut tenir experiències a l’educació primària amb activitats que preveuen l’ús d’unitats, és recomanable insistir a oferir propostes d’experimentació on intervinguin magnituds i mesures de superfícies, volums de sòlids i líquids, així com la descoberta d’equivalències. Donada la importància que es dona a les propietats físiques dels cossos en els sabers de les ciències experimentals, aquests tipus d’activitats són una invitació a les connexions externes entre les matemàtiques i les mateixes ciències.

Comentaris sobre les connexions

En general, tot el sentit de la mesura a la secundària està estretament connectat amb el sentit espacial. Serà habitual proposar activitats on es tinguin en compte de manera interrelacionada sabers d’un sentit i de l’altre. Les magnituds podran pertànyer a objectes geomètrics i, si volem presentar situacions enriquidores i ben connectades, sovint la mesura i la geometria aniran plegades: unitats per mesurar el perímetre de la classe, l’àrea de la taula, la capacitat de la piscina municipal o de les llaunes de refresc…

A la vegada, en aquest bloc de sabers trobarem connexions amb el sentit numèric, concretament amb el bloc del sentit de les operacions #NUM.SO. Algunes unitats vindran derivades per les relacions entre altres magnituds i, per tant, caldrà tenir-les presents a l’hora d’establir-les i, com a conseqüència, fer operacions entre elles. Per exemple, 1 m² = 1 m x 1 m. Igualment ens passarà quan calgui operar amb quantitats d’una mateixa magnitud però mesurades amb diferents unitats. En aquestes situacions ens veurem obligats a establir unitats de mesura adients que permetin operar i convertir totes les mesures a quantitats expressades en la mesura establerta. A més a més, ens podem trobar amb quantitats expressades en notació científica, i per tant, amb potències de base 10, nombres decimals o fraccions.

També trobarem connexions amb el sentit estocàstic quan es proposin situacions que impliquin la mesura de la certesa o incertesa d’esdeveniments. En concret, amb el conjunt de sabers de predictibilitat i incertesa #EST.PI. En aquests casos no sorgirà una unitat de mesura però sí un grau qualitatiu que permetrà comunicar si un succés és més o menys probable que es produeixi.

Observacions sobre alguns sabers d’aquest bloc

Aquest bloc de sabers recull la importància que l’alumnat sigui capaç de reconèixer magnituds en objectes del seu entorn, i establir conjuntament unitats de referència per tal de poder fer mesuraments i estimacions. És important acompanyar l’alumnat perquè copsi la necessitat d’aquest consens que li facilitarà no tan sols resoldre situacions de mesura sinó també la comunicació, i fer que la quantitat mesurada sigui entesa de la mateixa manera per tothom.

La identificació d’atributs mesurables, així com l’elecció d’unitats patró, permetran explorar la mesura d’elements, especialment els geomètrics. No obstant, seguint amb el treball dut a terme a primària, serà convenient parlar del temps cronològic, la temperatura, la capacitat, etc.

En funció de la mida o la quantitat, apareix de forma natural la necessitat d’emprar altres unitats de mesura d’un mateix atribut. En moltes situacions, caldrà que l’alumnat mostri destresa en l’ús de factors de conversió per fer canvis d’unitats i les operacions que li siguin necessàries; però això està més relacionat amb el bloc de sabers de mesurament.

És important fer emergir una consciència col·lectiva de la conveniència de disposar d’un sistema mètric comú. El coneixement de la història, les necessitats sorgides i els diferents escenaris que han esdevingut on la mesura n’ha estat protagonista, dotaran de context alguns problemes, facilitaran que se’n comprengui la resolució i ensenyaran a l’alumnat models aplicables a noves situacions.

Finalment, amb el sentit estocàstic, apareix l’estudi de la mesura de la incertesa. Una mesura que no està associada a un atribut amb una unitat específica, sinó al grau de certesa o incertesa amb què es produeix un esdeveniment.

Comentaris sobre els sabers essencials i d’ampliació

Es destaquen com a essencials els sabers que tenen una clara connexió amb altres sentits, a part de l’espacial. D’aquesta manera es vol posar èmfasi en l’elaboració de propostes que permetin un aprenentatge significatiu i ben connectat. Així doncs, creiem que per assegurar el saber #1.MES.MA.G caldrà que l’alumnat hagi assolit altres sabers que depenen del mateix bloc. L’establiment d’unitats per poder operar entre elles i establir-ne de noves comporta que ja s’hagin treballat prèviament situacions on la resta de sabers anteriors de magnitud hagin estat presents. En cap cas s’ha volgut significar aquest saber com a bàsic. Tots els sabers proposats són considerats importants i necessaris de ser treballats, però la tria d’aquest com a essencial ve donada pel seu caràcter aglutinador; per la necessitat d’haver incorporat els altres a l’hora de treballar el saber #1.MES.MA.G.

La determinació del grau qualitatiu de certesa o incertesa associat a esdeveniments tal com l’hem recollit en el saber #1.MES.MA.H apareix al llarg de l’educació primària. El fet d’escollir-lo com a essencial té la voluntat d’assegurar que tot l’alumnat, en finalitzar aquest curs, hagi pogut treballar activitats sobre mesura de la probabilitat que els permeti aconseguir aquest saber i, alhora, desenvolupar els sentits estocàstic i de la mesura conjuntament.

Recursos i activitats

Recursos i activitats generals per al bloc de sabers

En aquest apartat volem destacar l’article que van escriure David Barba i Cecilia Calvo per a la revista SUMA de la FESPM, en el número 77. Rep el títol d’Algunas actividades para hablar de medida (Barba & Calvo, 2014). És un bon article que, malgrat estar enfocat a la primària, presenta tot un seguit d’activitats ben estructurades per treballar aquest sentit, com ara el significat de mesurar, l’ús d’unitats, d’instruments i la necessitat de fer bones estimacions.

Recursos i activitats per treballar sabers concrets

A continuació, es presenten algunes idees sobre recursos i activitats d’aprenentatge que poden contribuir a l’adquisició dels sabers d’aquest bloc.

A. Identificació d’atributs mesurables en objectes matemàtics o físics, en el nostre entorn.

Per treballar el saber #1.MES.MA.A es pot demanar a l’alumnat que porti objectes quotidians on identifiqui atributs mesurables, sense especificar primerament a quins ens estem referint. No es tracta de portar instruments de mesura, sinó objectes on s’expliciti o es pugui mesurar una magnitud. Ens podem trobar llaunes, paquets o bosses d’aliments, gots, gerres… D’aquesta manera, mitjançant una posada en comú i en grups de 3 o 4, s’observarà si tenen adquirit el concepte de magnitud i quines són les que reconeixen fàcilment. Aleshores, proposarem fer un llistat per cada grup, anotant el nom dels objectes o incorporant-ne una fotografia, i tot seguit indicar quina o quines magnituds hi identifiquen. L’activitat prosseguirà detectant magnituds en elements que estiguin a la mateixa classe (la taula, el passadís, la pissarra, els penjadors…). Sempre que tenim una situació matemàtica a l’aula no hem de perdre l’oportunitat de fer-nos preguntes. És important, però, saber gestionar l’activitat i això implica decidir quines preguntes fem i quan les fem. En aquesta línia pot ser interessant proposar alguna situació en què l’alumnat es pugui arribar a preguntar si certes qualitats són magnitud o no, com el color, la bellesa o el gust. Ensenyar a l’alumnat a fer-se bones preguntes ha d’estar implícit en qualsevol proposta d’aula, ja que aquestes seran motor de futures indagacions i, com a conseqüència, d’aprenentatge.

B. Establiment d’unitats patró de mesura (a partir del propi cos, unitats antropomètriques o d’objectes coneguts propers a l’alumnat) adequades a cada situació.

El professor Alberto Herrero ens ofereix una proposta amb el nom La necessitat de les unitats de mesura, adaptada dels dossiers de matemàtiques de l’INS El Sui, on es dona rellevància al saber #1.MES.MA.B. En un primer moment trobem l’activitat «El joc dels nusos», en què es parteix de dues cordes idèntiques. Una se li dona a un alumne i se’l convida a sortir de classe, o donar l’esquena a la resta del grup, de manera que no pugui veure com li fem tres nusos a l’altra corda. Aleshores un altre company, d’esquena al primer però veient la corda amb els tres nusos, li ha d’explicar on estan situats sense utilitzar cap unitat de mesura del sistema mètric decimal (SMD), amb l’objectiu que el que escolta els faci en la mateixa posició que en l’altra corda. En lloc de nusos podem emprar agulles d’estendre roba. Mentrestant, caldrà anotar les paraules importants que s’utilitzin a l’hora de donar les instruccions, i reflexionar sobre els problemes apareguts per transmetre on estaven situats els nusos. Per tal de ser precisos amb el resultat, sorgirà la necessitat d’establir una unitat de mesura que faciliti la comunicació entre els dos alumnes. La competència específica sobre comunicació, C7, serà fonamental al llarg de tot l’exercici. La proposta continua amb dues activitats on es comenten algunes unitats de mesures emprades al llarg de la història per a diferents magnituds, i es convida l’alumnat a inventar-se unitats per mesurar objectes de mides diferents de la mateixa classe. D’aquesta manera, a partir de contextos històrics, es desenvoluparà la proposta fent significativa les connexions externes existents entre la matemàtica i la societat.

C. Comparació de les diferents unitats de mesura per a un mateix atribut.

La necessitat de les unitats de mesura

És habitual trobar activitats centrades en l’assoliment del saber #1.MES.MA.C. Amb tot, és important que aquestes estiguin contextualitzades i surtin d’una necessitat a l’hora de fer mesures. Trobarem molts exercicis que conviden a comparar unitats i fer canvis d’una a l’altra. Justament en propostes com La necessitat de les unitats de mesura, vista per al saber #1.MES.MA.B, on l’alumnat s’inventa unitats per mesurar, és on podem aprofitar per fer aquest tractament de la conversió entre unitats. El mateix professor Alberto Herrero estira la seva activitat amb Idea de les unitats de mesura demanant als alumnes que associïn un objecte quotidià o una situació a diferents unitats de mesura. D’aquesta manera s’aconsegueix que l’estudiant tingui una imatge mental de cadascuna de les unitats i se li facilita la possibilitat de comparar-les. En aquest full es poden veure les tries que va fer l’alumnat de dues classes.

Marro de nou i Cadena de las unidades

El professor Lluís Mora, a través del seu blog Marro de nou, ens exposa els beneficis del joc com a eina d’aprenentatge, i la necessitat d’oferir un ventall ampli de tipologia d’activitats a les nostres aules: cal diversificar les propostes! Ho trobarem a l’entrada Parlem una estona de #jocs: «Un juego». Implicacions per a l’aula. Amb aquesta mateixa idea, Ana García Azcárate, del Grupo Azarquiel, té una pàgina web, Jocs i Matemàtiques, plena de recursos i activitats on podem trobar el joc «Qui té?... Jo tinc» aplicat a Cadena de las unidades. Les instruccions són força senzilles i es pot adaptar perfectament a moltes situacions. En aquest cas les preguntes que surten tenen a veure amb conversions entre unitats de mesura de diferents magnituds. En el mateix portal tenim Los laberintos de las unidades de medida, en què es comparen mesures fetes amb múltiples i submúltiples d’una mateixa unitat. L’alumnat es trobarà amb una activitat interactiva en la qual haurà de completar diverses taules amb unitats de longitud, capacitat i massa. Aquesta activitat permetrà entendre les relacions i comparacions entre les diferents unitats de mesura, i es presentarà com un «laberint» que han de resoldre mitjançant les seves habilitats de conversió. L’objectiu és que l’alumnat practiqui les conversions i discuteixi amb els companys sobre les seves estratègies per trobar els resultats correctes. Es fomentarà el treball en grup per incentivar la comunicació i el raonament compartit.

Ana García Azcárate. *Los laberintos de las unidades de medida*

Per tal d’establir conversions entre unitats d’una mateixa magnitud recomanem emprar les taules de proporcionalitat. D’aquesta manera ajudarem l’alumnat a donar significat a les operacions que fa. De vegades s’ha utilitzat la regla de tres per a aquestes situacions, entesa com un procés mecànic que facilita la conversió, però allunyat completament del raonament i la comprensió sobre el que s’està fent. És per aquesta raó que les taules de proporcionalitat són una eina millor que facilita aquests processos.

km	m	cm	m
1	1.000	100	1
42	42.000	1000	10
0,42	420	5000	50

En les dues taules de proporcionalitat anteriors veiem com podem arribar a deduir quants metres representen 0,42 km partint de la relació que 1 km equival a 1.000 m. Aleshores, multiplicant per 42 tenim que 42 km equivalen a 42.000 m, i finalment per arribar a 0,42 km dividim per 100, per tant, 0,42 km corresponen a 420 m. Un procés similar ens conduiria a deduir quants metres són 5.000 cm. Començant per la relació que 100 cm són 1 m, multiplicant per 10 tenim que 1.000 cm són 10 m. Així doncs, només ens queda multiplicar per 5 per arribar a la conclusió que 5.000 cm són 50 m.

En aquests tipus d’activitats, l’alumnat veurà la necessitat d’establir la unitat de mesura que permetrà fer comparacions i convertir totes les altres a la unitat escollida. Si marquem només la relació d’equivalència i l’objectiu (quantitat que cal passar d’unitat), permetrem que cada alumne pugui deduir el seu camí per tal d’arribar-hi i, per tant, posar en valor el raonament.

km	m	cm	m
1	1.000	100	1

0,42		5000

En el cas de 0,42 km podem trobar raonaments que portin primer a buscar la quantitat de metres que representen una centèsima de quilòmetre, per a, després, obtenir els metres de quaranta-dues centèsimes de quilòmetres. Altres, potser no arribaran a calcular-ho exactament però sabran trobar-ne una estimació deduint que 0,42 és poc menys que 0,5 i que, per tant, serà una quantitat aproximada i inferior als 500 m, etc. Recordem que l’objectiu de l’activitat és d’ordenació i, per tant, qualsevol argumentació que permeti concloure quina és més gran o més petita entre dues mesures donades, serà vàlida i, alhora, consolidarà la relació entre unitats.

Marca-rutes, Trencaclosques de mesures, Matgrams i Dòminos.

En el número 67 de la revista SUMA de la Federación Española de Sociedades de Profesores de Matemáticas (FESPM), trobem un article interessant amb el títol ¡Medidas, las justas! (Hans Martín et al., 2011), escrit pel Grupo Alquerque de Sevilla, i on s’expliquen quatre jocs/passatemps per treballar la conversió entre unitats de mesures: Marca-rutes, Trencaclosques de mesures, Matgrams i Dòminos. Recomanem anar variant l’agrupació a classe, fent que alguns d’aquests reptes puguin ser resolts per parelles o grups de tres, per potenciar la comunicació matemàtica i l’aprenentatge entre iguals. Cal deixar algunes activitats per a la resolució individual, ja que també és important educar el nostre alumnat a enfrontar-se a reptes per si sols.

En la mateixa pàgina web d’Ana García Azcárate, esmentada anteriorment dins d’aquest saber, també trobarem diferents dòminos, com el de longituds, i el de capacitats i volums del grup Alquerque. Presentar a l’aula recursos diferents ajudarà a atendre les diverses formes d’aprenentatge de l’alumnat.

NRICH: Place your orders

Un recurs molt interessant per treballar el raonament i prova dins d’aquest saber és la proposta que ens fa el portal NRICH amb Place your orders. Es dona un conjunt de quatre quantitats que caldrà ordenar de petit a gran. Per decidir-ho, l’alumnat potser haurà de buscar informació addicional o fer alguns experiments. Caldrà argumentar la classificació final. Per veure un exemple d’aquests conjunts de quatre quantitats tenim el següent:

El temps

de vida d'un hàmster.
perquè la llum ens arribi des de l'estrella més propera que no sigui el sol.
entre dues copes del món de futbol.
perquè tots els glòbuls vermells del teu cos siguin substituïts 10 vegades.

La vida en 1 h, 12 h, una setmana, un any, un metre, un litre, 360°...

Amb l’activitat La vida en 1 h, 12 h, una setmana, un any, un metre, un litre, 360°... de Paula López, Dani Sans i Xavi Simon, es treballen els canvis d’unitats i la proporcionalitat numèrica mitjançant representacions molt creatives de la biografia d’algun personatge famós ja mort. Pot aprofitar-se la setmana de la ciència, per exemple, per parlar de dones científiques i representar cadascuna de les seves vides com si hagués passat en una hora, un dia, una setmana, un mes, un any, un metre, un quilogram, un litre...

En l’enllaç a l’activitat trobarem la descripció de la proposta, així com alguns aspectes didàctics i metodològics importants per dur-la a terme.

D. Adquisició, per consens, d’una unitat de mesura de referència comuna.

Sense unitats no mesurem

La proposta Sense unitats no mesurem de la professora Maria Rosa Latorre, i que trobarem a l’ARC, té com a principal objectiu que l’alumnat vegi la necessitat d’establir una unitat patró a l’hora de mesurar qualsevol magnitud; concretament, el saber #1.MES.MA.D. Es parteix de les unitats antropomètriques per mesurar longituds i d’unitats quotidianes per mesurar capacitats, i es prenen diferents mesures de manera que sorgeix la necessitat d’establir una unitat patró.

Referents de les unitats de longitud

Seguint amb el treball del professor Alberto Herrero esmentat en sabers anteriors, és una bona opció establir per consens les unitats de mesura i construir un gran mural amb fotografies i dibuixos que els recordi l’equivalència. Un exemple fet per aquest docent i els seus alumnes de l’IES Lluís Domènech i Montaner de Canet de Mar és Referents de les unitats de longitud.

De la mateixa manera construïm referents d’unitats de superfícies i d’unitats de volum i capacitat.

Alberto Herrero. *Referents de les unitats d’àrea o superfície*

Alberto Herrero. *Referents unitats de volum i capacitat*

Fotografia matemàtica

Una bona activitat també és la fotografia matemàtica. Podem demanar a l’alumnat que fotografiïn un concepte o una idea matemàtica, en el nostre cas, una unitat de mesura. D’aquesta manera podem treballar la representació de conceptes i relacions matemàtiques lligades amb la magnitud. També podem optar per mostrar una fotografia i demanar a l’alumnat quin títol li posarien, entenent que aquest farà referència a les matemàtiques que ha volgut mostrar el seu autor. En fotografia matemàtica és tan important mostrar una idea matemàtica com l’assignació d’un bon títol. La primera acció ajuda l’alumnat a la seva representació i a connectar les matemàtiques amb el seu entorn proper. En la segona es posarà de manifest l’habilitat comunicativa de l’autor o autora per fer notòria la matemàtica que hi ha observat. Són un bon recurs per fer-se preguntes i alhora generadors de problemes. Tot seguit en veiem un exemple en la fotografia Unitat de macromesura de la professora Marta Arbolí, premi accèssit 2010 del concurs de fotografia d’ABEAM. Només veient la imatge, quin títol li haguéssiu posat?

E. Avaluació de la importància de l’establiment del sistema mètric decimal (naixement del metre).

Quèquicom de 3Cat, El sistema mètric

Per treballar el saber #1.MES.MA.E, tenim el capítol del programa Quèquicom de 3Cat, El sistema mètric, en el qual ens presenten una passejada des de la mesura de la Terra feta per Eratòstenes fins a l’establiment de l’actual sistema mètric. Durant aquest vídeo, podrem valorar la importància que va tenir Catalunya en tot aquest procés. Un cop feta la visualització, podem localitzar els diferents vèrtexs geodèsics que es van fer servir per establir el metre, i com a ampliació per què no fem una excursió a algun d’aquests punts?

La figura de Pierre Méchain

La pàgina La mesura del planeta es va fer a Barcelona de Betevé està centrada en la figura de Pierre Méchain i el seu pas per la ciutat comtal per tal de mesurar l’arc de meridià de Dunkerque a Barcelona. És un bon recurs per mostrar els punts emblemàtics de la capital catalana relacionats amb aquest fet memorable i alhora una oportunitat més per apropar les matemàtiques a partir de la història i la societat.

InfoK: El sistema mètric

El programa InfoK de 3Cat també va dedicar un vídeo curt a explicar els orígens del sistema mètric, dins de la secció Piriskopi. El vídeo de menys de tres minuts es diu El sistema mètric. Encara que les explicacions són molt adients per a l’alumnat de 1r d’ESO, el treball previ dels sabers anteriors de magnitud permetran que l’alumnat entengui perfectament la necessitat d’establir un sistema de mesures internacional.

"Una passejada per l'origen del Sistema Mètric Decimal i del Sistema Internacional d'Unitats" Anton Aubanell

El professor Anton Aubanell té una conferència amb el nom Una passejada per l’origen del sistema mètric decimal i del sistema internacional d’unitats. Per visualitzar-la, primer caldrà donar-se d’alta gratuïtament al portal Vimeo. Les explicacions d’Aubanell enriquiran, de ben segur, les propostes docents i el coneixement dels mateixos alumnes, aprofitant les connexions històriques que conté aquest saber #1.MES.MA.E.

Anton Aubanell. *Una passejada per l'origen del Sistema Mètric Decimal i del Sistema Internacional d'Unitats*

Llibres

Hi ha molts llibres que tracten el tema del naixement del metre:

La mesura del món (Guedj, 1998)
La medida de todas las cosas (Alder, 2003)
La medida de todas las cosas: Un viaje por los diferentes sistemas de medición (Whitelaw, 2010)…,
però recomanem especialment, per als docents, El naixement del metre (Moreu-Rey, 1986).

SMD i les imperials

Avui en dia encara convivim amb mesures pròpies del SMD i les imperials: peus, polzades, milles, iardes, lliures, unces, galions, o la mateixa temperatura, expressada en graus Celsius o Fahrenheit.

Es pot demanar una cerca de productes anglosaxons per mirar l’etiquetatge i comparar-lo amb el d’aquí. Per exemple les llaunes de refresc, els paquets d’arròs, etc.

En les imatges següents veiem unitats que no són habituals en el nostre país. Són una invitació perfecta per identificar-les, saber a quina magnitud fan referència i trobar quina seria la seva equivalència si les expressem en una unitat més comuna en el nostre entorn.

La tecnologia no es troba exempta d’errades

Per tal de copsar la importància del sistema de mesures, i que la història de la ciència i la tecnologia no es troba exempta d’errades, es pot parlar de l’accident de la Mars Climate Orbiter, l’any 1999, per part de la NASA, a causa d’un problema de canvi d’unitats. Aquí tenim un vídeo fet en col·laboració amb la Cátedra de Cultura Científica de la UPV/EHU, i emès en el programa de ciència Órbita Laika de RTVE.

Cátedra de Cultura Científica de la UPV/EHU. *El accidente de la Mars Climate Orbiter*

A partir del vídeo és important reflexionar sobre diferents aspectes amb l’alumnat, que tindran la seva importància en la resolució de problemes i la gestió que facin de les seves pròpies errades:

Una quantitat de mesura, si no va acompanyada de la unitat amb la qual ha estat mesurada, no té un significat complet.
Per poder comparar i operar amb quantitats de mesura cal que estiguin mesurades en la mateixa unitat.
Els problemes no s’acaben quan s’obté un resultat. Cal analitzar-los, i en cas de no obtenir els resultats esperats, buscar les raons que l’han produït per tal que les errades siguin els inicis de nous aprenentatges.

F. Adequació de la unitat de mesura als atributs dels objectes.

Encara que de forma implícita hagi pogut sortir en diferents propostes anteriors, adequar la unitat de mesura a les magnituds d’un objecte, saber #1.MES.MA.F, facilitarà no només fer els corresponents mesuraments, sinó també poder expressar les quantitats obtingudes de manera que s’entenguin perfectament els valors.

Explorant els ordres de magnitud

Mostrar el món micro i el macro permetrà entendre perfectament aquest saber. Una manera és a partir del vídeo Potències de 10 que trobarem en el portal Dígits: del número al bit. Partint de la distància d’un metre, una mesura fàcilment identificable per a l’ésser humà, una càmera es va allunyant de l’objectiu inicial i mostra què es visualitza a mesura que s’incrementa la distància fins a arribar als anys llum, i també a l’inrevés, apropant-se cada cop més fins a distàncies d’un femtòmetre. Un recurs similar el tenim al portal HTWINS amb l’Escala de l’Univers.

Un cop vist el vídeo pot ser interessant fer la proposta per al bloc de mesura Explorant els ordres de magnitud que Anton Aubanell descriu en les seves Orientacions per a la millora de la geometria a l’ESO (Aubanell, 2015).

Aquesta proposta conté algunes activitats que no serien adequades per al curs que estem tractant, però la construcció de frisos per a longituds, massa i temps, com el de la imatge anterior, són un bon treball de representació perquè l’alumnat sàpiga adequar la unitat de mesura a l’atribut de l’objecte que cal mesurar. L’ús dels passadissos del centre permetrien fer una excel·lent exposició sobre ordres de magnitud treballant-ho conjuntament amb les àrees de ciències i tecnologia. Per tal de dur a terme l’activitat cal tenir en compte que el concepte «ordre de magnitud» va lligat a la notació científica, a les propietats de les potències i, depèn de com, al treball d’aquestes amb exponents negatius. És important adaptar-la en funció del coneixement que tingui l’alumnat sobre aquests sabers corresponents al sentit numèric, o proposar-la sabent que esdevindrà una oportunitat per introduir i treballar els sabers esmentats.

Aquest treball també es pot fer a partir de la gran proposta del professor Jordi Domènech Casal amb Solar System Pathway. Segons el mateix autor, es tracta d’una activitat d’aprenentatge de l’astronomia en primera persona seguint metodologies actives properes a l’ABP. Es proposa a l’alumnat elaborar una maqueta urbana del sistema solar de 10 km de llargada, en la qual ubicaran els diferents cossos celestes, cadascun al lloc que pertocaria i indicant la mida que tindria, amb l’objectiu de percebre les proporcions reals dels elements del Sistema Solar i crear un itinerari cultural al municipi. La realització d’aquesta activitat enforteix les connexions externes entre les matemàtiques i altres àrees de coneixement. En particular, es treballa el saber de Biologia i Geologia referent a l’elaboració de maquetes i models per a la representació i comprensió de conceptes, processos o elements de la natura, i els sabers de Ciències Socials: Geografia i Història sobre ubicació espacial.

Thousands and millions de NRICH.

Podries córrer mil metres en un minut? Els éssers humans viuen fins a un milió d’hores? Aquestes són dues mostres d’exemple dels diferents reptes que es plantegen en l’activitat Thousands and millions de NRICH. Amb aquestes qüestions podem centrar la classe en la resolució de problemes. L’alumnat es veurà obligat a treballar amb nombres grans, però alhora caldrà que faci canvis d’unitats per tal de resoldre’ls. La vida humana l’acostumem a expressar en anys i no pas en hores. Així doncs, caldrà adequar les unitats per poder realitzar les primeres investigacions i fer-ne els càlculs. Es recomana que per a totes les preguntes es faci una estimació, posant-la inicialment en el full de treball. Finalment, després de fer els càlculs i obtenir els resultats, serà interessant avaluar la diferència obtinguda entre l’estimació i el valor resultant. Des d’un punt de vista organitzatiu, pot ser enriquidor proposar-ho en parelles per fomentar la conversa matemàtica, compartir estratègies de resolució i valorar els resultats obtinguts.

G. Elecció d’unitats de mesura adients per poder operar entre elles i, si escau, per generar-ne de derivades (per exemple, 1 m × 1 m = 1 m2). [ESS] #NUM.SO

El saber #1.MES.MA.G es treballa de forma natural en la resolució de problemes en què les dades provinguin de magnituds. Hi trobem dos aspectes rellevants:

D’una banda, la necessitat de triar la unitat de mesura per fer tots els mesuraments d’una determinada magnitud, i com a conseqüència poder operar amb les mesures obtingudes. En aquest sentit serà necessari i imprescindible el canvi d’unitats, i ens apareixeran mesures amb nombres decimals o en notació científica. Per tal que aquest aspecte sigui significatiu es recomana posar-lo en un context d’experimentació i de resolució de problemes, com per exemple La recepta de Maria Rosa Latorre, on a partir dels ingredients de diferents receptes es treballen els canvis d’unitats i s’operen les quantitats.
L’altre aspecte que sorgeix en el mateix saber és la construcció de noves unitats de mesura derivades d’altres, com per exemple la unitat de superfície m², resultat del producte de dues magnituds expressades en metres, o el m³ a partir del producte de tres magnituds expressades en metres. Pot ser interessant construir entre tota la classe el metre quadrat a partir de quadrats de 10 cm de costat. Si volem construir-lo, quants quadrats de 10 cm de costat haurà de fer cada alumne?

Alberto Herrero

Aquesta construcció, com la del metre cúbic, permet a l’alumnat tenir una experiència que el connecta directament amb la mida real i alhora provoca fer equivalències entre les unitats representades:
- Quants centímetres quadrats mesura l’àrea de cada quadrat petit?
- Quants quadrats petits de 10 cm de costat hem necessitat per construir el quadrat gran?
- Quants centímetres quadrats té d’àrea el quadrat gran?
- Quants centímetres mesura el costat del quadrat gran?
- …
Totes aquestes preguntes permetran entendre la raó per la qual hem obtingut un quadrat d’1 m de costat, i per tant d’1 m² d’àrea. I alhora, les relacions d’equivalència
1 m² = 1 m x 1 m = 100 x 100 cm² = 100 cm x 100 cm.

H. Determinació del grau qualitatiu de certesa o incertesa associat a esdeveniments: segur, molt probable, poc probable, possible, impossible… [ESS] #EST.PI

El professor Sergio Gracia ens ofereix un Memory improbable que s’adequa perfectament al saber #1.MES.MA.H. L’activitat consta de tres moments i té com a primer objectiu treballar diferents graus de certesa o incertesa com «poc probable», «impossible», «segur»…, en aspectes de la vida quotidiana. Més endavant entra en la possibilitat de quantificar i acaba amb un Memory. És recomanable que, a més a més, es pugui construir un Probabilòmetre, una activitat dissenyada pel professor Francesc Massich.

Cal recordar que els sabers #1.MES.MA.G i #1.MES.MA.H són essencials, però que els recursos que s’acaben de descriure són només una proposta.

Llicenciat sota la Llicència Creative Commons Reconeixement CompartirIgual 4.0