L’últim es queda dempeus

A l’NRICH podem trobar l’activitat L’últim es queda dempeus, que consisteix que el conjunt de l’alumnat de classe, que està dempeus, tiri una moneda a l’aire i, si surt cara, es queda dempeus i, si surt creu, s’asseu. A l’activitat proposada se suposa que, inicialment, hi ha 250 alumnes que van tirant la moneda fins que l’últim alumne es queda dempeus.

Les preguntes inicials són:

• Creus que algú traurà 6 cares seguides?
• Quantes cares seguides espereu que hagi tret l’últim alumne que queda dempeus?
• Pots explicar el teu raonament?

A la mateixa activitat podem trobar una animació per fer simulacions amb 16 persones. Després d’experimentar es pregunta: Quantes persones caldria ser inicialment perquè hi hagués encara algú dempeus després de 10 tirades? Finalment, es fan preguntes sobre situacions similars com el jackpot, naixements i tirades d’una moneda.

Joc del 6

Una activitat molt semblant la proposa el Grup Cúbic a la jornada Un homenatge a Lluís A. Santaló des d’una perspectiva didàctica anomenada Joc del 6 que és similar a l’anterior, però fent servir un dau de 6 cares. En aquest cas un alumne tira el dau i s’asseu si li surt un 6.

Abans de dur a terme l’activitat experimentalment es demana a priori quin és el nombre de tirades que s’han de fer per tal que només en quedi un dempeus. Després es duu a terme l’activitat i es contrasta el resultat amb les conjectures fetes.

En la presentació podem trobar el raonament de com arribar a un model discret de la situació. Seria raonable pensar que en cada tirada la probabilitat de quedar-se dempeus és de \(\frac56\) i la de seure d’\(\frac16\). Per tant, en cada tirada anirà seient \(\frac16\) part de l’alumnat que queda dempeus.

Considerant que el procés d’eliminació és discret, podem modelitzar-lo, on \(N_0\) és el nombre d’alumnes de la classe i \(N(t)\) el nombre d’alumnes dempeus després de \(t\) tirades.

\(N(t) = N_0\cdot \frac56 \cdot \frac56 \cdots (t) \cdots\frac56 \cdot \frac56 = N_0\cdot (\frac56)^t\)

Suposem ara que hi ha 30 alumnes a classe, quina és la previsió d’alumnes que quedarà dempeus després de 10 tirades?

\(N(10) = 30 \cdot (\frac56)^{10} \simeq 4,85\)

Per tant, la previsió del model en diu que quedarien dempeus entre 4 i 5 alumnes.

Donat que a 4t d’ESO ja es treballa la funció logarítmica, podem saber quin és el nombre de tirades que necessitaríem perquè quedi només una persona dempeus en funció de la població inicial, que serà:

\(N_0 \cdot (\frac56)^{t} =1\)

Aplicant les propietats dels logaritmes:

\(\log_{\frac56}(N_0 \cdot (\frac56)^{t}) =\log_{\frac56}1\)

\(\log_{\frac56}(N_0) + \log_{\frac56}(\frac56)^{t} =\log_{\frac56}1\)

\(\log_{\frac56}(N_0) + t =0\)

\(t =-\log_{\frac56}(N_0) \)

\(t =\log_{\frac56}(N_0^{-1}) \)

\(t =\log_{\frac56}(\frac{1}{N_0}) \)

A tall d’exemple i suposant que a la classe hi hagi 30 alumnes, la previsió és que el nombre de tirades que hem de fer fins que només quedi 1 alumne dempeus és de:

\(t =\log_{\frac56}(\frac{1}{30}) = 18,65 \)

Per tant, la previsió és que necessitaríem entre 18 i 19 tirades perquè quedi només un alumne dempeus.

A la documentació podeu trobar l’enllaç a una construcció amb GeoGebra en què es representa el model discret i el model continu i la previsió de tirades dels dos models fins que queda una única persona dempeus:

En la presentació i la construcció de GeoGebra també es pot visualitzar el gràfic si es considera que el procés d’eliminació és continu, més adequat per a batxillerat en el moment que es treballa la funció derivada.

Com podem observar, amb el model discret i amb el model continu s’obtenen resultats molt semblants.

Una situació real anàloga seria el model matemàtic de desintegració radioactiva que segueix també el model exponencial.

Fitxes de colors per combinatòria.

Una activitat inicial per començar a treballar la combinatòria és la que proposa Anton Aubanell a l’ARC titulada Fitxes de colors per combinatòria.

Els objectius de l’activitat són plantejar el problema general de la combinatòria, raonar sobre els criteris de formació d’agrupacions i donar suport a la deducció de fórmules de recompte.

Agafant com a punt de sortida l’ordenació de les bases nitrogenades (l’adenina (A), la timina (T), la guanina (G) i la citosina C) a les molècules d’ADN, es fa la pregunta: Quantes seqüències diferents de tan sols deu bases podem formar amb les quatre bases nitrogenades que indicarem per a A, T, G i C?

Per començar a treballar es dona a cada subgrup d’alumnes una col·lecció prou gran de fitxes de 4 colors diferents i se’ls demana que formin tot els grups que puguin amb tres fitxes i que indiquin quants de grups han trobat.

L’activitat està proposada d’aquesta manera per tal que de forma natural apareguin dues preguntes clau per treballar la combinatòria: Podem repetir color? Importa l’ordre?

El professorat no ha de respondre a aquestes preguntes i ha de deixar que cada grup prengui les seves decisions, de manera que el resultat anirà variant en funció d’aquestes decisions.

Així, els subgrups que hagin decidit que sí que importa l’ordre i sí que poden repetir colors tindran 64 grups de fitxes diferents.

Als subgrups que hagin decidit que no importa l’ordre i que no poden repetir colors els sortiran només 4 grups diferents.

Als subgrups que hagin decidit que sí que importa l’ordre, però que no poden repetir color els sortiran 24 grups diferents.

I finalment als subgrups que hagin decidit que no importa l’ordre, però sí que poden repetir color els sortiran 20 grups diferents.

Després que cadascú doni la seva resposta, es fa una posada en comú i es mira quins elements diferents s’obtenen en funció de les decisions preses: si importa o no l’ordre de les fitxes i si es poden repetir colors o no.

A continuació, es proposen més preguntes indicant en cada cas quines són les condicions i apareixen les Variacions ordinàries, les Variacions amb repetició, les Permutacions, les Permutacions amb repetició, les Combinacions i les Combinacions amb repetició.

La darrera pregunta de l’activitat ens porta a recuperar la pregunta inicial: Quantes seqüències diferents de tan sols deu bases podem formar amb les quatre bases nitrogenades que indicarem per a A, T, G i C?

A l’ARC es pot trobar un guió complet de l’activitat.

Ostres, la clau!

A la sèrie Àlia hi podem trobar el capítol Ostres, la clau! en què l’Àlia, ara tècnica en informàtica, ha de trobar la clau per restablir el sistema informàtic d’una empresa en un temps molt limitat. La seva habilitat emprant amb lògica les poques informacions de què disposa, els seus coneixements de combinatòria i una mica de sort li permetran resoldre el problema i descobrir que darrere de la clau s’amaga un personatge molt especial…

En l’enllaç següent podeu trobar el document de Suport didàctic creat pel Creamat.

Quin cadenat és més segur?

A la XXVI jornada de didàctica d’ABEAM, Susana Vásquez, Berta Barquero i Marianna Bosch de la UB van presentar la situació d’aprenentatge Quin cadenat és més segur?

Tal com s’explica en la descripció del taller:

Viurem una situació d’aprenentatge al voltant de la seguretat dels cadenats i amb l’objectiu de treballar les estratègies de comptatge i els sabers de la combinatòria.

S’ofereix una mostra de 6 cadenats, amb un funcionament diferent i es planteja la pregunta: “Quin cadenat és més segur?”. La idea central és que, en comptes de proporcionar directament les fórmules i els conceptes de la combinatòria tradicional, es planteja una pregunta que motivi els alumnes a investigar i descobrir la combinatòria per si mateixos.

Aquesta pregunta es converteix en el punt de partida d’una investigació en què els alumnes manipulen alguns cadenats reals, n’analitzen les característiques i desenvolupen les seves pròpies estratègies per calcular el nombre de codis possibles.

A mesura que s’avança en la recerca, es van construint models, definint variables i establint relacions, la qual cosa permet comprendre la lògica darrere de la combinatòria i la seva aplicació en situacions reals.

En l’enllaç següent podeu trobar tota la informació, amb la presentació que es va dur a terme al Cesire i també les dades de contacte de les professores responsables per accedir als materials.

Simplex Lock

Lluís Mora va presentar una altra activitat també a la XXVI Jornada d’ABEAM anomenada Simplex Lock, extreta del web Making Mathematics, en què es desenvolupen projectes de recerca oberts amb alumnat de secundària. Per resoldre-la completament, es necessiten diferents sessions de classe en què cal anar guiant la feina de l’alumnat.

«Aquí veieu un cadenat fet per l’empresa Simplex. Anuncia "milers de combinacions". Estan dient la veritat?»

Una combinació és una seqüència de 0-5 pressions. Els impulsos han de seguir aquestes regles:

• Podeu prémer qualsevol nombre de botons, de 0 a 5.
• Una vegada que es prem un botó, es manté pitjat (per tant, no es pot tornar a utilitzar en una pressió posterior).

Algunes combinacions possibles:

• {1 2 3} {4 5} (prem 1, 2, 3 junts i després prem 4 i 5 junts)
• {4 5} {1 2 3} (l’ordre de les pressions compta, però l’ordre dins d’una pressió, no)
• {1}{3}{4, 5} (no cal que feu servir tots els botons)
• {1 2 3 4 5} (prem tots els botons alhora)
• {1} {3} {2} {5} {4} (utilitzant els cinc botons en cinc pressions)
• {} (sense combinació; la porta està oberta)

Finalment, es veu com, si també tenim en compte l’opció de no pitjar cap nombre i, per tant, deixar el pany obert, hi ha 1.082 opcions diferents, amb la qual cosa es pot posar en qüestió l’afirmació de l’empresa.

Al web podem trobar el plantejament del problema: què es treballa, quines són les activitats prèvies a l’abordament de la situació, consells per a la resolució, recursos per al professorat, estratègies per portar el problema a l’aula, possibles extensions i exemples del treball de l’alumnat.

Snooker

Una altra activitat interessant de l’NRICH és la titulada Snooker en què s’ha de calcular la probabilitat que un jugador A guanyi un torneig «al millor de 15 jocs» a un jugador B sabent quina és la probabilitat p que A guanyi B en una partida. En la proposta es plantegen diferents valors per a p. Així:

P(Guanyi A)=P(Guanyi A/8 partides)+P(Guanyi A/9 partides) +...+P(Guanyi A/15 partides)

El Mètode Montecarlo

Un dels mètodes que es fa servir és el Mètode Montecarlo, ideat inicialment per John von Neumann i Stanislaw Ulam al laboratori de Los Álamos, al projecte Manhattan. Podem trobar-ne una explicació detallada al capítol Ruletas y bombas atómicas: EL MÉTODO MONTECARLO de la sèrie Derivando d’Eduardo Sáenz de Cabezón.

Una primera activitat que es podria fer a classe utilitzant aquest mètode és trobar una aproximació de \(\pi\).

Dibuixem un quadrat de costat 2 unitats i hi inscrivim un cercle de radi 1 unitat. L’àrea del quadrat serà de 4 unitats quadrades i l’àrea del cercle serà de \(\pi\) unitats quadrades.

Ara tirarem grans d’arròs a l’atzar dintre del quadrat. Cal esperar que la proporció entre els grans d’arròs que caiguin dintre del cercle respecte dels que han caigut dintre del quadrat seguirà la proporció \(\frac{\pi}{4}\)

Per tant, \(\frac{\textrm{Grans al cercle}}{\textrm{Grans al quadrat}} \simeq \frac{\pi}{4}\) de la qual cosa podem extreure una primera aproximació de  \( \pi = 4 \cdot \frac{\textrm{Grans al cercle}}{\textrm{Grans al quadrat}} \) 

Evidentment, com més tirades fem, més bona serà l’aproximació que obtindrem.

Aquesta activitat seria fàcilment programable, donant d’exemple la proposta de Raül Fernández titulada Aproximació de pi per Montecarlo feta amb Snap.

Imaginem ara que volem calcular l’àrea d’una figura irregular: doncs podem fer el mateix procés per obtenir una aproximació d’aquesta àrea.

El Mètode de MonteCarlo es fa servir en molts camps com ara en microelectrònica, telecomunicacions, disseny per ordinador, control de qualitat, robòtica, meteorologia, arquitectura, etc.

Evidentment, l’ús de la programació per poder simular una quantitat molt gran d’experiments en poc temps ens permetrà arribar a resultats molt acurats.

Simulacions de l’atzar

A l’activitat Càlcul de probabilitats de Victòria Oliu hi ha un apartat titulat Simulacions de l’atzar en què es presenten 4 simulacions programades amb Scratch:

• Un dau perfecte
• Un dau trucat
• L’agulla de Buffon
• Les tres portes

Les tres vespes

Un altre exemple d’activitat que es pot resoldre per simulació és el que trobem a La Caixa de Varga titulat Les tres vespes.

El càlcul teòric de la mitjana com el valor esperat no està a l’abast de l’alumnat d’ESO i, per tant, podem trobar una bona aproximació fent una simulació. En l’enllaç següent podeu trobar una fitxa completa per dur a terme la simulació experimentalment.

En petits grups, l’alumnat pot fer diferents processos utilitzant un dau, per exemple 25, i fer una primera mitjana. Es poden contrastar els resultats obtinguts pels diferents grups per després acumular tots els valors i obtenir una mitjana de classe.

També es poden anar introduint els valors en un full de càlcul, representar la distribució obtinguda i obtenir la mitjana.

Es presenten els resultats obtinguts a una classe de 4t d’ESO el curs 23/24 a l’Institut El Joncar de Barcelona.

Font: elaboració pròpia.

La mitjana acumulada de les 200 tirades ens dona 9,72.

En la seva representació gràfica, podem veure que aquesta primera aproximació de la mitjana s’estabilitza al voltant del 10, que és el valor de la mitjana teòrica.

Una altra opció podria ser la de generar una programa amb el llenguatge de programació que s’hagi treballat al centre per fer moltes repeticions.

Mostrem el programa realitzat amb Phyton per l’alumne Adrià de Batlle per dur a terme la simulació:

Com podem veure, la simulació de 2.000 processos dona una mitjana de 10,23 molt propera a 10.

Com un complement a la feina feta per l’alumnat, al web també podem trobar simulacions fetes amb GeoGebra pel professor Jordi Font i amb Snap! pel professor Raül Fernández.

Problemes del Fem matemàtiques

Una lloc on trobar activitats molt interessants per tractar el saber #4.EST.PI.E és la llista dels problemes del Fem matemàtiques de les diferents edicions. Al seu web hi podeu trobar la informació detallada que s’estructura en tres fases, en què es resolen problemes en equip i individualment.

L’activitat del Fem matemàtiques, per a alumnat des de 5è de primària fins a 4t d’ESO, té per objectius:

• Potenciar el raonament matemàtic a través de la resolució de problemes.
• Fomentar la capacitat de comunicació i argumentació matemàtica presentant activitats per resoldre en equip i exigint l’elaboració d’informes detallats.
• Ajudar els nois a adquirir seguretat i confiança en les seves capacitats per fer matemàtiques presentant-los activitats motivadores i que els suposin un repte.
• Mostrar als professors activitats lligades a l’entorn i problemes adequats per treballar estratègies i desenvolupar actituds positives cap a aquesta disciplina.

A la pàgina Recull de problemes del Fem Matemàtiques podem trobar un recull dels problemes fets per totes les associacions de docents de matemàtiques de Catalunya per al FEM MATEMÀTIQUES des de l’any 1993.

Com a exemple, es proposa el problema Daus i triangles de la 1a fase per a 4t d’ESO del 2024, que ens permet treballar conjuntament el sentit espacial i el sentit estocàstic:

En Joan té molts bastonets de diferents mides, des d’1 cm fins a 6 cm (tots nombres enters). Juga a construir triangles a sorts. Per fer-ho, llança tres daus i agafa tres bastonets de la mida que indiquen els daus. Amb els tres bastonets intenta construir un triangle. Si ho aconsegueix, guanya el joc.

Tingueu en compte que, per poder construir un triangle, és necessari que la suma de dos costats qualssevol ha de ser estrictament superior al valor del tercer costat. Per exemple, amb 4, 5 i 6 podem construir un triangle que tingui els costats de 4 cm, 5 cm i 6 cm, però amb 1, 2 i 6 no es pot.

1. Quina probabilitat té de guanyar si en el primer dau li surt el número 4?
2. I si obté un 1 en el primer dau?
3. Imagineu que ara juga amb un dau tetraèdric (de quatre cares) amb els números 1, 2, 3 i 4. Si tira aquest dau 3 vegades, quina probabilitat té de guanyar?

Raoneu totes les vostres respostes.

A la primera fase, l’alumnat treballa al mateix centre en equips de 3 o 4 alumnes com a màxim. Cada grup ha d’elaborar un informe amb la resolució de cadascun dels 3 problemes en què es farà constar les dades del grup i les estratègies, experimentacions, reflexions, càlculs, verificacions… que s’hagin dut a terme durant el procés de resolució.

Com podem comprovar, es tracta d’activitats que requereixen el seu temps i en què el treball en equip és fonamental. En aquestes activitats, el professorat acompanya l’alumnat en el procés de resolució que, en gran part, es duu a terme fora de l’horari lectiu. Normalment, hi ha més de dos mesos de temps entre que es publiquen les activitats i es lliura l’informe final.

En aquesta activitat cal tenir en compte la desigualtat triangular per veure quan una combinació pot formar un triangle o no. Després ja cal trobar totes les combinacions de 3 nombres que generen un triangle i calcular-ne les probabilitats.

Representing Probabilities: Medical Testing

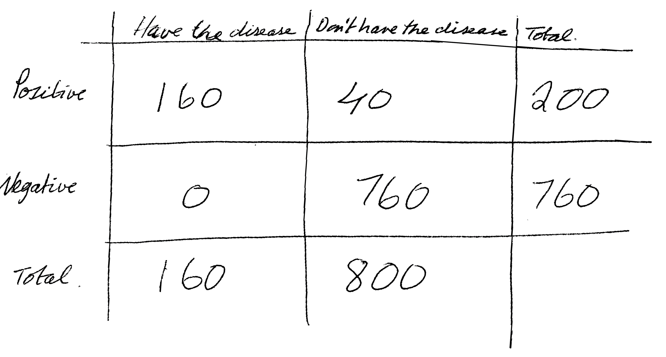
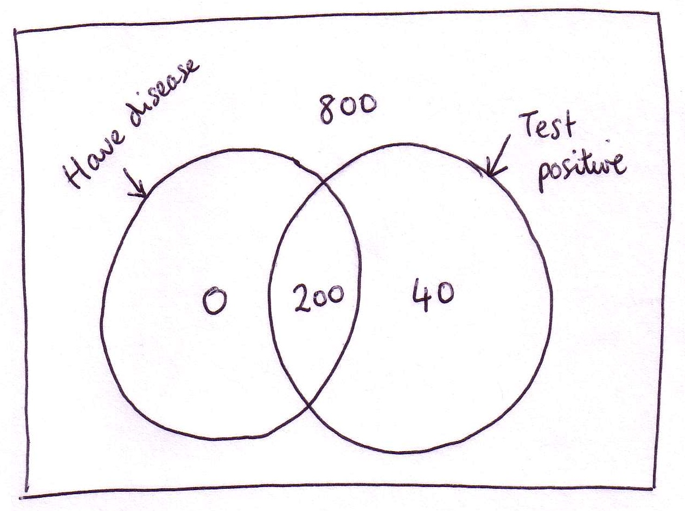
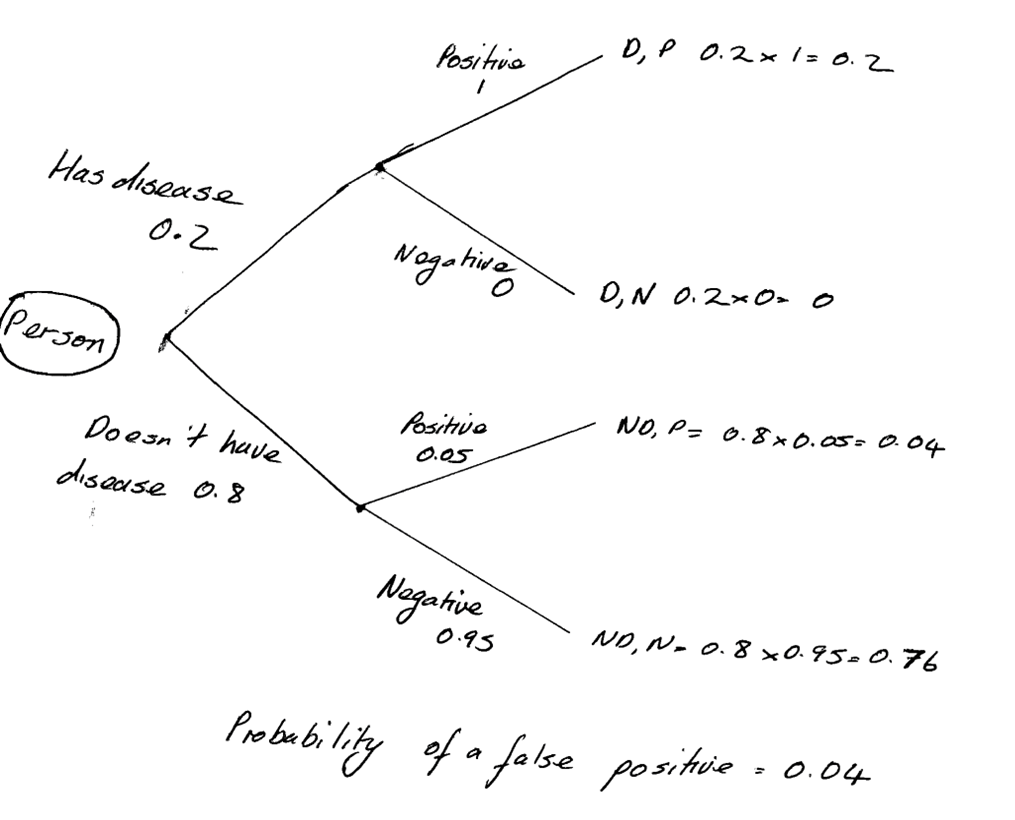
També podem trobar una activitat molt completa relacionada amb els tests mèdics, dels quals ja hi ha una activitat proposada a 3r d’ESO, al Mathematics Assessment Project titulada Representing Probabilities: Medical Testing en què s’analitzen els càlculs de diferents probabilitats agafant com a exemple l’ús de Diagrames d’arbre, Diagrames de Venn i Taules de contingència.

Font: Representing Probabilities: Medical Testing

Mathematics Assessment Project

Els jocs d’atzar haurien de ser activitats que generen experiències positives, tal com ho són quan juguem de petits, però de vegades es pot perdre el control i generar situacions molts complexes, saber #4.EST.PI.F.

Com a futurs adults, tindran molts jocs d’atzar al seu abast (loteries, el bingo, les apostes esportives, les màquines recreatives amb premi, el joc per Internet...) en què les opcions en línia van agafant cada vegada més força.

Seria interessant fer una reflexió a classe amb l’alumnat per ser conscients de les conseqüències que aquests jocs poden comportar.

Al web Canal Salut de la Generalitat de Catalunya trobem l’article El joc d’atzar i els jugadors amb una classificació del tipus de joc en funció de la manera d’afrontar-lo per part dels jugadors:

Joc saludable: la persona que juga està informada de quina és la probabilitat de guanyar o perdre, opcionalment, aposta quantitats moderades de diners i gaudeix de les experiències de joc amb situacions de risc baix.

Joc de risc: les persones que han experimentat dificultats a causa del joc, però majoritàriament han pogut controlar-se i evitar més conseqüències negatives, tenen més risc de caure en el joc problemàtic. Les persones en situació de risc han de ser especialment cauteloses a l’hora de jugar.

Joc problemàtic: les persones en situació de joc problemàtic destinen al joc més temps o diners dels que es poden permetre. Per a aquestes persones, jugar comporta conseqüències negatives. Per exemple, poden començar a jugar en solitari en lloc de fer-ho en companyia de les seves amistats, poden minimitzar o encobrir l’abast del seu joc o tenir discussions amb la família sobre dificultats financeres. Algunes d’aquestes persones poden jugar en el nivell problemàtic durant molt de temps i, finalment, acabar desenvolupant un problema més greu o bé tornar al joc recreatiu sense més complicacions.

Joc patològic: es considera que algú té una conducta patològica en relació amb el joc quan perd la llibertat de decidir si vol jugar o no i el joc passa a ser una necessitat prioritària, amb el deteriorament consegüent de la vida individual, familiar i social. Als problemes econòmics s’hi afegeixen complicacions en tots els àmbits: ruptures sentimentals, dificultats laborals, problemes en tota mena de relacions socials, un ampli ventall de problemes físics i emocionals, i, fins i tot, participació en activitats delictives i intents de suïcidi.

Per tant, és interessant analitzar alguns jocs d’atzar a classe i valorar-ne les probabilitats de guanyar, que sempre són ben poques. Així els alumnes no només han de tenir els coneixements per entendre el paper de l’atzar en cada situació, sinó que també han de fer servir el sentit crític en la valoració dels riscos que comporten aquests jocs.

Moltes vegades les promocions que es fan només mostren situacions en què els jugadors guanyen de forma ràpida i fàcil, tot i que no són les situacions habituals.

Una bona idea per revertir aquesta situació és la proposta de Anticasino d’Explorium, presentada a les Jornades d’ABEAM, en què l’objectiu era trobar les bones estratègies per aconseguir guanyar a la banca.

En el cas dels adolescents també hi ha situacions en què es poden veure involucrats, com per exemple les que detalla l’article Jocs d’apostes online en adolescents i joves de l’Hospital Universitari de Bellvitge, en què, a part de les apostes en línia en activitats esportives, jocs de cartes o jocs de casino, també es fa referència als mecanismes que s’utilitzen en els videojocs per aconseguir premis amb un fort component d’atzar, com ara les caixes botí, a canvi de moltes hores de joc o de diners. O alguns jocs que mostren directament ruletes amb premis o màquines escurabutxaques dintre del mateix entorn.

Es comenta també a l’article com «Es donen casos d’adolescents que han arribat a gastar milers d’euros buscant recompenses a través de les caixes botí. Alhora, s’ha demostrat la relació directa entre aquestes conductes anàlogues al joc d’aposta dins dels videojocs i la probabilitat de presentar conductes d’aposta en altres entorns.» Es recomana, per tant, «incloure el tema del joc amb diners a les escoles, estimular el pensament crític dels infants i els adolescents i treballar també en la detecció de conductes de risc des de diferents àmbits (sanitari, familiar i social, a través dels entorns esportius, d’oci, etc.).»