Variable

Sabers

Variables en l'expressió de relacions funcionals.
[ESS]

#ALG.RF
Distinció entre incògnites en equacions i variables en funcions.
#ALG.ID

#ALG.RF
Variables en el context estadístic.
#EST.DI

#EST.IN

Descripció i orientacions

Reflexions generals

A 2n cal destacar la introducció de les relacions funcionals en les seves diverses expressions (verbal, tabular, gràfica i algebraica) que representa un pas important en l’aprenentatge matemàtic i ofereix possibilitats d’aplicació a diferents àmbits molt riques. Això comporta la introducció de la idea de variable en el camp de les funcions, saber #2.ALG.VA.A.

A primer curs ja es va introduir el concepte de variable com a quantitat desconeguda o que pot adquirir diferents valors. Es tracta d’una definició àmplia que permet entendre la incògnita com un tipus de variable, però cal assenyalar que hi ha autors que prefereixen separar les dues idees. En la descripció i orientacions d’aquest mateix bloc corresponents a 1r, aquest aspecte es tracta amb una mica més de detall. Es consideri aquesta inclusió o no, des del punt de vista didàctic serà important distingir entre variable d’una funció i incògnita d’una equació. Per això resulta clau el saber #2.ALG.VA.B.

Comentaris sobre les connexions

Els sabers del bloc Variable tenen un caràcter molt conceptual i adquireixen tot el seu significat quan es posen en pràctica en el treball amb funcions ( #2.ALG.RF), en les equacions ( #2.ALG.ID) i en els estudis estadístics ( #2.EST.DI). Aquests coneixements són especialment valuosos quan s’apliquen a situacions contextualitzades.

Observacions sobre alguns sabers d’aquest bloc

Una funció relaciona dues variables de manera que, a cada valor d’una d’elles (anomenada variable independent) que pertanyi al seu domini, li fa correspondre un únic valor de l’altra (variable dependent). Per això la comprensió d’una relació funcional ha de partir de la identificació clara de les variables que es relacionen. En el cas de funcions en context, serà important donar significat a les variables tenint clares les magnituds que es representen, les unitats que s’empren per mesurar-les i els intervals de valors que poden adquirir. Per això el saber #2.ALG.VA.A, variables en l’expressió de relacions funcionals, haurà de ser tractat amb una cura especial. En aquesta mateixa línia, el saber #2.ALG.VA.B convida a posar atenció en la diferència entre les incògnites d’equacions i les variables de funcions que ja ha estat esmentada. Entendre bé aquesta diferència permetrà distingir millor entre equacions i funcions.

El saber #2.ALG.VA.C fa referència a les variables estadístiques qualitatives i quantitatives discretes (les quantitatives contínues es tractaran a 3r) i l’ús en situacions contextualitzades.

Comentaris sobre els sabers essencials i d’ampliació

La introducció de la idea de funció fa aconsellable que el saber #2.ALG.VA.A, variables en l’expressió de relacions funcionals, es consideri com a essencial en aquest bloc.

Recursos i activitats

Recursos i activitats generals per al bloc de sabers

La introducció a l’estudi de les funcions és un pas fonamental i convé assegurar una bona comprensió dels conceptes que es posen en joc en les diverses expressions de les relacions funcionals: textual, tabular, gràfica i algebraica. Representa la introducció d’un bagatge de nous conceptes que s’anirà desplegant al llarg de tota l’educació secundària i que podrà ser aplicat en contextos molt diversos. Per treballar les relacions funcionals, a tota l’ESO, pot ser molt útil el llibre El lenguaje de funciones y gráficas (Shell Centre for Mathematical Education, 1990), es tracta d’un clàssic absolutament actual ple de bones idees per a l’aula.

Recursos i activitats per treballar sabers concrets

A continuació, es presenten algunes idees sobre recursos i activitats d’aprenentatge que poden contribuir a l’adquisició dels sabers d’aquest bloc.

A. Variables en l'expressió de relacions funcionals. [ESS] #ALG.RF

En qualsevol situació que pugui ser estudiada per mitjà de relacions funcionals serà important identificar clarament les variables que es relacionen (la variable independent i la variable dependent) i les unitats en què es mesuren aquestes variables. Precisament el saber #2.ALG.VA.A se centra en aquest aspecte que ha de ser treballat, de manera integrada, dins d’activitats del bloc Relacions i funcions #2.ALG.RF. Tanmateix, a continuació, se suggereixen algunes idees (amb diferents punts de partida) molt focalitzades en el concepte de variable en situacions contextualitzades que es poden modelitzar per mitjà de relacions funcionals.

A partir d’una descripció textual

En una versió bàsica: La Isabel ha anat a fer una passejada amb bicicleta i ha mantingut una velocitat constant de 10 km/h fins que ha tornat a casa 36 minuts després de sortir. Quants quilòmetres ha fet en total? Quina distància havia recorregut al cap de 6 minuts de sortir? Al cap de 12 minuts de sortir? Al cap de 18 minuts de sortir? Al cap de 24 minuts de sortir? I al cap de 30 minuts? Podríeu fer una taula i un gràfic que reculli les respostes anteriors i descrigui el recorregut que ha fet la Isabel? Quines variables s’hauran de relacionar? En quines unitats es mesuren?

En una versió una mica més avançada: La Clara és aficionada a practicar bicicleta de muntanya. Avui ha sortit a fer un trajecte. Durant els 12 primers minuts ha mantingut una velocitat de 10 km/h. Després ha vingut un bon tram de lleugera baixada en què ha mantingut una velocitat constant de 15 km/h durant 16 minuts fins a arribar a casa seva. Mentre està netejant i guardant la bicicleta, el seu germà Artur li fa diverses preguntes: Quant de temps ha durat el trajecte? Quants quilòmetres ha fet en total? Quants quilòmetres havia fet al cap de 6 minuts de trajecte? Al cap de 12 minuts? Al cap de 16 minuts? Al cap de 20 minuts? Al cap de 24 minuts? I al cap de 28 minuts? Davant d’aquesta allau de preguntes, la Clara decideix fer una taula que les respongui i fins i tot un gràfic, per tal que l’Artur ho entengui millor. Quines variables haurà de relacionar? En quines unitats les mesurarà? Podríeu ajudar-la a fer la taula i el gràfic?

A partir d’una taula

En ascendir en globus, la distància a l’horitzó cada vegada és més gran. La taula següent relaciona l’altura de la cistella d’un globus (en metres ‒m‒) i la seva distància a l’horitzó (en quilòmetres ‒km‒):

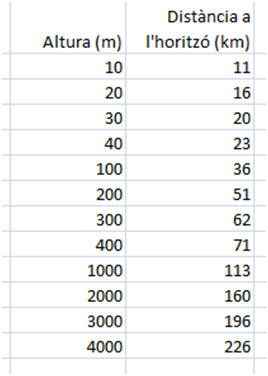
Quines variables es relacionen? Podríeu fer una representació gràfica aproximada? Quina interpretació es pot fer d’aquestes dades? Podríeu explicar-ho emprant, si cal, un dibuix?

A partir d’una consulta de dades

Es vol posar de manifest el canvi en les hores de sol diàries que es produeix al llarg de l’any. Quines variables cal relacionar? Quina seria la variable independent i quina seria la variable dependent? Amb quines unitats les mesuraríeu? Podríeu cercar les dades (per exemple en mitjans de premsa, almanacs, etc.)? Podríeu elaborar una representació gràfica aproximada? Podríeu escriure’n un comentari explicatiu?

A partir d’un gràfic

p> La Sofia ha fet una mica d’exercici físic, caminant/corrent des de casa seva, tal com es descriu en el gràfic següent:

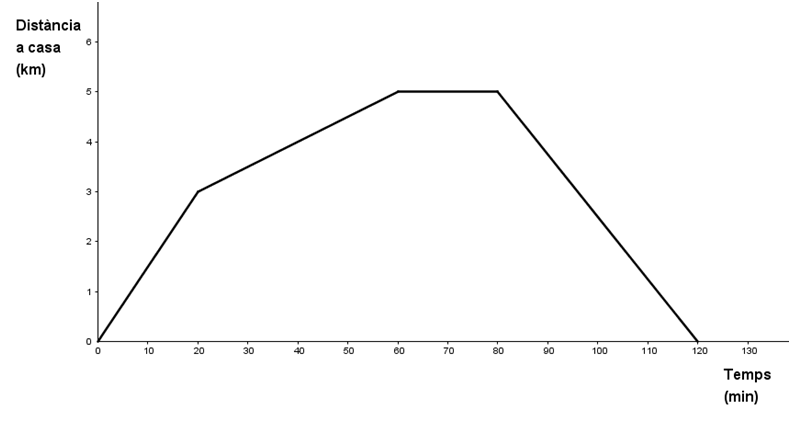
Quines variables relaciona el gràfic? Amb quines unitats es mesuren? Quant de temps la Sofia ha estat fora de casa? Quina ha estat la distància màxima a què ha arribat de casa seva? Podríeu descriure, a grans trets, el camí?

A partir d’una fórmula donada per una expressió algebraica

Hi ha diverses escales per mesurar la temperatura. Habitualment, a Europa s’utilitzen els graus Celsius (°C), però hi ha països, com els Estats Units, en què s’utilitzen els graus Fahrenheit (°F). Una mateixa temperatura s’expressarà com a c graus Celsius i com a f graus Fahrenheit. La relació entre c i f es descriu per l’expressió algebraica següent: f = 1,8c + 32.

Quines variables relaciona aquesta igualtat? Mesurades en quines unitats? A quants graus Fahrenheit correspon una temperatura de 0 graus Celsius? Podríeu fer una taula que indiqués el valor en graus Fahrenheit d’algunes temperatures expressades en graus Celsius? Podríeu fer un gràfic aproximat?

A partir d’una experiència

L’activitat s’inicia convidant l’alumnat que dibuixi i retalli un rectangle que tingui un perímetre de 60 cm. Un cop cada alumne/a hagi retallat el seu rectangle en cartolina (si pot ser de colors variats) demanarem que superposin tots els rectangles sobre el primer quadrant d’uns eixos cartesians tal com indica la figura següent:

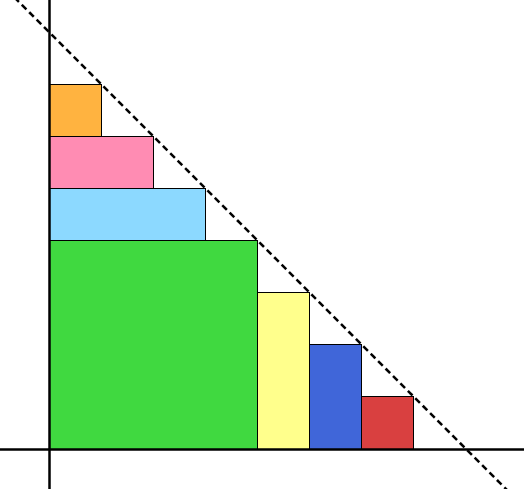
Observarem que els seus vèrtexs lliures són punts del gràfic d’una funció. Quina és la seva variable independent? I la seva variable dependent? Podríem determinar l’expressió algebraica d’aquesta funció?

Al bloc Relacions i funcions d’aquest mateix curs (#2.ALG.RF.C) hi ha una descripció detallada d’aquesta activitat, Rectangles d’igual perímetre i funcions afins, que també es troba a l’ARC.

B. Distinció entre incògnites en equacions i variables en funcions. #ALG.ID #ALG.RF

El saber #2.ALG.VA.B es consolidarà aprofitant oportunitats per assenyalar les diferències quan es resolguin equacions o es treballi amb funcions. Serà important tenir cura del llenguatge perquè l’alumnat faci servir adequadament els termes «equació», «incògnita», «funció» i «variable». La taula comparativa següent pot ajudar a distingir entre aquests termes:

	Incògnites en equacions	Variables en funcions
Definició	Valor desconegut per trobar.	Valor que pot variar.
Objectiu	Trobar, per mitjà de transformacions que assegurin l’equivalència de les expressions algebraiques, el valor de la incògnita que compleix l’equació.	Explorar relacions tot analitzant el canvi en la variable dependent quan canvia la variable independent.
Exemple de format	2x + 3 = 11 Només es compleix la igualtat si la x val 4.	f(x) = 2x + 3 y = 2x + 3 Per cada valor de x obtenim un valor de f(x) o de y.

C. Variables en el context estadístic. #EST.DI #EST.IN

El saber #2.ALG.VA.C es pot treballar portant a terme estudis estadístics propers als interessos de l’alumnat, duts a terme en equip i basats en observacions, enquestes, experiments o simulacions. Una de les primeres fases d’aquests estudis consisteix a determinar les variables estadístiques que s’analitzaran. És important identificar els tipus de variable presents en cada cas, ja que aquestes condicionen l’estudi estadístic i els diagrames utilitzats per presentar els resultats: qualitatives nominals (colors preferits, tipus d’avaries ateses en un garatge, etc.), qualitatives ordinals (nivells de satisfacció, qualificacions, etc.), quantitatives discretes (nombre de germans, nombre d’esports practicats, etc.) i quantitatives contínues (alçada, pes, etc.). Aquestes últimes es treballaran el pròxim curs.

Llicenciat sota la Llicència Creative Commons Reconeixement CompartirIgual 4.0