Sabers
En relació amb el saber #ALG.ID.A, tot i que ja es podria haver desenvolupat parcialment a 2n d’ESO, pensem que aquest curs és un bon moment per reflexionar sobre la diferència entre una igualtat que correspon a una identitat i la que correspon a una equació. En aquest sentit, la discussió sobre què és (i què no és) una igualtat com a + b = b + a $a + b = b + a$ i una altra com a + b = a·b $a + b = a\cdot b$, pot ser un bon punt de partida per dur a terme aquesta feina. Si trobem un contraexemple, quan hi sigui, veurem que no es tracta d’una identitat, però, en canvi, sí que és una equació (les solucions de la qual varien si parlem del domini dels enters positius, els enters o els racionals).
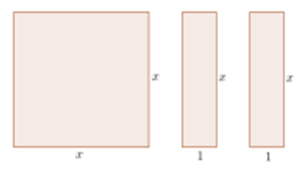
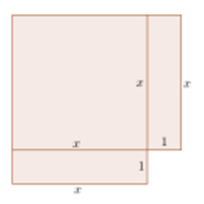
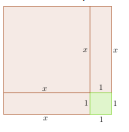
Pel que fa a les identitats dites «notables», cal trobar situacions en què tingui sentit aplicar-les. Moltes d’aquestes són de tipus geomètric i, ’per això, connectem aquest saber amb #3.ESP.VM, però també amb el sentit numèric, en concret amb #3.NUM.SO.
Finalment, aquest saber també inclou la factorització d’expressions algebraiques en casos senzills, que es poden relacionar amb la resolució d’equacions de segon grau (per exemple, les incompletes). En qualsevol cas, pot ser un bon moment per comparar la factorització d’expressions algebraiques amb la factorització de nombres. Aquesta part, però, es pot deixar per 4t si es vol factoritzar expressions de grau més gran que 2.
Pel que fa al saber #3.ALG.ID.B i al saber #3.ALG.ID.C, els hem separat, ja que entenem que la resolució d’equacions quadràtiques senzilles (incompletes) es pot fer emprant mètodes algebraics coneguts (aïllar o treure factor comú, segons els casos) i és una bona ocasió per tal que l’alumnat pugui resoldre-les sense «aplicar» fórmules. Ens referim a equacions senzilles com (x2 = 4), i incompletes com x2 – 9 = 0, x2 - 3x = 0, o bé (x - 1)2 = 9. Per això, entenem que el saber #3.ALG.ID.B ha de precedir el saber #3.ALG.ID.C i no a l’inrevés.
Quant al saber #3.ALG.ID.E, l’ús de problemes contextualitzats que porten a resoldre equacions quadràtiques senzilles, és rellevant assenyalar que hi ha equacions quadràtiques, com y = 1/2 k x2, la resolució de les quals adquireix rellevància quan es constata que nombroses lleis científiques tenen aquesta estructura, com la llei de la caiguda dels cossos, s = 1/2 gt2, l’energia cinètica, Ec = 1/2 mv2, o la calor despresa per una resistència en funció de la intensitat del corrent Q = 1/2 RI2. Aquests exemples ens permeten entendre que les funcions matemàtiques són generalitzacions de les lleis científiques i que l’expressió algebraica d’una funció expressada per mitjà de variables abstractes, x, y, és una abstracció de l’expressió d’una llei física també amb dues variables, però concretes (espai-temps, energia-velocitat, calor-intensitat). Podem trobar aquesta reflexió en el llibre d’Aleksandrov i altres La matemática, su contenido, sus métodos y su significado, Alianza Editorial (1973).
També en relació amb el saber #3.ALG.ID.E, com ja dèiem en cursos anteriors, és important tenir en compte la problemàtica de l’ús de contextos. Puig Adam, en el seu decàleg (1960) diu: «No oblidar l’origen concret de les matemàtiques i els processos històrics de la seva evolució». Uns anys abans, Lobachevski (1792-1856) havia afirmat: «No hi ha cap branca de les matemàtiques, per abstracta que sigui, que no es pugui aplicar algun dia a l’estudi dels fenòmens del món real». Totes dues cites, des de punts de vista ben diferents, apel·len a la relació entre les matemàtiques i els diferents contextos.
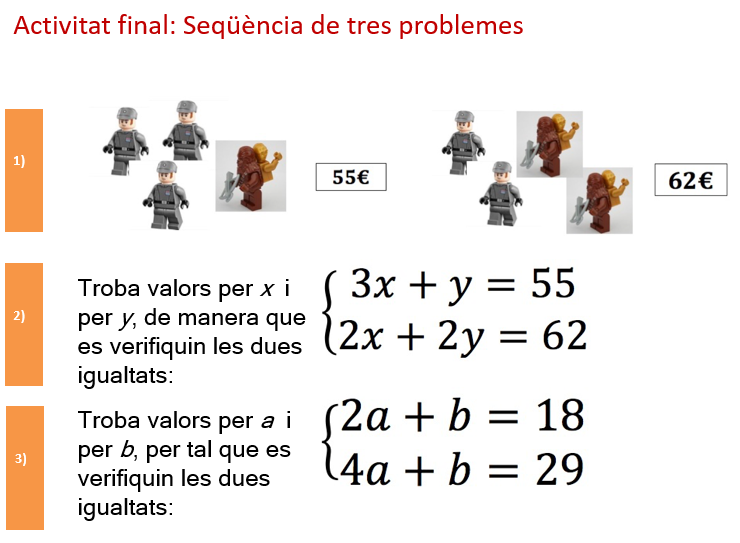
El saber #3.ALG.ID.F, resolució de problemes contextualitzats per mitjà de sistemes de dues equacions lineals amb dues incògnites, mereix un comentari detallat: ens trobem davant d’un saber que l’alumnat pot construir realment partint de problemes, resolent primer sense l’ús del llenguatge algebraic (manipulant el llenguatge icònic) i, posteriorment, per mitjà d’una connexió entre representacions (icònica i algebraica), traspassar allò que s’ha fet en el llenguatge icònic al llenguatge algebraic per tal de descobrir un dels mètodes més importants de la resolució de sistemes lineals com és el de reducció. Es pot trobar informació sobre com les connexions ens ajuden a construir coneixement matemàtic a l’article de de la Fuente, A. i Deulofeu, J. (2022), «Uso de las conexiones entre representaciones por parte del profesor en la construcción del lenguaje algebraico», Bolema, vol. 36, núm. 72, p. 389-410. També a de la Fuente, A. (2022), «Aprender a usar el álgebra en secundaria mediante la resolución de problemas», SUMA, núm. 99, p. 49-60.
El saber #3.ALG.ID.G i el saber #3.ALG.ID.H completen el treball amb sistemes de dues equacions lineals amb dues incògnites iniciat en el saber #3.ALG.ID.F. En el primer cas, la representació gràfica dona significat a cadascuna de les equacions, com a expressions de funcions, i a la solució del sistema (quan n’hi ha) com la intersecció de les dues rectes. També es poden connectar les posicions relatives de les dues rectes (coincidents, secants o paral·leles) amb les solucions del sistema (compatible indeterminat ‒infinites solucions‒, compatible determinat ‒una solució‒, incompatible ‒cap solució‒). Amb el saber #ALG.ID.H es completa el treball amb la resolució de problemes contextualitzats per mitjà de sistemes d’equacions lineals. Recordem que sempre que treballem amb situacions contextualitzades és important no perdre el significat del context en el procés de resolució.
Rellevància i tipologia dels contextos
En l’ensenyament de les matemàtiques, les característiques de les activitats d’aprenentatge són un punt clau. Si aquestes activitats tenen com a objectiu la construcció de sabers matemàtics de naturalesa abstracta, cal partir de concrecions d’aquests sabers. D’altra banda, si el que es vol és mostrar les diferents utilitats de les matemàtiques i aplicar-les per resoldre problemes diversos, també cal concretar aquells contextos en què és possible i té sentit aplicar les matemàtiques del currículum. És precisament en l’aplicació de sabers a contextos diferents on es manifesta una part important de la competència matemàtica.
Per tant, en el procés d’aprenentatge matemàtic, hi ha com a mínim dos moments en què els contextos són rellevants:
- En l’inici del procés, d’una banda per interessar a l’alumnat, creant reptes que vulgui intentar resoldre, i, de l’altra, per proporcionar-li un suport concret i significatiu per construir nou coneixement.
- En la part final del procés, per mostrar que les matemàtiques són útils per analitzar i resoldre situacions d’àmbits molt diversos i, al mateix temps, per consolidar i aplicar els aprenentatges duts a terme.
Per tal d’aportar orientacions sobre quins contextos poden ser els més adequats per introduir a les classes de matemàtiques, pensem que cal anar més enllà de les classificacions generals com els anomenats contextos quotidians o contextos reals, expressions que semblen incloure tot allò que no és directament matemàtic, ja que, si no precisem una mica, podria semblar que tot context no matemàtic pot ser adequat. Presentem, sense ànim d’exhaustivitat, una tipologia de contextos:
Context proper a l’alumne. Interessos, vivències i necessitats dels alumnes. Són aquelles situacions que interessen a l’alumnat perquè els afecten directament. S’inclouen aquí les situacions en què es reclama a l’alumne una participació directa i vivencial (teatralitzacions, jocs de rol, etc.) i també les experimentacions a partir de materials manipulatius. Aquest context se situa, majoritàriament, en la part introductòria del procés d’aprenentatge.
Context quotidià. Entorn social, local, laboral i cultural proper a l’alumnat. Són situacions que ’es poden comprendre per la proximitat i, per aquest motiu, és important analitzar-les i conèixer-les emprant les matemàtiques. Són especialment adequades aquelles que, a més de socialment rellevants, s’han produït en un moment proper al del treball a classe (eleccions, fenòmens apareguts en mitjans de comunicació, actes culturals, esportius etc.)Context històric. Molts dels sabers del currículum de l’ESO van ser creats fa molts segles per resoldre problemes que tenen sentit quan s’emmarquen en l’època en què es van desenvolupar. Utilitzar aquests problemes i les solucions originals pot servir per donar sentit als sabers involucrats, veure’n l’origen i també conèixer altres maneres de fer matemàtiques d’acord amb els coneixements del seu temps.
Context lúdic. Les recreacions matemàtiques, els reptes i els jocs són un context molt extens que es pot relacionar amb la majoria de sabers matemàtics. Tot i que podria entrar dins del context quotidià (jugar és una activitat humana rellevant i adequada a l’adolescència) és molt ampli i permet dissenyar activitats de durada molt diversa. La idea de repte i l’interès intrínsec de moltes recreacions i jocs és un dels punts clau de la rellevància d’aquest context.
Context científic i tecnològic. Les relacions entre les diferents ciències experimentals, ciències de la salut i la tecnologia amb les matemàtiques són moltes i, per tant, els contextos científics poden ser apropiats tant per construir conceptes matemàtics i comparar-los amb els seus equivalents en altres ciències, com també per aplicar sabers matemàtics ja construïts. Cal tenir en compte que tant aquest context com els dos següents tenen relació amb altres matèries del currículum, per la qual cosa és adequat introduir-los d’acord amb el treball realitzat en les matèries relacionades.
Context social. Moltes problemàtiques de les ciències socials (geografia, història, economia etc.) i del món d’avui dia (desigualtats, guerres, pandèmies, canvi climàtic etc.) necessiten les matemàtiques per ser analitzades i, al mateix temps, ajuden a donar sentit a molts sabers, especialment el sentit estocàstic.
Context humanístic. L’art, la fotografia, la música, la literatura i la resta de disciplines dites humanístiques comparteixen totes elles relacions amb les matemàtiques, en els dos sentits esmentats: ajudar a construir conceptes matemàtics per mitjà de plasmacions artístiques i proporcionar activitats d’aplicació de les matemàtiques en l’anàlisi de problemàtiques d’aquestes disciplines.
Context matemàtic. Fer matemàtiques és, moltes vegades, treballar en el context pròpiament matemàtic i en les connexions internes que hi ha entre els diferents sabers; mantenir la idea de repte, que porta a voler fer allò que es proposa, i basar-se en aquells sabers que ja poden considerar-se concrecions, per tal de construir-ne d’altres.
Entenem que una tipologia de contextos com aquesta pot ajudar a trobar exemples de situacions per ser treballades a l’aula, procurar que els contextos abastin l’ampli ventall proporcionat i també ser compartides amb el treball en altres matèries, sempre tenint en compte les característiques i els interessos de l’alumnat.