Reflexions generals
Tal com es comenta als documents dels cursos anteriors, un dels conceptes matemàtics fonamentals que s’estudien al llarg de l’etapa de secundària és el de funció. Les funcions ens permeten estudiar fenòmens de canvi i relacions entre variables, per la qual cosa són una part fonamental en la modelització de situacions contextualitzades ( #4.ALG.MM) i permeten establir connexions amb altres camps de les ciències o les ciències socials.
Ara, a 4t d’ESO, s’ha de seguir el camí iniciat als cursos anteriors, partint del fet que les funcions proporcionen contextos per pensar en les relacions de canvi i procurar que l’alumnat no es quedi amb una visió poc profunda de les funcions que limiti el concepte de funció a una fórmula o al seguiment de pautes per aconseguir un gràfic. Al llarg de tot aquest bloc Relacions i funcions, és important continuar tenint en compte, tal com es proposa també als cursos anteriors, el bloc Variable, #4.ALG.VA, que cal anar treballant conjuntament donada l’estreta relació que hi té.
Si a 2n d’ESO es proposava començar l’estudi de funcions lineals i afins i, a 3r, se suggeria continuar amb l’estudi de relacions de proporcionalitat inversa i quadràtiques analitzant aquestes relacions, per començar a construir famílies de funcions a partir de les característiques, ara a 4t, es recomana seguir la mateixa línia amb les funcions exponencials. Una eina que hem de tenir present en l’estudi d’aquestes característiques són els programes de geometria dinàmica, que poden ajudar a millorar-ne la comprensió conceptual.
Comentaris sobre les connexions
Com ja s’ha comentat a l’apartat Reflexions generals, és evident la connexió amb el bloc Variable, #4.ALG.VA, i també amb el bloc Igualtat i desigualtat, #4.ALG.ID, ja que no es pot deslligar l’estudi de les característiques de les funcions de la resolució d’equacions, vist tant des del punt de vista analític com gràfic.
A través de les funcions, podem descriure molts fenòmens, ja siguin quotidians, d’altres àmbits de coneixement o fins i tot de les matemàtiques mateixes. Estem parlant, per tant, de modelització matemàtica i establint connexions directes amb els blocs #4.ALG.MM i #4.ESP.VM. També s’estableixen connexions amb #4.ESP.LS quan es treballa l’efecte del pendent i l’ordenada a l’origen de les funcions lineals i afins.
Observacions sobre alguns sabers d’aquest bloc
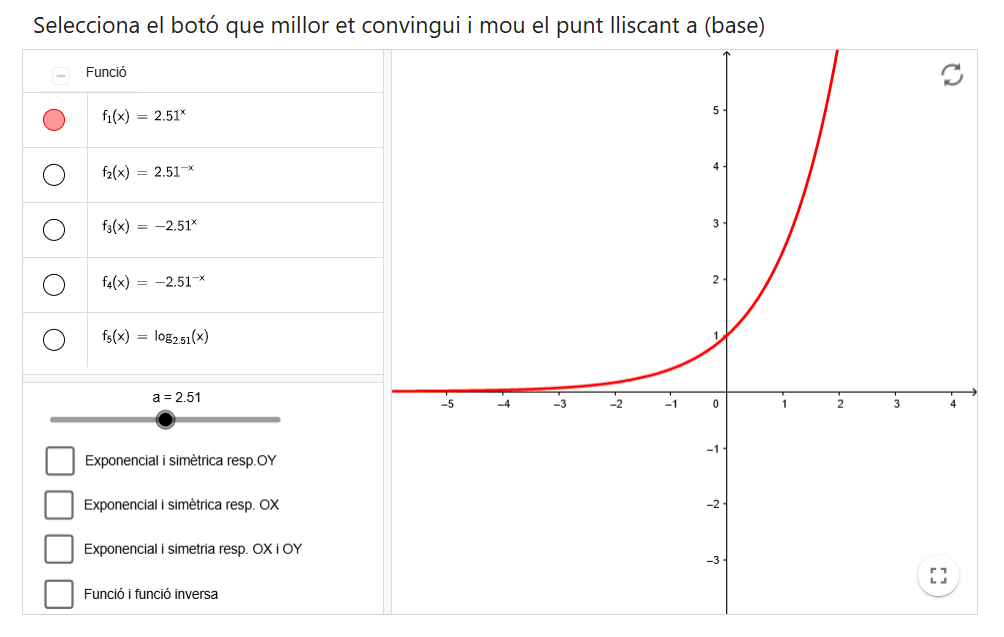
L’estudi de la funció exponencial, saber #4.ALG.RF.B, proporciona una comprensió essencial d’un tipus de funcions que són àmpliament utilitzades en ciències, tecnologia i altres camps. La comprensió de les seves propietats, com ara l’evolució del creixement i el decreixement exponencial, ajuda a aprofundir en la comprensió conceptual de les propietats de les funcions i a enfortir els coneixements sobre càlcul i àlgebra.
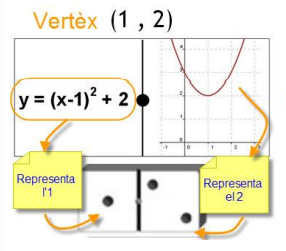
Es continua treballant el saber #4.ALG.RF.E, introduït a 3r, per tal d’aportar a la comprensió conceptual de la idea de funció. Les gràfiques permeten veure intuïtivament com es comporta una funció. Entendre les propietats com el creixement, el decreixement, els màxims, els mínims, les simetries, etc. a partir de la gràfica, ajuda a visualitzar com les funcions canvien i a identificar patrons ràpidament. D’altra banda, treballant els gràfics de les funcions, l’alumnat desenvolupa habilitats per analitzar i interpretar informació de manera crítica.
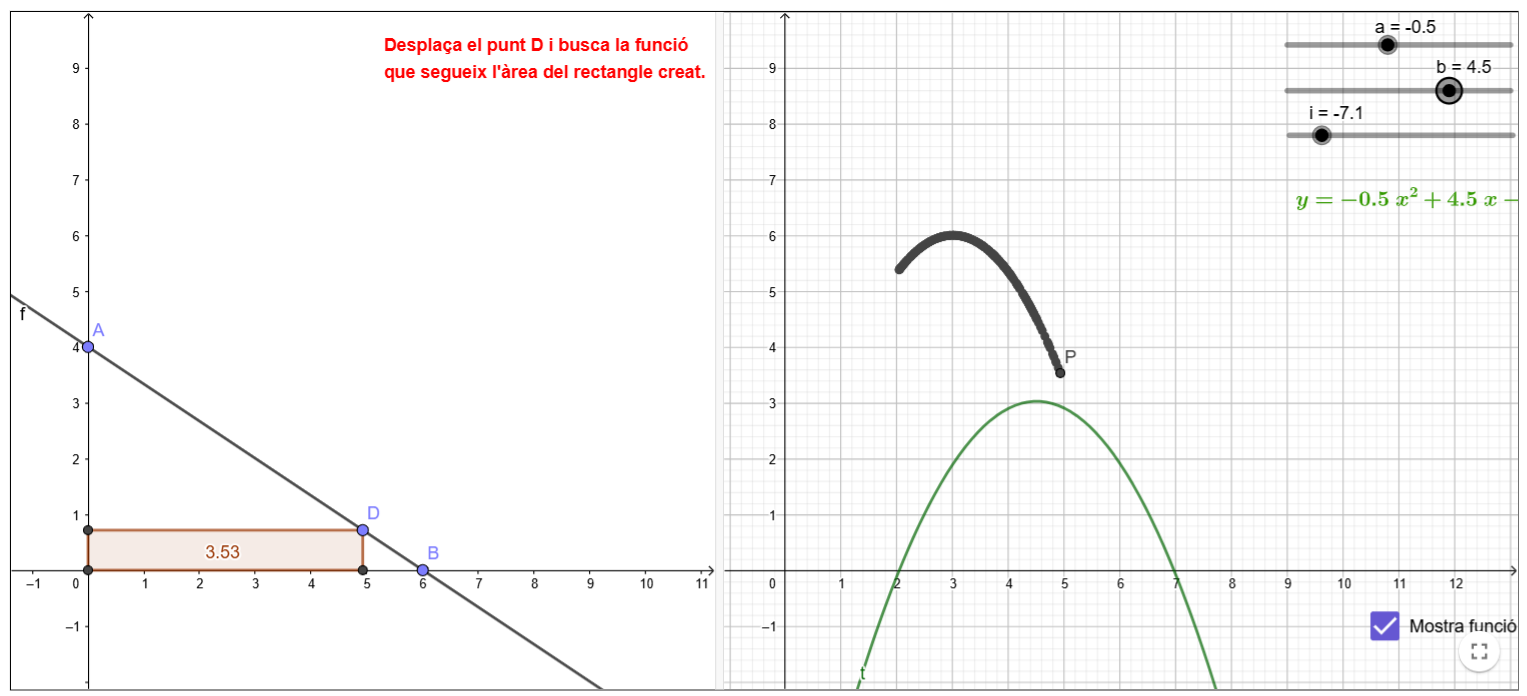
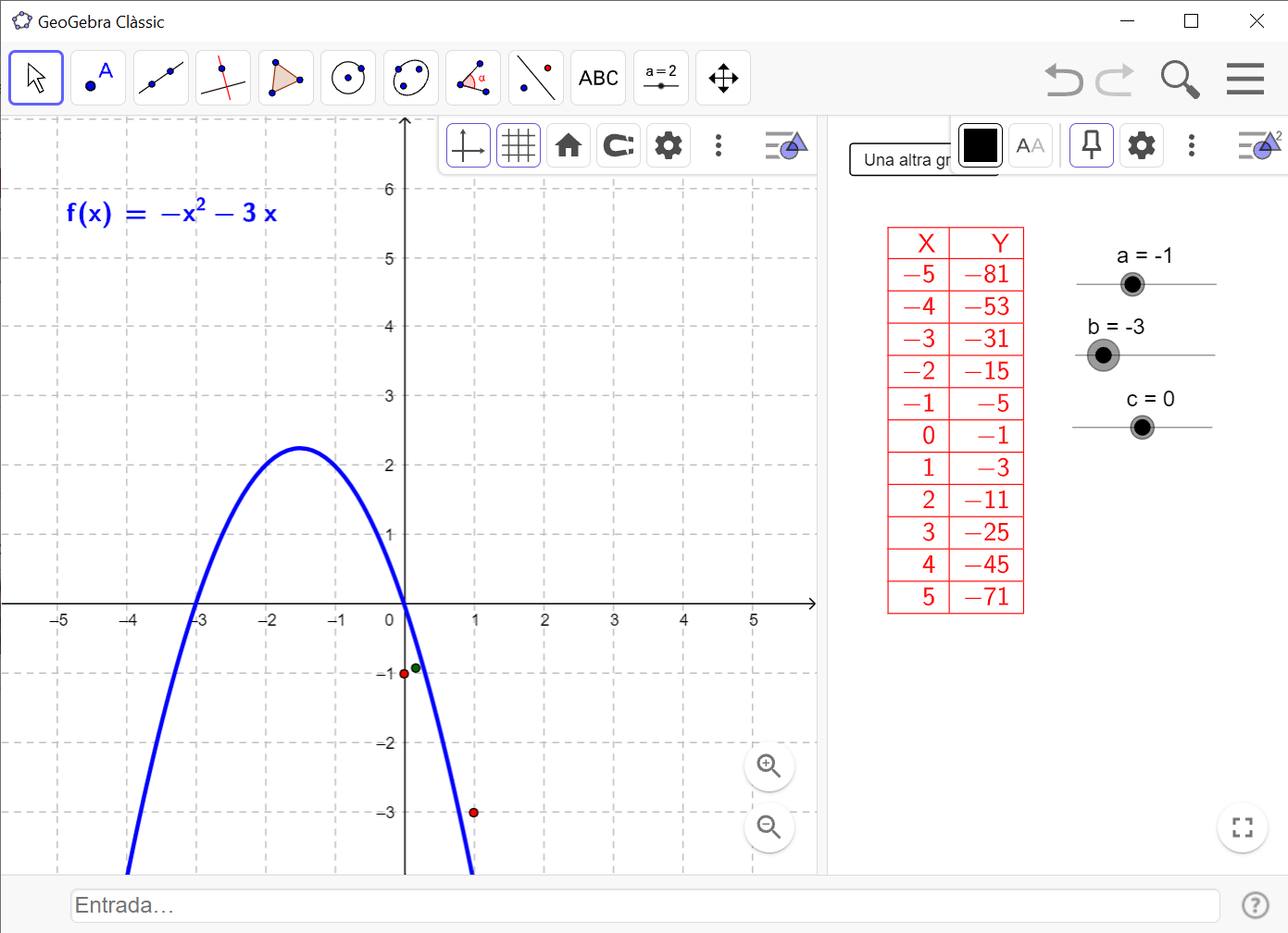
Respecte al saber #4.ALG.RF.F, els recursos digitals de geometria dinàmica poden ajudar l’alumnat a veure clarament com les relacions entre les variables es modifiquen de manera immediata quan canvien certs valors. Aquesta interactivitat facilita la comprensió i permet l’estudi de moltes situacions de canvi: com canvia el gràfic d’una funció quan modifiquem els coeficients d’una equació, com es comporten les funcions en diferents intervals del seu domini o com es transformen les gràfiques a mesura que es modifiquen certs paràmetres, per exemple. Aquests recursos permeten que l’alumnat vegi i experimenti amb els conceptes de manera més intuïtiva, ajudant a millorar la comprensió de les relacions funcionals.
Respecte al saber #4.ALG.RF.G, anàlogament als cursos anteriors, es pretén que l’alumnat sigui capaç d’extreure informació d’una funció donada a través de qualsevol de les representacions possibles. A l’hora de fer-ho a partir de gràfics, és interessant treballar també amb situacions no quantificades per centrar el focus en els diferents tipus de variació d’una funció, i no només en els valors concrets que pren.
Comentaris sobre els sabers essencials i d’ampliació
Tenint en compte que és l’últim curs de l’educació obligatòria i veient el nivell d’abstracció necessari per treballar tots els conceptes del bloc, s’ha considerat que no s’havia de posar cap saber essencial malgrat que es considerin tots ells molt importants per a tots els alumnes, especialment per a aquells que pretenen continuar el seu camí acadèmic fent batxillerat.
Com que les funcions definides a trossos conceptualment són diferents de la resta i, per definició, incorporen totes les altres, s’ha decidit que aquest saber s’havia de considerar d’ampliació. Malgrat aquesta consideració, es poden trobar contextos que involucrin les funcions a trossos que permeten treballar aquest tipus de funcions senzillament i fent que s’entengui bé el concepte.