Fitxa de colors

L’activitat Fitxa de colors, inclosa a l’ARC, té com a objectiu explicar una manera estructurada de plantejar el problema general de la combinatòria. L’activitat busca fomentar el raonament sobre els criteris de formació d’agrupacions i facilitar la deducció de fórmules de recompte. Per assolir aquests objectius, es treballa amb l’ús de fitxes de colors com a recurs manipulatiu i visual.

Per desenvolupar l’activitat, es formen grups de tres alumnes, i a cada equip se li dona quatre pilons de fitxes, cadascun d’un color diferent. Per a alguns exercicis serà necessari utilitzar un piló addicional, mentre que en altres s’haurà de prescindir d’un dels pilons.

Tot seguit, se’ls demana: «Formeu tots els grups possibles amb 3 fitxes». L’enunciat d’aquesta activitat és intencionadament ambigu per provocar que l’alumnat es qüestioni la necessitat d’establir criteris com ara si importa o no l’ordre i si es permet o no la repetició de fitxes.

Es recomana que el professorat deixi que els diferents grups reflexionin durant una estona sobre aquestes qüestions abans d’intervenir. Un cop tots els grups ho hagin analitzat, es pot introduir la idea que, segons la resposta que es doni a aquestes dues preguntes, es poden obtenir diferents tipus d’agrupacions, cadascuna amb el seu nom específic: variacions, variacions amb repetició, permutacions i combinacions.

Com a primer exercici, es demana als grups que formin agrupacions «tenint en compte que l’ordre importa i que no es poden repetir fitxes». L’alumnat anirà treballant fins que ja no trobi més agrupacions (n’hi ha 24, tot i que no ho sàpiga d’entrada). És important que els alumnes discuteixin quines agrupacions sobren en alguns casos i quines falten en altres. Aquesta reflexió els portarà a establir que hi ha exactament 24 agrupacions possibles.

Arribats a aquest punt, se’ls pot preguntar: «Com sabeu que no n’hi ha més?». Aquesta pregunta conduirà l’alumnat a establir i explicar uns criteris de construcció, a partir dels quals es podrà deduir fàcilment la fórmula de les variacions.

Un cop completat aquest exercici, es repetirà el procés amb altres tipus d’agrupacions. Si considerem que «m» és el nombre de colors diferents disponibles en cada cas, i «n» és el nombre de fitxes que formen cada agrupació, un possible ordre d’activitats seria el següent:

\(m=4\), \(n=3\)_, importa l’ordre, no es poden repetir: \(V_4^3=24\)

\(m=4\), \(n=2\), importa l’ordre, no es poden repetir: \(V_4^2=12\)

\(m=5\), \(n=2\), importa l’ordre, no es poden repetir: \(V_5^2=20\)

\(m=3\), \(n=3\), importa l’ordre, no es poden repetir (Permutacions): \(P_3=6\)

\(m=4\), \(n=4\), importa l’ordre, no es poden repetir (Permutacions): \(P_4=24\)

\(m=4\), \(n=2\), importa l’ordre, sí que es poden repetir: \(VR_4^2=16\)

\(m=3\), \(n=2\), importa l’ordre, sí que es poden repetir: \(VR_3^2=9\)

El cas de les combinacions és una mica més difícil d’introduir. Comencem construint totes les agrupacions possibles segons les variacions: \(V_4^3\)

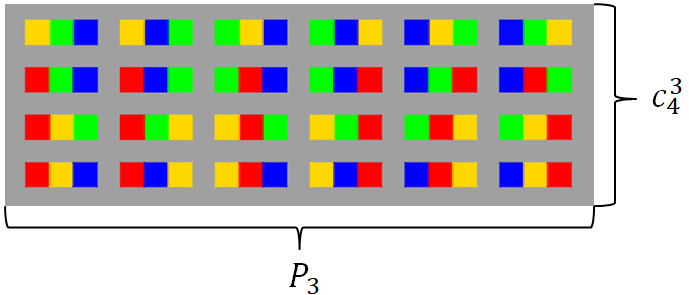
Un cop fet això, sobre la taula, les reordenem de manera que formin un rectangle. En aquest rectangle, cada fila inclou totes les agrupacions de fitxes que tenen els mateixos tres colors.

La base del rectangle tindrà un nombre d’elements corresponent a: \(P_3\)

Cada fila representarà una combinació, i l’altura del rectangle serà: \(C_4^3\)

L’àrea total del rectangle correspon a la totalitat de les agrupacions: \(V_4^3\)

A partir d’aquí, podem establir la relació: \(V_4^3=P_3\cdot C_4^3\)

Aïllant les combinacions, obtenim la fórmula en el cas concret: \(C_4^3=\displaystyle\frac{V_4^3}{P_3}\)

Aquest enfocament és fàcilment generalitzable i ens permet deduir la fórmula de les combinacions en el cas general.

Quin cadenat és més segur?

Una altra activitat que també treballa el saber #4.NUM.CO.A és la plantejada a la situació d’aprenentatge Quin cadenat és més segur?, que proposen Berta Barquero, Marianna Bosch i Susana Vásquez. Es parteix d’una qüestió sobre la seguretat dels cadenats per il·lustrar la proposta dels recorreguts d’estudi i investigació com a metodologia per al disseny i implementació de situacions d’aprenentatge.

Partint d’una situació real i significativa, l’activitat permet treballar conceptes com el comptatge i la combinatòria. L’alumnat ha de determinar el nombre de combinacions possibles per a diferents tipus de cadenats, aplicant la regla del producte: multiplicar el nombre de possibilitats de cada roda. Això introdueix conceptes clau, com les variacions amb repetició, ja que els codis permeten repetir dígits i l’ordre és important. Aquest enfocament promou la comprensió de les matemàtiques de manera aplicada i contextualitzada.

L’activitat també ajuda a reflexionar sobre com canvia la seguretat dels cadenats segons el nombre de rodes o dígits, i fomenta el raonament crític i la capacitat d’extrapolació. A més, connecta amb la probabilitat, calculant la probabilitat d’encertar el codi per atzar. És una eina didàctica ideal per a 4t d’ESO, ja que combina la teoria de la combinatòria amb l’aprenentatge actiu i interdisciplinari, de manera que millora la resolució de problemes i el pensament matemàtic en un context pràctic.

En el cicle de conferències de perspectives matemàtiques del CREAMAT, les autores van explicar l’activitat Com dissenyar i implementar situacions d’aprenentatge? El cas dels cadenats a segon cicle de l’ESO.

Línies poligonals

L’activitat Línies poligonals proposada per Anton Aubanell a l’ARC aplica conceptes de combinatòria en un context geomètric i ofereix múltiples possibilitats educatives en l’àmbit de l’ESO, concretament pot resultar útil per treballar el saber #4.NUM.CO.A.

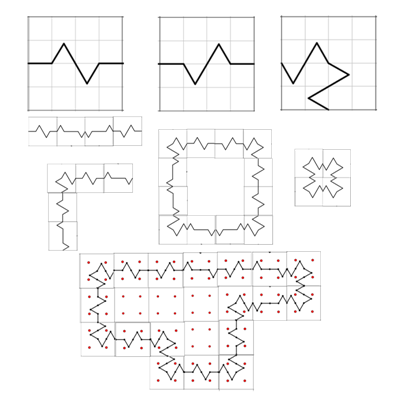
En aquesta activitat l’alumnat ha de calcular el nombre de línies possibles combinant diverses peces geomètriques, amb diferents orientacions i moviments. Això implica aplicar la regla del producte per comptar les configuracions totals i considerar restriccions (com crear circuits tancats). També hi ha la possibilitat de programar-ho amb Snap! o Scratch.

Aquest enfocament reforça conceptes de comptatge treballats a 4t d’ESO connectant-los amb geometria i contextos pràctics. A més, l’ús d’eines digitals com GeoGebra facilita la verificació visual dels càlculs i potencia l’aprenentatge actiu.