Sabers
- Ús de la proporcionalitat numèrica com a model matemàtic de situacions contextualitzades.
#NUM.RP
- Anàlisi de les solucions d'un problema, presa de decisions en conseqüència i formulació de prediccions, si escau.
[ESS]
Les matemàtiques ens permeten entendre millor el món i prendre decisions. La modelització matemàtica implica la construcció de models matemàtics per abordar situacions sobre fenòmens naturals i socials, i en què l’elecció de les matemàtiques rellevants, per donar resposta a la situació, forma part del procés de resolució.
Segons expliquen Solar, Deulofeu i Azcárate a l’article Competencia de modelización de gráficas funcionales (Solar et al., 2015):
La modelització és el conjunt de fases necessàries per resoldre un problema provinent d’una situació real per mitjà d’un model matemàtic.
Hi ha moltes versions del cicle de modelització, però totes contenen els mateixos elements essencials i etapes. Els autors citats anteriorment ens proposen el següent:
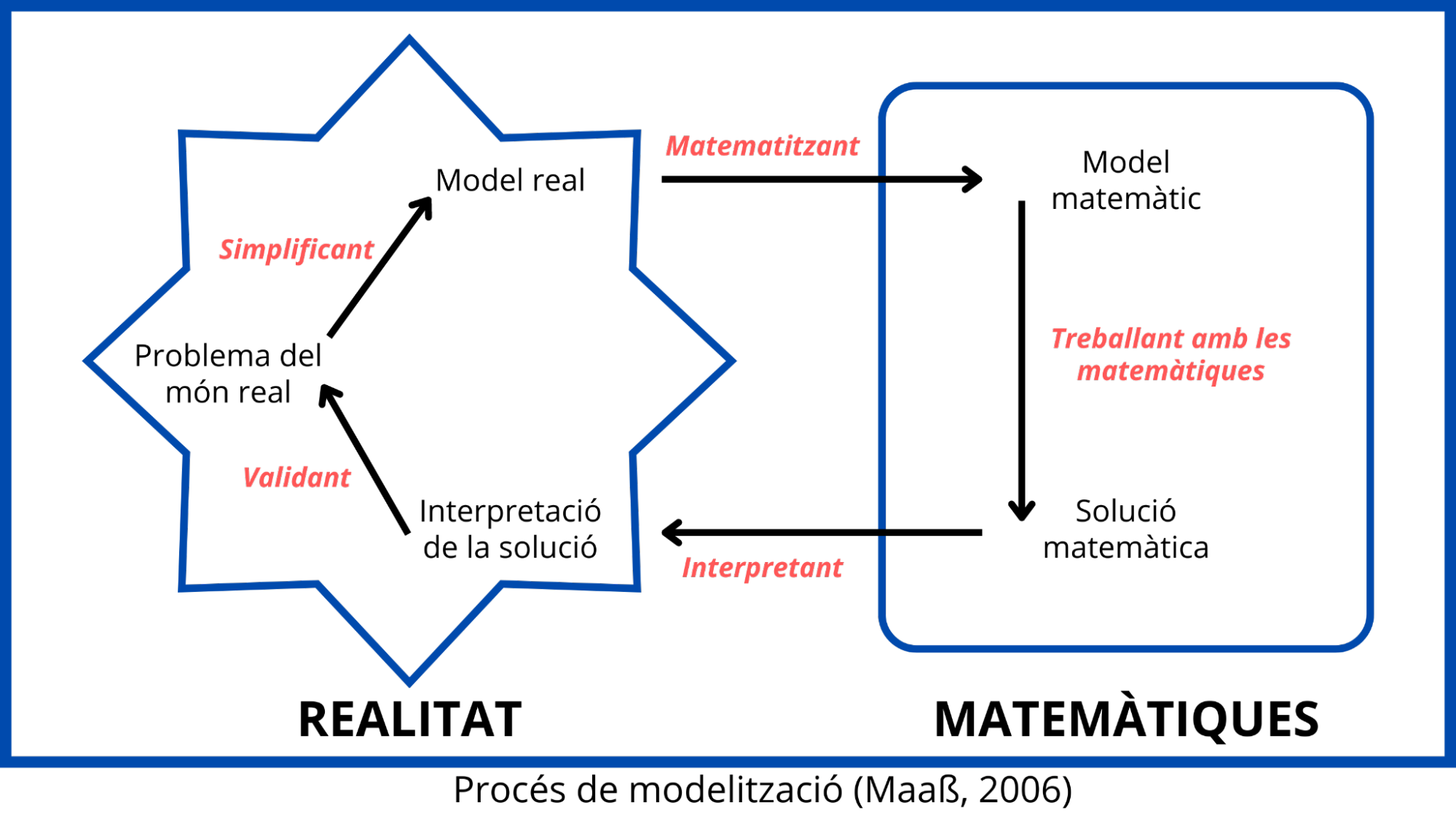
El procés de modelització matemàtica no s’ha de confondre amb l’ús d’un model per representar o resoldre un problema que no requereix tot el procés.
El procés de modelitzar matemàticament suposa un repte per a l’alumnat i, de vegades, amb certa dificultat per la falta de pràctica. Alguns aspectes que el professorat podem tenir en compte són, per exemple, treballar l’organització de la feina, recordar que tenen calculadores i programes informàtics a la seva disposició i, quan algun grup es quedi encallat o vagi en una direcció poc desitjada, fer preguntes del tipus:
La tecnologia i la creativitat tenen un paper important quan estem fent modelització matemàtica. A l’hora de crear models, les eines tecnològiques (programes de geometria dinàmica, fulls de càlcul, calculadores…) ens poden ser de gran ajuda, ja que ens permeten avaluar diferents opcions, comparar-les i fer prediccions. D’altra banda, el procés de formular un model, representar-lo i analitzar-lo depèn de l’experiència i de la creativitat que s’ha anat adquirint al llarg dels anys. Per aquest motiu, és important no deixar per a més endavant aquest bloc i començar a treballar-lo a 1r d’ESO.
Cal fer esment de l’estreta relació d’aquest bloc amb el saber #SOE.CE.M, Apreciació de l’interès dels processos de modelització com a forma atractiva d’enllaçar les matemàtiques amb la realitat sobre la qual es vol actuar, del sentit socioemocional.
S’han destacat dues connexions molt evidents. D’una banda, el saber #1.ALG.MM.A està relacionat de forma natural amb el bloc de raonament proporcional del sentit numèric, ja que el que es pretén és modelitzar situacions contextualitzades a través de la proporcionalitat numèrica. D’altra banda, el saber #1.ALG.MM.B apel·la directament al sentit socioemocional. L’anàlisi de les solucions d’un problema permet identificar els errors (propis o dels companys) i fer aportacions constructives per trobar alternatives. La presa de decisions implica col·laborar activament amb els companys per arribar a acords.
Amb el treball del saber #1.ALG.MM.A es poden posar en joc moltes idees matemàtiques: fraccions, raons, proporcions, operacions, etc. A més, si es demana a l’alumnat que expliqui el model i les estratègies que han seguit al llarg del procés, es dona l’oportunitat d’enriquir el treball dut a terme escoltant les idees i propostes dels companys i companyes de classe.
En el bloc Model matemàtic, s’ha destacat el saber #1.ALG.MM.B (Anàlisi de les solucions d’un problema, presa de decisions en conseqüència i formulació de prediccions, si escau) com a essencial, ja que es considera fonamental en el procés de resolució de problemes.
Apreciació de l’interès dels processos de modelització com a forma atractiva d’enllaçar les matemàtiques amb la realitat sobre la qual es vol actuar.
Ús de la proporcionalitat numèrica com a model matemàtic de situacions contextualitzades.
Anàlisi de les solucions d'un problema, presa de decisions en conseqüència i formulació de prediccions, si escau.
Un tipus de tasques en què el treball de modelització matemàtica pot encaixar de forma òptima són els projectes. El CREAMAT té una campanya anomenada Matemàtiques i projectes en què es poden trobar molts exemples detallats amb tots els materials necessaris per dur-los a terme a l’aula.
Les tres propostes que es presentaran tot seguit ens serviran per treballar els dos sabers d’aquest bloc: #1.ALG.MM.A i #1.ALG.MM.B.
En primer lloc, tenim l’activitat Anem a fer llimonada del professor Lluís Mora. L’alumnat haurà de decidir, dins d’un grup de llimonades de les quals es coneix la proporció, quina és la que té més gust de llimona. A partir d’aquesta activitat inicial, la proposta de la qual és fer-la utilitzant aigua i suc de llimona, es van introduint activitats que han de permetre el treball amb diferents proporcions. Posteriorment, s’introdueixen altres barreges i diferents maneres de produir-les i, amb l’ús de diferents tipus de nombres, fraccions, decimals i percentatges, l’alumnat podrà decidir quina és la que tindrà més gust sense haver de tastar-la. Per acabar, s’introdueixen els preus de la llimonada com a elements d’ampliació de l’activitat.
A més a més del treball del bloc Model matemàtic, amb aquesta activitat l’alumnat treballa diferents sabers del sentit numèric i del sentit de la mesura. Per modelitzar la situació, s’haurà de dissenyar un experiment i així poder respondre les preguntes pertinents a través d’una bona organització de la informació obtinguda, per acabar prenent les decisions oportunes.
El món de les receptes, tot i que pot estar molt vist per l’estudiantat, pot ser un bon context per iniciar-se en la modelització matemàtica i que aquest reconegui les etapes del procés. Vegem-ne un exemple senzill. Es mostra a l’alumnat la següent imatge:

La proposta és la següent: Quins canvis hi haurà a la recepta de mousse de xocolata si l’hem de fer per a 6-9 persones? Fem una anàlisi de les diferents etapes del procés.
Es pot demanar a l’alumnat que presenti la recepta modificada per escrit, amb els supòsits ben definits i explicant detalladament com s’ha abordat la situació.
Amb la darrera proposta deixem els menjars i les begudes per donar pas als esports, un context de què també poden sorgir moltes situacions de proporcionalitat. Es tracta del problema de NRICH Triathlon and Fitness, que ens ofereix un context de la vida real per treballar proporcionalitat, velocitats i unitats de mesura. La resposta final pot sorprendre l’alumnat i el pot portar a preguntes interessants sobre la validesa del model proposat. Al web del problema podem trobar-hi diferents resolucions d’alumnes comentades.
Per plantejar l’activitat a l’aula es poden fer grups de 3 i lliurar una còpia de l’enunciat a cada grup. L’objectiu és esbrinar quin esportista ha cremat més calories en un triatló. L’enunciat és el següent:
El triatló és un esport que consta de tres curses consecutives: una de natació, una de bicicleta i, finalment, una cursa de córrer. Adam, Ben i Carles volen classificar-se per al triatló olímpic. Aquests són els seus resultats en una cursa de prova:
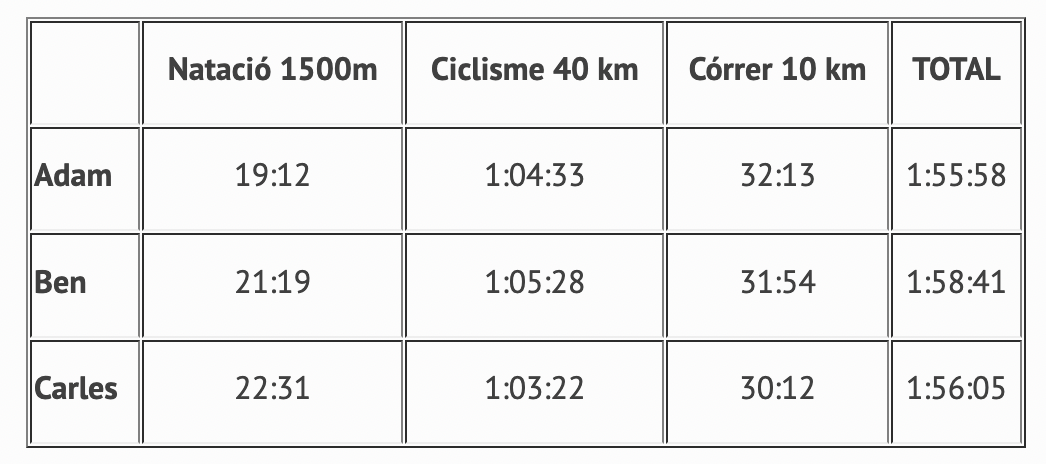
Quin esportista creus que ha cremat més calories?
Adam, Ben i Carles pesen aproximadament 70 kg cadascun. S’estima que els atletes d’aquest pes cremen energia als ritmes següents:
Suposant que la velocitat a la qual es cremen calories és directament proporcional a la velocitat dels atletes, calculeu quantes calories va cremar cadascun dels tres atletes durant la seva cursa. Us sorprèn? Com podeu explicar els vostres resultats? Creieu que els supòsits del model són vàlids?
Abans de fer cap càlcul, es demana que conjecturin quin esportista pensen que pot ser i que expliquin per escrit el perquè. Aquestes són algunes de les preguntes clau que es poden fer servir per ajudar els grups que es queden encallats: Què cal saber per calcular la velocitat de cada esportista? Com es pot calcular la velocitat en quilòmetres per hora? Si la seva velocitat (nedant) és inferior a (4,5) km/h, esperaries que cremés més o menys de 600 kcal per hora? Un cop sàpigues la velocitat a la qual crema calories, com calcularàs quantes calories crema en 19 minuts i 12 segons? Cap al final de l’activitat, es fa una posada en comú en què els diferents grups expliquen com han calculat el nombre de calories cremades en cada etapa del triatló. La resposta sorprèn gairebé sempre.
Cal recordar que el saber #1.ALG.MM.B és essencial, però que els recursos que s’acaben de descriure són només una proposta.
Apreciació de l’interès dels processos de modelització com a forma atractiva d’enllaçar les matemàtiques amb la realitat sobre la qual es vol actuar.
Ús de la proporcionalitat numèrica com a model matemàtic de situacions contextualitzades.
Anàlisi de les solucions d'un problema, presa de decisions en conseqüència i formulació de prediccions, si escau.
Llicenciat sota la Llicència Creative Commons Reconeixement CompartirIgual 4.0