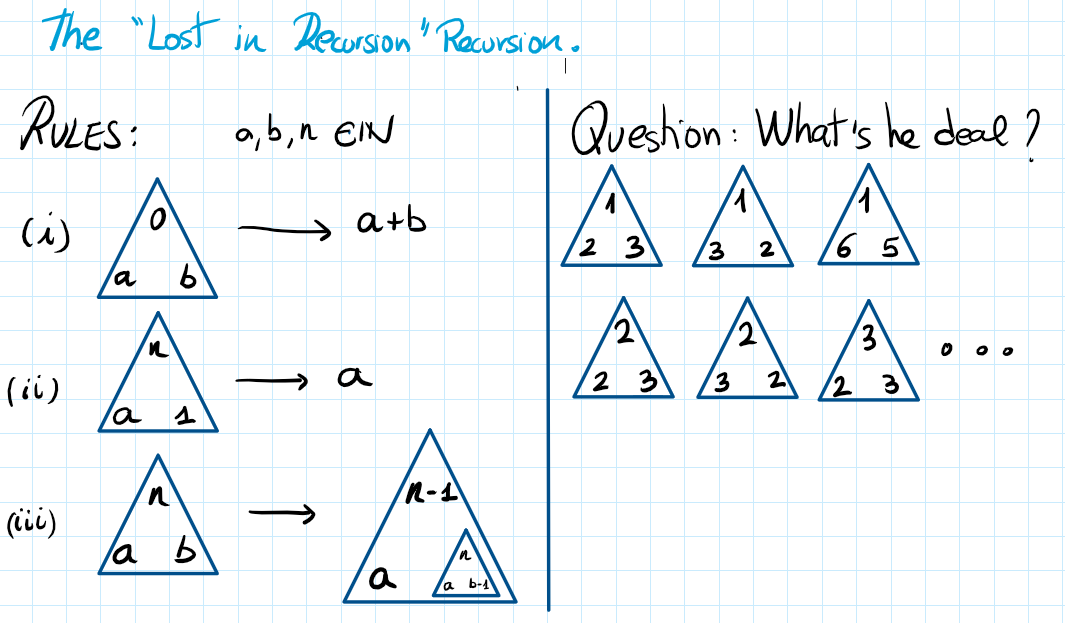Reflexions generals
El bloc dels sabers del pensament computacional es construeix de manera integrada dins de l’àmbit matemàtic i estableix connexions naturals amb altres sentits, especialment en el que ens trobem, l’algebraic, i amb el procés de resolució de problemes. Aquesta integració facilita la introducció i desenvolupament d’idees computacionals dins del treball matemàtic, com la descomposició, el reconeixement de patrons, l’abstracció i els algorismes (competència 4).
Els sabers s’han seqüenciat per oferir opcions diverses: des del pensament «desendollat» fins a la creació de programes en llenguatges tant visuals com textuals, i l’ús de dispositius mòbils o robòtica. Això permet adaptar l’ensenyament a les necessitats de cada curs i recurs disponible, per tal de mantenir sempre un enfocament pràctic i contextualitzat.
Observacions sobre alguns sabers d’aquest bloc
Una de les competències clau en el pensament computacional i vinculada a la resolució de problemes és el reconeixement de patrons, el saber #4.ALG.PC.A. Aquesta habilitat és fonamental per ajudar els alumnes a descompondre problemes complexos, generar hipòtesis, establir models matemàtics o detectar regularitats o similituds per millorar l’eficiència en la resolució de problemes. A més, aquest saber ha de permetre simplificar i generalitzar situacions, de manera que proporcioni una manera més eficaç d’organitzar la informació, i de predir futurs comportaments o resultats. El reconeixement de patrons involucra:
- Poder crear regles generals per aplicar a situacions anàlogues.
- Sistematitzar problemes aparentment complexos, identificant-hi regularitats.
- Fer prediccions d’un comportament futur d’un conjunt de dades estadístiques.
L’ús de grafs, la base del saber #4.ALG.PC.B, és una estratègia molt potent per a la resolució de problemes, ja que permet representar relacions complexes entre objectes o situacions de manera visual i estructurada. Com que, per desenvolupar-lo, es requereix un coneixement extra i no explícit al currículum, s’ha considerat un saber d’ampliació. Ara bé, les seves aplicacions al món real, facilitades per l’ús de principis bàsics i la representació visual, poden ajudar molt al desenvolupament del saber #4.ALG.PC.G, i aporten confiança i estímuls, contextualitzant i aproximant les matemàtiques a l’alumnat.
Amb el saber #4.ALG.PC.C, ens referim a aplicar estratègies pròpies de la informàtica, com la descomposició, el reconeixement de patrons, l’abstracció i la creació d’algoritmes, per abordar, entendre i resoldre situacions complexes de manera lògica i estructurada.
El vincle entre programació i la simulació d’experiments aleatoris que remarca el saber #4.ALG.PC.D permet a l’alumnat treballar conceptes de probabilitat intuïtivament i aprofundir en el món de la programació i el pensament algorísmic, que són habilitats fonamentals per al desenvolupament del pensament computacional. Aquest saber no es vol focalitzar només en continguts estocàstics, sinó en problemes que requereixin gran quantitat de càlculs per poder arribar a una solució satisfactòria.
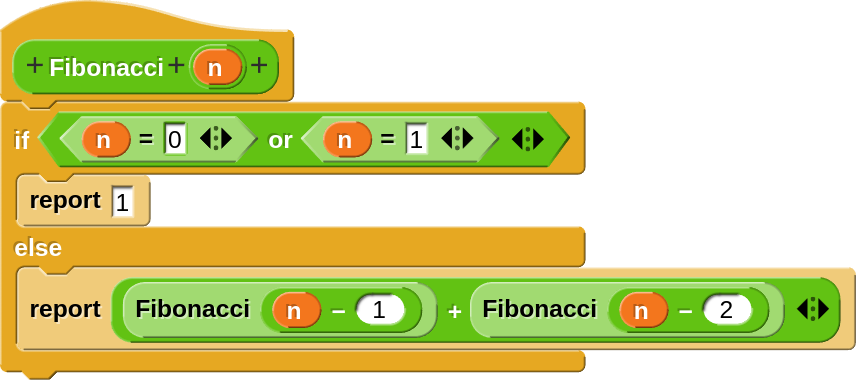
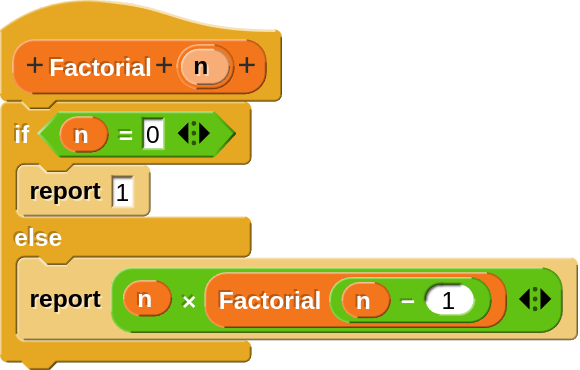
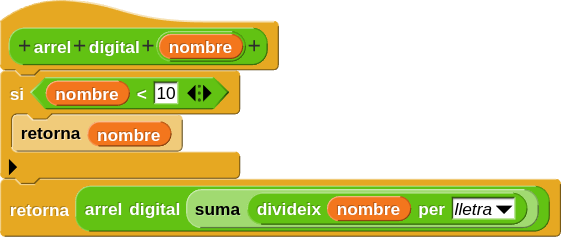
La idea de recursivitat que marca el saber #4.ALG.PC.E implica la definició d’una funció o procés que es refereix a si mateix per resoldre problemes de manera iterativa o repetitiva. És una eina que permet resoldre elegantment i eficaç certs tipus de problemes computacionals. També es pot vincular al concepte d’inducció matemàtica, fonamental per a la demostració de propietats matemàtiques. Com en el cas del saber #4.ALG.PC.B, i pel mateix motiu, s’ha considerat un saber d’ampliació.
El saber #4.ALG.PC.F involucra diferents dispositius digitals segons les necessitats:
- En el cas de les calculadores científiques es pensa tant en les funcions trigonomètriques, logarítmiques, exponencials, com en la funció factorial, nombres combinatoris, potència, arrel i conversió entre graus i radiants o el que disposi cada model. Tot per tal de trobar el valor directament i centrar-se en la interpretació del resultat, com en l’anàlisi de les propietats de les funcions.
- En els programes de geometria dinàmica, com GeoGebra o DESMOS, s’amplia el rang de funcions disponibles amb les pròpies del programa. L’ús permet focalitzar una anàlisi profunda de les propietats del problema geomètric, analític o estocàstic que es vol explorar.
- Els fulls de càlcul, com Excel, Google Sheets o LibreOffice Calc, permeten aplicar funcions matemàtiques per fer càlculs automàtics sobre grans quantitats de dades i combinar-les per generar-ne de noves.
- Finalment, els llenguatges de programació ofereixen la possibilitat d’implementar funcions matemàtiques per resoldre problemes algorísmics i simular processos matemàtics.
El pensament computacional no només tracta de desenvolupar competències tècniques, sinó també de potenciar habilitats personals i interpersonals necessàries per resoldre problemes complexos. Aquí entra en joc el saber #4.ALG.PC.G. Quan l’alumnat s’enfronti a problemes nous i desconeguts, la confiança en les capacitats d’un mateix els permetrà explorar solucions sense por del fracàs inicial. El fet de desenvolupar algoritmes, solucionar errors de codi o trobar patrons pot requerir molts intents; per tant, la persistència i la creativitat ajuden a superar obstacles i avançar cap a solucions eficients. En aquest context, sovint és necessari exercir l’adaptabilitat i la flexibilitat per reajustar els mitjans computacionals emprats als canvis en els requisits o a l’aparició de dificultats inesperades. Més enllà del pensament computacional les actituds esmentades són útils també en la resolució de problemes, en general, i es vinculen amb el sentit socioemocional, #SOE.