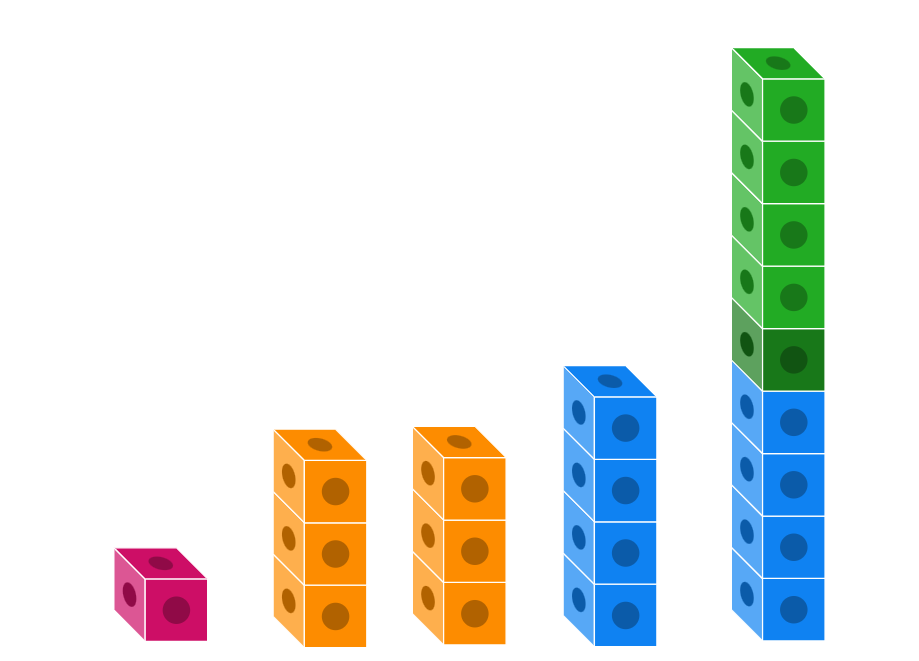Reflexions generals
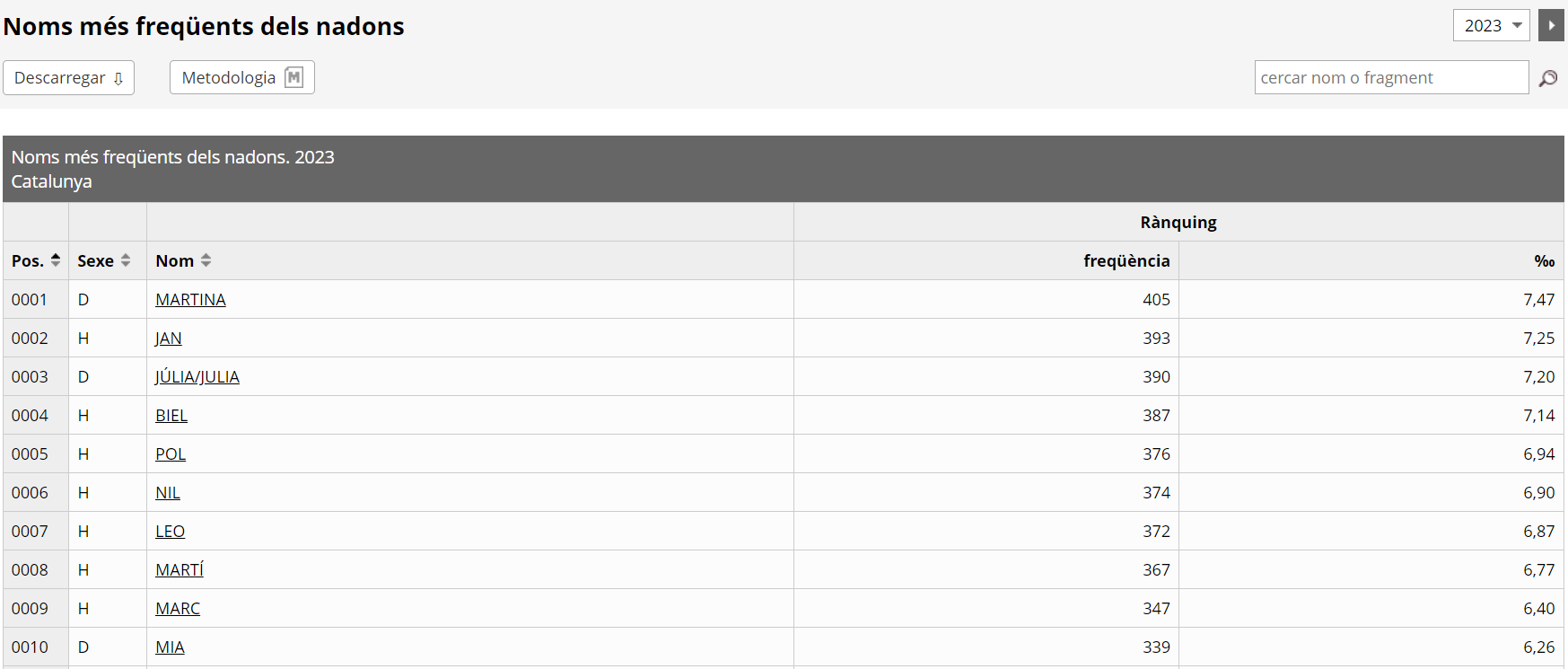
Per continuar el contacte amb els estudis estadístics ja realitzats a primària a 1r d’ESO, és recomanable treballar amb dades reals o dades recollides pel mateix alumnat, ja que aquestes dades proporcionen un primer acostament pràctic al procés d’investigació de l’estadística: elecció de mostres, redacció de preguntes, agrupaments de les dades, elaboració de taules de freqüències i redacció d’informes finals.
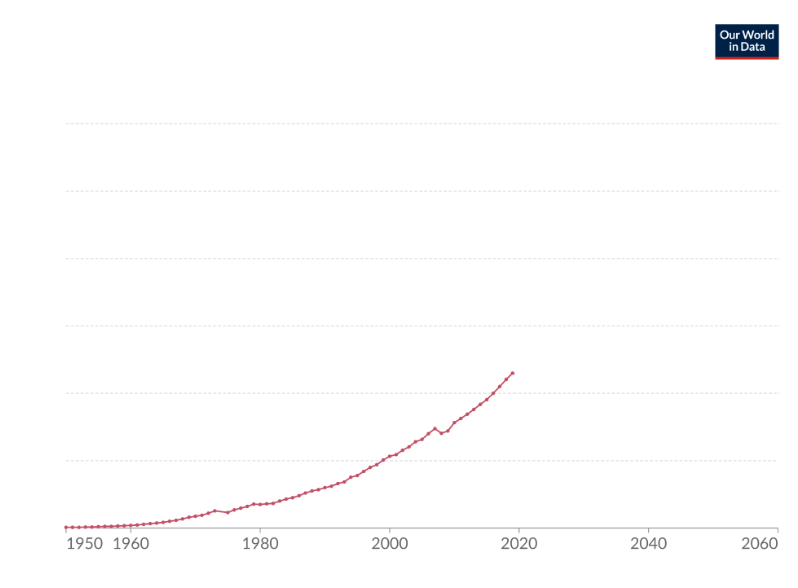
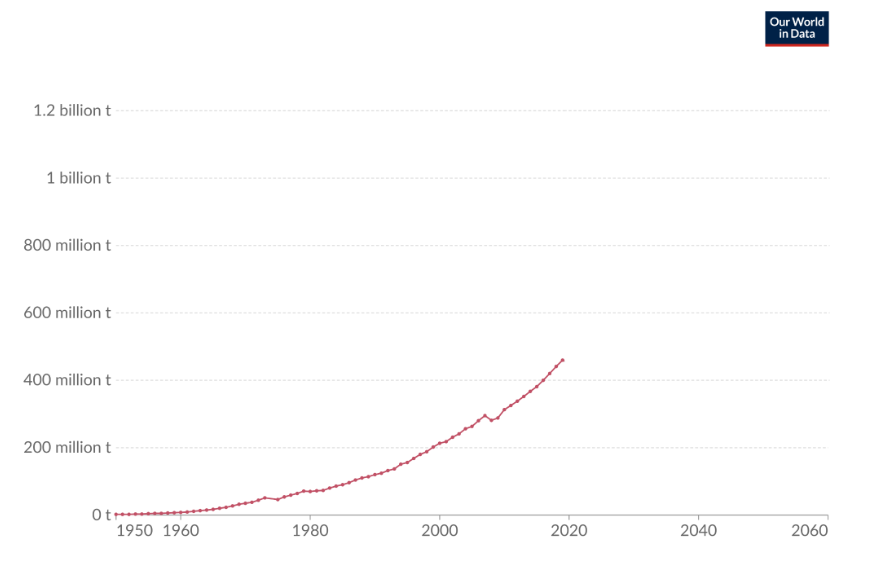
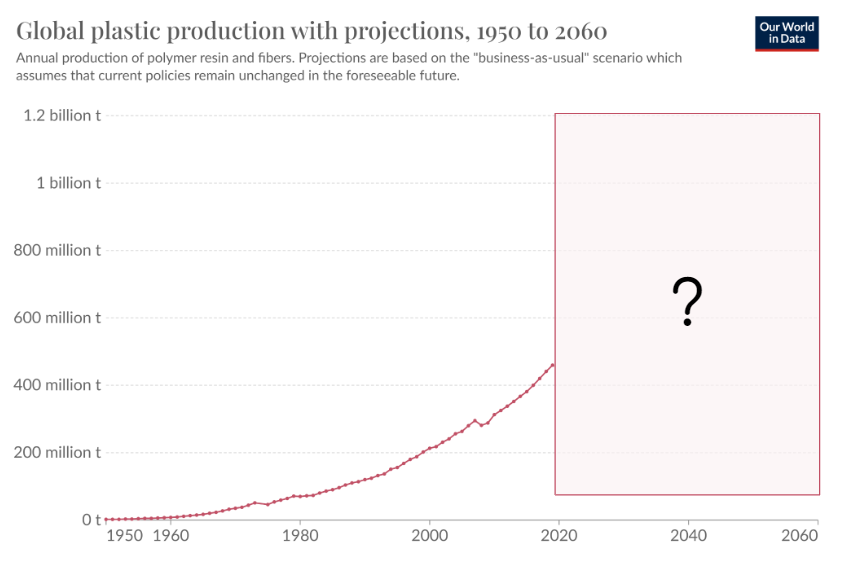
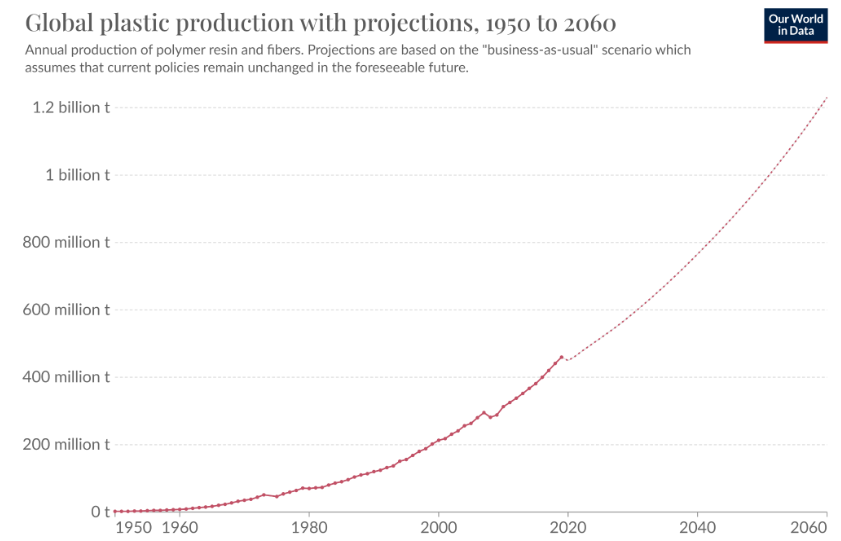
Per altra banda, el fet que l’alumnat acabarà convertint-se en consumidor crític dels resultats estadístics dels mitjans de comunicació, dona força importància al treball a l’aula per promoure les bones pràctiques d’anàlisis que s’han d’implementar com a rutines davant d’una informació representada en forma de gràfic: examinar sempre la font, l’escala i els eixos, el títol i el propòsit del gràfic, les unitats del gràfic o la llegenda.
És recomanable que a 1r d’ESO es facin els gràfics a mà, ja que aquesta pràctica permet treballar conceptes bàsics que no estan estrictament vinculats al sentit estocàstic, sinó que també reforcen altres blocs de contingut matemàtic. Per exemple, es fomenta l’aprenentatge de la creació d’eixos de coordenades, la divisió d’un segment en parts iguals, la subdivisió en intervals i l’ús d’eines com el regle i el transportador d’angles per elaborar gràfics de sectors. Deixem l’ús d’eines TIC per a la realització de gràfics per a 2n d’ESO, ja que és en aquest curs que es treballa més a fons l’ús i la programació dels fulls de càlcul, i s’ofereix així un context adequat per introduir aquestes eines de manera progressiva.
A l’hora d’elaborar gràfics: diagrames de barres, diagrames de sectors, histogrames, pictogrames, tija i fulles… és molt important que l’alumnat arribi a enunciar els criteris per seleccionar els que considera més pertinents per donar una bona representació de les dades que està treballant i aconseguir identificar algunes incorreccions que solen cometre’s en l’elaboració de les gràfiques, com per exemple errors en l’escala dels eixos de coordenades.
Les mesures de centralització com la moda, la mediana i la mitjana haurien d’orientar-se a reconèixer la necessitat d’aquest tipus de mesures i a comprendre’n les diferències. L’objectiu és que l’alumnat entengui en quin context és més adequat utilitzar cadascuna, més que no pas dedicar-se a fer càlculs reiterats. Aquesta comprensió és essencial per interpretar i justificar les decisions preses en l’anàlisi de dades.
Comentaris sobre les connexions
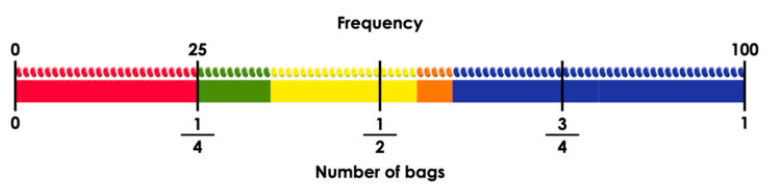
El bloc està relacionat de forma directa amb els sabers del sentit numèric a l’hora de treballar les taules de freqüències i els paràmetres estadístics, a l’hora de fer servir la fracció en contextos estadístics saber #1.NUM.QU.D. Per altra banda, l’ús de taules i representacions gràfiques en l’estudi i la modelització de situacions en contextos diferents contribueix a la comprensió del concepte de variable i, per tant, al saber #1.ALG.VA.D. Finalment, hi ha la connexió amb el sentit espacial saber #1.ESP.FG.F, encara que pot ser feble, la connexió existeix entre l’ús dels angles en un context no estrictament geomètric, com en els gràfics de sectors, i la comprensió de la proporció de les dades. En aquests gràfics, l’angle del sector representa visualment la proporció de les dades i connecta conceptes geomètrics amb el treball amb proporcions i interpretació de dades. Aquesta relació permet a l’alumnat veure com una eina matemàtica l’ús dels angles i com es poden aplicar en un context diferent, cosa que ajuda a consolidar-ne el significat i utilitat més enllà de la geometria.
Observacions sobre alguns sabers d’aquest bloc
Es considera essencial en aquest bloc de sabers el saber #1.EST.DI.A, tot i que, donada la seva importància, es treballarà durant tota la secundària. A 1r d’ESO aquest saber es considera essencial perquè els gràfics són la clau per a la interpretació i l’anàlisi de dades, i cal desenvolupar-lo des de les primeres etapes de l’educació secundària.
Altrament, es considera també essencial el treball al saber #1.EST.DI.B, ja que són conceptes fonamentals per fer qualsevol estudi estadístic.
Comentaris sobre els sabers essencials i d’ampliació
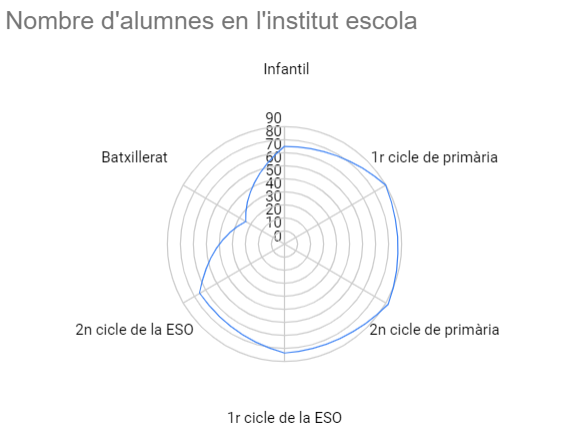
Pel que fa al saber #1.EST.DI.E, a 1r d’ESO caldria treballar la representació de dades en gràfics de tipologia diversa: gràfics de punts, línies poligonals, diagrama de barres, gràfics de tija i fulles i gràfics de sectors i polars… En l’elaboració de gràfics estadístics és fonamental la precisió, la claredat en els títols, l’elecció del tipus de gràfic i l’ús de les escales adequades. Si un d’aquests aspectes no es té en compte, el gràfic pot donar una idea inadequada de la informació que es pretén comunicar.
Identificació, representació i ús d’una fracció en diferents contextos.
Estudi de la circumferència i del cercle: centre, radi, diàmetre, longitud, el nombre pi, arc, corda i sector circular.
Variables estadístiques quantitatives i qualitatives.
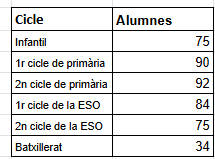
Anàlisi i interpretació de taules i gràfics estadístics simples (gràfics de punts, diagrames de barres, poligonals i sectorials).
Interpretació i reconeixement dels conceptes bàsics d’estadística: població i individu, mostra, variables estadístiques quantitatives i qualitatives discretes, freqüència absoluta i freqüència relativa.
Recollida i organització de dades quantitatives i qualitatives basades en observacions, dades públiques, enquestes, experiments i simulacions.
Confecció de taules de freqüències (absolutes i relatives) donat un conjunt de dades.
Representació inicialment manual d’un conjunt de dades donades a través de gràfics estadístics (gràfics de punts, de barres i de sectors, diagrames de tija i fulla…).
Comprensió, càlcul i interpretació de paràmetres estadístics de centralització (mitjana, mediana i moda) donat un conjunt de dades.