Blocs de competències: processos matemàtics i gestió socioemocional | Orientacions curriculars de matemàtiques de l’ESO

El conjunt de sabers que constitueix el sentit estocàstic, com tots els altres sentits, s’ha de relacionar amb el conjunt de competències del currículum. Sense un coneixement dels sabers, difícilment es poden desenvolupar els processos per avançar en l’assoliment de les competències i, d’altra banda, la manera com s’introdueixen, es construeixen i s’utilitzen els sabers és clau per fer un treball competencial.

Així doncs, tots els sabers poden contribuir a desenvolupar qualsevol competència si es treballen en activitats adequades. Igualment, un saber pot contribuir a desenvolupar diverses competències.

Es presenta la relació entre els sentits i les competències específiques a través dels processos: Resolució de problemes (competències específiques CE 1 i CE 2), Raonament i prova (competències específiques CE 3 i CE 4), Connexions, en què distingim les internes (competència específica CE 5) i les externes (competència específica CE 6), Comunicació i representació (competència específica CE 7) i Gestió socioemocional (competències específiques CE 8 i CE 9).

Aquesta relació, pel que fa al sentit estocàstic, es concreta, en el marc d’aquest exemple, de la manera que es descriu en els apartats següents, tot i que hi pot haver altres anàlisis igualment vàlides.

Resolució de problemes (CE 1 i CE 2)

L’estructura del treball estadístic, considerada de manera global, és idèntica a la del procés de resolució de problemes i, per què no, també a la del treball científic: formular preguntes, recollir dades, analitzar-les, interpretar els resultats i, finalment, respondre les preguntes plantejades.

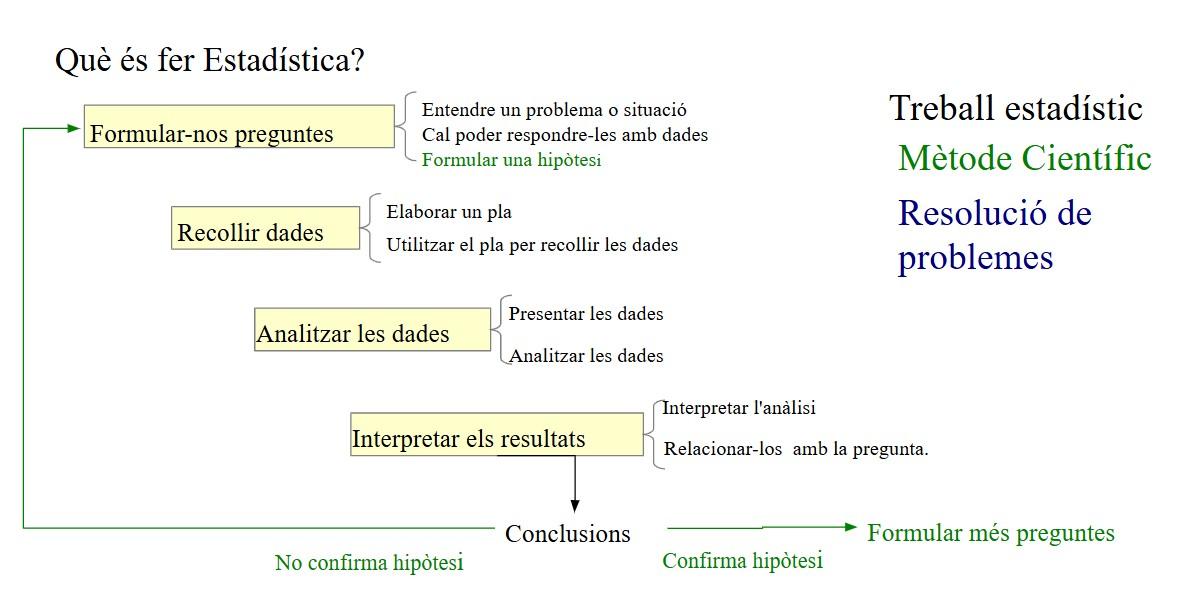
L’esquema de treball ens mostra que la part purament «matemàtica» de l’estadística (la reducció, l’anàlisi i la interpretació de les dades) és només una de les fases del procés, fins i tot la interpretació de les dades s’ha de fer sempre en funció del context del problema plantejat. En cursos anteriors ja s’ha treballat una de les parts més complicades de l’estudi estadístic: la fase de plantejament de preguntes, que és una de les més difícils i que, tot i que no es considera saber essencial a 4t, s’hi ha de posar èmfasi a l’hora del treball a l’aula.

Nolan i Speed (2002) proposen que el professor no hauria de centrar-se exclusivament en l’ensenyament de la terminologia estadística, sinó que hauria d’orientar l’aprenentatge cap a l’adquisició d’estratègies generals que puguin ser aplicades a diferents tipus de dades i contextos. Aquesta perspectiva posa èmfasi a desenvolupar en l’alumnat una comprensió pràctica i transversal de l’estadística, cosa que els permet abordar problemes reals i transferir els coneixements adquirits a situacions diverses, més enllà de l’aula. L’objectiu és formar pensadors crítics capaços d’utilitzar el raonament estadístic per interpretar, analitzar i actuar en una varietat de contextos.

De la mateixa manera cal saber aplicar els sabers relacionats amb la probabilitat per entendre situacions contextualitzades en què intervé l’atzar i ser conscients de les implicacions que això comporta. Per això és necessari dissenyar i implementar experiments per estudiar el comportament de fenòmens aleatoris que ens serveixen de model per a la interpretació, anàlisi i resolució i que ens permetin prendre decisions de forma fonamentada en la vida quotidiana.

Sabers

Alguns sabers d’aquest sentit fan referència directa al procés de resolució de problemes. Per exemple:

Anàlisi i interpretació de taules i gràfics estadístics de distribucions estadístiques unidimensionals o bidimensionals amb variables qualitatives, quantitatives discretes i quantitatives contínues, és a dir el saber #4.EST.DI.A, que es relaciona intrínsecament amb la CE 1.
El saber #4.EST.DI.C, representació de distribucions bidimensionals mitjançant núvols de punts. Recta de regressió, concepte i interpretació. Coeficient de correlació lineal: concepte i utilitat com a eina d’anàlisi, ens permet obtenir solucions matemàtiques mobilitzant els coneixements necessaris i discriminant l’existència de les diverses solucions a l’hora d’ajustar la recta de regressió i, per tant, aquest saber desenvolupa la CE1.
El càlcul i la interpretació dels paràmetres de centralització i de dispersió, saber #4.EST.DI.F, ja que proporcionen informació clau sobre com es distribueixen les dades al voltant d’un valor central i com estan de disperses. Aquest coneixement és essencial per a l’anàlisi i la interpretació de les dades i, per tant, desenvolupa la CE 2.
El saber #4.EST.IN.A, disseny d’investigacions i enquestes per donar resposta a una pregunta, repte científic o situació quotidiana que és essencial tant en el desenvolupament de la CE 1 com CE 2.
La Interpretació dels paràmetres de la regressió lineal i prediccions, saber #4.EST.IN.C, perquè la interpretació dels paràmetres d’una regressió lineal i les prediccions són passos essencials per abordar problemes de manera estructurada i informada. Mobilitzar els coneixements necessaris implica combinar tècniques estadístiques amb una comprensió profunda del problema per arribar a solucions efectives i, per tant, fomenta el treball de la CE 1.
El saber #4.EST.IN.D, interpretació dels paràmetres de les diferents funcions de regressió no lineal a través de programes informàtics i prediccions, escollir la funció de regressió com a model adequat segons la natura de les dades també connecta amb la CE 1.
El saber #4.EST.PI.C, el càlcul de probabilitats en casos donats utilitzant combinatòria que ens permet resoldre situacions en què intervé l’atzar per desenvolupar la CE 1.
El saber #4.EST.PI.D, centrat en la utilització de nombres aleatoris en càlculs de probabilitats a través de les simulacions, que connecta amb la CE 1.
El saber #EST.PI.E, aplicació del càlcul de probabilitats per prendre decisions fonamentades en diferents contextos que connecta amb la CE 2.

Recursos

Molts dels recursos esmentats per treballar diferents sabers fan referència directa al procés de resolució de problemes. Per exemple:

L’anàlisi de gràfics del web del Ministeri Escenarios climáticos del cambio climático:incertidumbre y certezas, esmentat al saber #4.EST.DI.A, implica extreure informació i entendre les tendències, les conclusions de l’anàlisi i la modelització; s’han d’entendre a proposta d’accions concretes i connecten el coneixement científic amb decisions quotidianes i sostenibles.
L’activitat Devising a Measure: Correlation de Mathematics Assessment Project tractada al saber #4.EST.DI.C, en què l’alumnat ha de proposar estratègies diverses i obtenir solucions a la recta de regressió, valorant la idoneïtat de les diverses propostes de l’alumnat de la classe.
L’activitat Enquesta electoral, proposada per Martí Casadell al saber #4.EST.IN.A, com una activitat completa des de la definició del problema fins a l’anàlisi de dades i la interpretació dels resultats.
L’activitat estadística i mobilitat del grup de Vilatzara, un recurs per treballar el saber #4.EST.IN.C que fa servir la recta de regressió per fer inferències estadístiques i predir quan i quants vehicles hi haurà a Castellar quan la seva població assoleixi els 30.000 habitants.
El recurs per treballar el saber #4.EST.IN.C del grup Vilatzara És rendible la publicitat?, que analitza quines haurien de ser les inversions d’una empresa en publicitat.
El recurs Càlcul de probabilitats en què es resolen diferents situacions que, en general, ens permeten treballar tots els sabers del bloc #4.EST.PI.
L’ús del Mètode de Montecarlo i la resta d’activitats en què es generen simulacions per treballar el saber #4.EST.PI.D.

Raonament i prova (CE 3 i CE 4)

L’estocàstica té un paper clau en el desenvolupament de competències de raonament i prova, així com en l’adquisició de sabers específics relacionats amb l’anàlisi i la interpretació de dades. A través de l’estudi de patrons d’incertesa i variabilitat, l’estocàstica permet explorar problemes reals amb una perspectiva crítica i fonamentada, i afavoreix la capacitat de prendre decisions informades i de comunicar resultats de manera efectiva.

En particular, l’estocàstica és essencial per treballar comparacions de distribucions de dades, analitzant mesures de posició i de dispersió que ofereixen una visió profunda sobre la variabilitat i la centralitat de les dades. Això permet identificar similituds i diferències entre conjuntures diverses, una habilitat indispensable en camps com la ciència, l’economia i la presa de decisions quotidianes.

Un altre aspecte central és l’anàlisi de la relació entre dues variables, que inclou conceptes com causalitat, correlació i regressió. Aquestes eines permeten discernir si hi ha una connexió entre variables i fins a quin punt l’una pot predir el comportament de l’altra, així com reconèixer possibles confusions entre associació i causa. Això no només enriqueix la comprensió teòrica, sinó que també ens ajuda a desenvolupar models per resoldre problemes complexos.

Finalment, l’estocàstica destaca per la seva aplicació pràctica en el context de l’anàlisi de resultats. La capacitat d’interpretar les dades i traduir-ne els resultats en recomanacions útils o implicacions per a un context específic és crucial. Aquesta competència combina habilitats de raonament matemàtic, anàlisi crítica i comunicació, i contribueix a desenvolupar una mirada reflexiva i rigorosa davant problemes reals, ja sigui a l’aula o en la vida quotidiana.

Sabers

Alguns sabers d’aquest sentit fan referència directa al procés de raonament i prova. Per exemple:

El saber #4.EST.DI.G, comparació de distribucions de dades atenent a mesures de posició i dispersió, que permet reconèixer tendències en els problemes i, per tant, connecta amb la CE 4.
Anàlisi de la relació entre dues variables, causalitat, correlació i regressió, saber #4.EST.IN.E, perquè desenvolupa la CE 4, reconeixement patrons, de similituds i de tendències.
El saber #4.EST.IN.F, anàlisi dels resultats per proposar i comunicar recomanacions pràctiques o implicacions dintre del context d’estudi, també vinculada a la CE 4, donat que valora el significat de les dades i permet reflexionar sobre els límits de l’anàlisi i de considerar possibles biaixos o errors en la interpretació.
El saber #4.EST.PI.A implica el disseny i la implementació d’experiments simples i compostos per estudiar el comportament de fenòmens aleatoris vinculat a la CE 3.
El saber #4.EST.PI.D, que lliga amb l’ús del pensament computacional per a la creació de simulacions que connecten directament amb la CE 4.
El saber #4.EST.PI.E, que rau en l’aplicació del càlcul de probabilitats per prendre decisions fonamentades en diferents contextos que lliga amb la CE 3.

Recursos

Molts dels recursos esmentats per treballar diferents sabers fan referència directa al procés de raonament i prova. Per exemple:

L’activitat Data Matching que es proposa a NRICH és un bon recurs per treballar el saber #4.EST.DI.G, atès que permet treballar el reconeixement de tendència, patrons i similitud de dades.
La pràctica de Sarah Carter de Boxplot and Histogram Card Sort Activity, també esmentada al saber #4.EST.DI.G, permet trobar els principis dels patrons de les dades, descartar les dades irrellevants del gràfic i identificar quines són les dades importants del conjunt.
La proposta Diagrames de dispersió del grup Vilatzara, esmentada al saber #4.EST.IN.E, permet construir i expressar argumentacions per justificar la relació que es creu que hi ha entre diferents variables estadístiques.
La grandària de les geleres, publicada pel grup Vilatzara, tracta el retrocés de les glaceres del cim del Kilimanjaro i el cas de l’Aneto i es treballa el saber #4.EST.IN.F.
Generalització de probabilitats, del blog Median, que, a través del raonament, ens permet arribar a generalitzacions de les situacions plantejades, lligat amb el saber #4.EST.PI.B.
Les tres vespes, de la Caixa de Varga, que, a través d’una simulació, permet arribar a una aproximació de la solució i es treballa el saber #4.EST.PI.D.

Connexions amb altres parts de la matemàtica (CE 5)

L’Estocàstica estableix connexions amb altres àrees matemàtiques, especialment amb l’àlgebra i el concepte de variable. En aquest context, les variables adquireixen una naturalesa dinàmica i representen resultats incerts i subjectes a probabilitats. Això enriqueix el seu significat més enllà del marc tradicional de l’àlgebra i ofereix una visió més contextualitzada i versàtil.

A l’aula seria interessant treballar que l’alumnat no confongui les dependències estadístiques amb les dependències funcionals (o funcions). En el cas de les funcions, sabem que, atès el valor de la variable independent, podem determinar amb certesa el valor de la variable dependent. Això és possible gràcies a la informació proporcionada per la taula de valors, la representació gràfica, la fórmula matemàtica o el coneixement de la llei que relaciona ambdues magnituds de manera precisa. En canvi, amb les dependències estadístiques podem obtenir una aproximació o una idea del valor que podria prendre una variable a partir del coneixement de l’altra, però no podem determinar aquest valor amb exactitud. Això es deu al fet que el resultat pot estar influït per altres factors, com ara l’atzar o la variabilitat inherent a les dades, pròpies de molts dels procediments experimentals.

A més, aquestes connexions entre l’àlgebra i l’estocàstica s’amplien quan es treballa el saber propi del sentit algebraic en la cerca de funcions que modelitzen situacions que segueixin models lineals, quadràtics, exponencials o de proporcionalitat inversa. Això permet establir relacions entre variables a través de representacions gràfiques, equacions i patrons numèrics, i comprendre com aquestes funcions reflecteixen situacions del món real o teòric.

Aquestes connexions formen un entramat integrat que permet a l’alumnat abordar problemes des de múltiples perspectives, aplicant conceptes de manera transversal i significativa.

Sabers

Alguns sabers treballats en el sentit estocàstic estan molt presents en tota la matemàtica, esdevenen eixos de connexió interna i, per tant, són peces fonamentals en el desenvolupament de la competència CE 5:

Anàlisi i interpretació de taules i gràfics estadístics de distribucions estadístiques unidimensionals o bidimensionals amb variables qualitatives, quantitatives discretes i quantitatives contínues, saber #4.EST.DI.A, donat que el treball amb variables en estadística és una aplicació directa del concepte algebraic de variable, ampliat a contextos reals.
El saber #4.EST.DI.B, recollida i organització en taules de contingència de dades bidimensionals, a l’hora de la recollida de dades en experiments aleatoris.
El saber #4.EST.DI.D, identificació, representació i ajust de funcions de regressió no lineals (polinòmica, exponencial, logarítmica…), vinculat amb el saber #4.ALG.MM.C.e
Interpretació dels paràmetres de les diferents funcions de regressió no lineal a través de programes informàtics i prediccions, #4.EST.IN.D, vinculada amb el saber del model matemàtic, saber #4.ALG.MM.C cerca de la funció que modelitza una situació (contextualitzada o no) que segueixi un model lineal, quadràtic, exponencial, de proporcionalitat inversa.
El disseny i implementació d’experiments simples i compostos per estudiar el comportament de fenòmens aleatoris, així com les simulacions que connecten amb el saber #4.ALG.PC.C.
Càlcul de probabilitats en esdeveniments dependents i independents, compatibles i incompatibles que connecten amb el saber #4.MES.ME.G.
Càlcul de probabilitats en casos donats utilitzant tècniques de recompte i combinatòria saber #4.NUM.CO.A i saber #4.NUM.RE.C.
Utilització de nombres aleatoris en càlculs de probabilitats. Simulacions, saber #4.ALG.PC.D.

Recursos

Molts dels recursos esmentats per treballar diferents sabers aporten o utilitzen connexions internes. Per exemple:

L’activitat esmentada al blog de Sarah Carter the paragraph function, esmentada al #4.EST.IN.D, permet ajustar la corba a una funció racional i reconèixer els paràmetres d’ajust.
El joc del 6 del grup cúbic, esmentat a #4.EST.DI.D, permet el treball mitjançant eines digitals de l’ajust a la corba exponencial.
L’activitat de Daus i triangles, esmentada al #4.EST.PI.E, permet donar resposta a una situació geomètrica de creació aleatòria de triangles.

Connexions amb altres matèries i amb l’entorn (CE 6)

L’estocàstica i, en concret, tots els sabers d’inferència estan profundament connectats amb la competència de vincular i contextualitzar les matemàtiques amb altres àrees de coneixement. Aquesta connexió permet interrelacionar conceptes i procediments matemàtics amb elements d’altres disciplines, cosa que potencia la capacitat per resoldre problemes de manera integral i significativa.

Aquest enfocament transversal de la inferència matemàtica no només reforça el coneixement estadístic, sinó que també enriqueix la comprensió global de situacions complexes, integrant les matemàtiques com una eina essencial en la resolució de problemes multidisciplinaris i en la presa de decisions informades.

Sabers

A continuació, s’indiquen, a tall d’exemple, alguns d’aquests sabers:

El saber #4.EST.DI.A, el saber #4.EST.DI.C i el saber #4.EST.DI.D permeten connectar les matemàtiques amb nombroses àrees del coneixement: altres ciències, actualitat, tecnologia... i, per tant, implica la construcció de models matemàtics per estudiar fenòmens naturals i socials. Per tant, reforcen la CE 6.
Els sabers d’inferència són, en general, una pura connexió amb altres àrees de coneixement com el disseny d’investigacions, el saber #4.EST.IN.A, la interpretació dels paràmetres de la regressió lineal i prediccions, saber #4.EST.IN.C o la investigació de l’aportació de l’estadística al camp de les ciències socials al llarg de la història, saber #4.EST.IN.G.
El saber #4.EST.PI.A i el saber #4.EST.PI.E ens permeten la connexió amb activitats experimentals d’altres disciplines i de la vida quotidiana.
El saber #4.EST.PI.F ens permeten mantenir una posició crítica davant dels jocs d’atzar i les seves conseqüències.

Recursos

Molts dels recursos descrits per treballar diferents sabers del sentit estocàstic ofereixen oportunitats per fer connexions externes. Per exemple:

L’anàlisi de gràfics esmentat al saber #4.EST.DI.A, Escenarios climáticos del cambio climático:incertidumbre y certezas, permet treballar les connexions entre les activitats humanes i els canvis en el clima i, per tant, desenvolupa la CE 6.
L’activitat Radioactive dice-half life del blog de Joe Cossete, esmentada al saber #4.EST.DI.D, i amb connexions en la física i les cadenes de desintegració nuclear.
Al blog de Vilatzara, l’activitat anomenada Comparant fòssils, busca correlacions dades en un context d’àmbit paleontològic.
L’estudi dels gràfics de Du Bois tractats al saber #4.EST.IN.G, i les seves repercussions en tractar les problemàtiques socials, especialment en el context de la comunitat afroamericana als Estats Units després de la Guerra Civil.
Les activitats Quin cadenat és més segur? i Simplex Lock tractades al saber #4.EST.PI.C ens proposen analitzar el funcionament de diferents tipus de cadenats i panys i la seva relació amb la combinatòria.

Comunicació i representació (CE 7)

L’estocàstica i, concretament, l’estadística és una disciplina essencial dins del camp de les matemàtiques, no només pel seu poder analític i aplicabilitat en contextos pràctics, sinó també pel paper que té en el desenvolupament de diverses competències matemàtiques fonamentals. Aquesta relació es manifesta de manera particular en tres sabers clau: comunicar informació de manera organitzada, representar conceptes amb claredat i dialogar per debatre idees matemàtiques.

Cal destacar que a 4t de l’ESO hem de treballar que l’alumnat integri diferents formes de representació per fer explícits conceptes i resultats i que sigui capaç de trobar la relació entre la representació visual en forma de gràfics com histogrames, diagrames de dispersió o gràfics de línies per il·lustrar tendències i patrons, la connexió amb la representació algebraica, l’ús de fórmules i expressions per descriure conceptes com la correlació o la regressió i la representació verbal amb explicacions clares dels resultats, connectant els càlculs matemàtics amb el context del problema estudiat.

Sabers

Alguns sabers del sentit estocàstic poden contribuir de manera especial al desenvolupament de la competència CE 7. Per exemple:

El saber #4.EST.DI.C, representació de distribucions bidimensionals mitjançant núvols de punts. Recta de regressió. Concepte i interpretació. Coeficient de correlació lineal: concepte i utilitat com a eina d’anàlisi.
El disseny d’estudis estadístics i el fet de ser capaç de proposar millores en la recollida, la representació i l’anàlisi de les dades, saber #4.EST.IN.A.
L’ús de tècniques i eines digitals per presentar, analitzar i treure conclusions dels resultats d’un estudi estadístic, és a dir el saber #4.EST.IN.B.
El saber #4.EST.IN.F analitza els resultats per proposar i comunicar recomanacions pràctiques o implicacions dintre del context d’estudi.
L‘elaboració de l’informe estadístic, saber #4.EST.IN.I.
El saber #4.EST.PI.B en el càlcul de probabilitats en esdeveniments dependents i independents, compatibles i incompatibles.

Recursos

Molts dels recursos esmentats per treballar diferents sabers del sentit estocàstic fan referència al procés de comunicació i representació. Per exemple:

Devising a Measure: Correlation de Mathematics Assessment Project referenciada al saber #4.EST.DI.C és una activitat molt adient per treballar CE7 perquè treballa la representació gràfica i també permet dialogar entre iguals per justificar les diverses estratègies emprades per fer el càlcul de l’ajust a la recta.
La proposta Don Steward, en la qual es demana a un alumne que endreci per ordre de preferència les fruites, el color preferit, les assignatures, també tractada en el saber #4.EST.DI.C, que permet visualitzar la possible correlació entre els gustos de la classe.
Estadística i esports del grup Vilatzara esmentada al saber #4.EST.IN.B perquè treballa la importància de comunicar la informació de manera organitzada.
L’activitat del grup Vilatzara Estadística i política que apareix al saber #4.EST.IN.F permet debatre la legitimitat del procés de les eleccions de Florida de l’any 2000.
L’estudi i la revisió dels informes estadístics del Reto Barcelona Dades Obertes, que s’esmenta en el saber #4.EST.IN.I.
El Joc del 6 presentat al saber #4.EST.PI.A en què es representen el model discret de la situació per trobar les diferents previsions.

Gestió socioemocional (CE 8 i CE 9)

L’estadística, com a eina fonamental per analitzar i interpretar dades, està profundament connectada amb habilitats tècniques i socioemocionals. El procés d’investigació estadística suposa enfrontar-se sovint amb nous reptes o analitzar dades de situacions desconegudes, cosa que pot fer que s’hagin d’interpretar resultats que no són intuïtius o replantejar hipòtesis inicials. L’autoconfiança, bàsica per gestionar les pròpies emocions, es construeix a mesura que es resolen aquests reptes mitjançant eines estadístiques. La perseverança també tindrà un paper fonamental en un disseny estadístic, per exemple en detectar que una correlació esperada no es dona, i això propiciarà reflexionar sobre possibles millores en el disseny o en la metodologia, veient els errors com a oportunitats per créixer. L’anàlisi estadística sovint també requerirà iteració i ajustaments successius. Aquesta perseverança no només reforça la capacitat d’aprendre de manera autònoma, sinó també l’actitud positiva davant la complexitat.

La gestió socioemocional està vinculada a dues competències específiques:

CE 8, relacionada amb el desenvolupament d’habilitats personals com les creences, les actituds i les emocions envers les matemàtiques.
CE 9, centrada en el desenvolupament d’habilitats socials com el treball en equip i la presa de decisions.

A continuació, s’indiquen alguns aspectes que, treballats des del sentit estocàstic, poden contribuir al desenvolupament de les competències CE 8 i CE 9.

Alguns aspectes que poden contribuir al desenvolupament de la competència CE 8

El potencial històric de l’estadística pot ajudar els alumnes a entendre la seva rellevància en la vida quotidiana i en la societat; el saber d’investigació sobre l’aportació de l’estadística al camp de les ciències socials al llarg de la història, saber #4.EST.IN.G, està vinculat precisament amb CE8. L’anàlisi dels gràfics de Du Bois, que podeu trobar a Library of Congress de Washington, potencien la valoració del paper fonamental de les matemàtiques en els estudis històrics.
El saber #4.EST.IN.H tracta la reflexió sobre l’ús ètic de les dades estadístiques i la responsabilitat en la interpretació i la presentació de dades; l’activitat que apareix a la revista SUMA 71 La paradoxa de Simpson, posa de manifest la importància de considerar el context i treballar les creences i la manipulació de dades.
El saber #4.EST.PI.E tracta l’aplicació del càlcul de probabilitats per prendre decisions fonamentades en diferents contextos.
El saber #4.EST.PI.F està centrat en la utilització del sentit crític en la valoració dels riscos que comporten els jocs d’atzar.

Alguns aspectes que poden contribuir al desenvolupament de la competència CE 9

L’estocàstica, amb els seus reptes inherents i la necessitat d’interpretar dades complexes, ofereix una plataforma ideal per practicar competències de col·laboració. Treballar en equip per resoldre problemes estocàstics fomenta la generació conjunta d’estratègies, ajuda a equilibrar les necessitats personals i grupals i potencia el reconeixement i la valoració de les aportacions dels altres. Així, l’estocàstica no només enriqueix el pensament matemàtic, sinó que també contribueix a desenvolupar habilitats socials i emocionals essencials per al treball col·laboratiu. A continuació, es destaquen un conjunt d’activitats concretes en aquest àmbit:

L’activitat de Mathematics Assessment Project, esmentadaal saber #4.EST.DI.C, Devising a Measure: Correlation, de la Universitat de Califòrnia a Berkeley i el Shell Center de la Universitat de Nottingham, en què es desenvolupen les competències vinculades a la resolució de problemes amb un interessant procediment de treball en grup.
Les activitats basades en jocs per crear diagrames de dispersió de Sarah Carter, esmentades al saber #4.EST. DI.C, l’activitat del Hula-hoop Scatterplot Activity, en què l’alumnat es posa en forma de cursa de relleus, cerca de la correlació del temps que triguem a menjar regalèssies segons la seva llargada, Twizzlers Linear Regression Lab Activity, el nombre de salts que pot fer una pilota de tennis amb el temps, Bouncing Tennis Balls Linear Regression Lab o la relació entre la mida de la mà d’una persona i la quantitat de caramels que pot agafar, Starburst Scatterplot Activity ofereixen excel·lents oportunitats per fomentar el treball en equip i la col·laboració.
Les activitats Quina és la funció de Núria Serra, referenciades al saber #4.EST.IN.D, donat que les activitats de caràcter experimental són clau per fomentar la cooperació, la comunicació i el treball en equip. Aquestes activitats requereixen que l’alumnat col·labori per planificar, executar i analitzar resultats, i promou habilitats com l’escolta activa, la resolució de conflictes i la presa de decisions conjunta.
Les activitats de Fitxes de colors per combinatòria, Les tres vespes i Daus i triangles, en què el treball en equip és bàsic per arribar a la solució.