Sabers
- Ús de factors de conversió que permetin comparar unitats de volum i capacitat, adequades a cada situació.
[ESS]#NUM.RP
En aquest bloc només hem considerat un saber, on es comparen les unitats de volum i capacitat. L’aparició de situacions en què el context aporta informació rellevant a l’alumnat i, alhora, facilita la seva identificació amb el problema, permet que l’estudiant pugui fer-se una representació mental de diferents unitats de volum i capacitat que li possibilita, més tard, fer mesuraments, estimacions, comparacions, etc. En aquesta línia, recomanem oferir experiències de mesurament en què es treballin no només amb aquesta magnitud derivada, la capacitat, sinó que reculli aprenentatges assolits en cursos anteriors relacionats amb altres magnituds, per tal d’afavorir la construcció de coneixement.
En general, quan es concreten activitats que treballen el sentit de la mesura, és difícil que no hi hagi connexió amb el sentit espacial. Tots dos sentits acostumen a aparèixer simultàniament. A més a més, però, justament en el saber #3.MES.MA.A també trobarem una connexió amb el raonament proporcional, propi del sentit numèric. La resolució de problemes en diferents situacions i contextos en què aparegui la comparació d’unitats de volum i capacitat, ja sigui mitjançant taules de proporcionalitat o amb factors de conversió, facilitarà la connexió amb #NUM.RP.
El fet de considerar un únic saber dins aquest bloc del sentit de la mesura ens porta directament a proposar-lo com a essencial. Alhora, cal tenir present la seva connexió, ja esmentada anteriorment, amb el sentit numèric. Això permet dissenyar propostes relacionades amb aquest saber que afavoreixin un aprenentatge significatiu i ben connectat.
La comparació entre unitats de volum i capacitat, així com la seva adequació segons l’objecte i l’ordre de la magnitud mesurada, serà fonamental per ajudar l’alumnat a establir unitats patró de mesura. Aquestes unitats els permetran fer estimacions i mesuraments en situacions de resolució de problemes.
Ús de factors de conversió que permetin comparar unitats de volum i capacitat, adequades a cada situació.
A continuació, es presenten algunes idees sobre recursos i activitats d’aprenentatge que poden contribuir a l’adquisició dels sabers d’aquest bloc.
Per treballar el saber #3.MES.MA.A proposem activitats contextualitzades en què calgui comparar unitats de capacitat i volum. Sovint aquesta comparació no serà objecte d’estudi, sinó que formarà part del procés de la mateixa activitat. Si volem que les propostes siguin riques, el més habitual serà que, a part de tenir una forta connexió externa, amb continguts aliens a la matemàtica, es mobilitzin moltes de les competències específiques i es treballin també sabers referents al bloc de mesurament i al de l’estimació.
La capacitat total dels embassaments de les conques internes a Catalunya és d’uns 700 hm3. I en situació de normalitat, Catalunya consumeix 1 hm3 diari d’aigua.
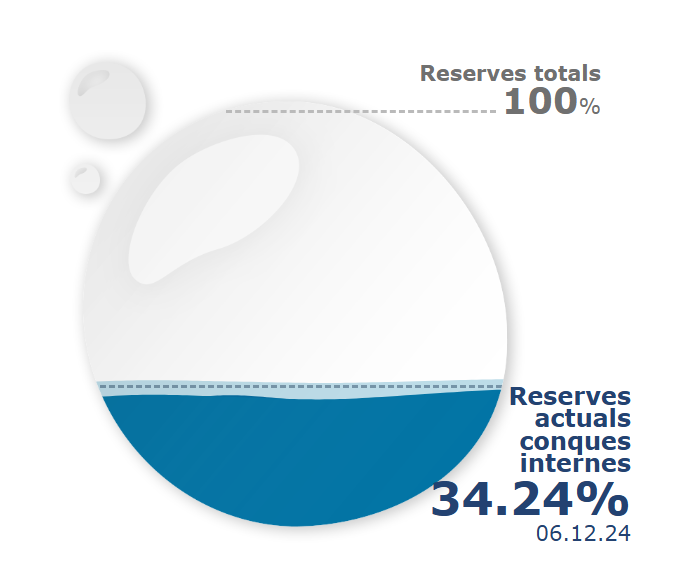
En la imatge anterior, obtinguda d’aquest portal de la Generalitat, tenim representat el percentatge de les reserves d’aigua en data 6 de desembre de 2024. Podem convidar l’alumnat que exposi quines preguntes els suggereix aquesta imatge. Amb la informació que tenim, es pot saber la quantitat d’aigua que hi ha en els embassaments? És molta, poca, suficient? Quina informació necessitem per poder decidir amb criteri la resposta a la pregunta anterior?
Des de les Dades Obertes de la Generalitat es pot accedir a la quantitat d’aigua als embassaments de les conques internes de Catalunya.
Es poden fer estudis de l’evolució de l’aigua als embassaments durant un any sencer, o fer comparacions fixant el dia i el mes, i observar-ne l’evolució modificant l’any, etc.
Ara bé, què vol dir que diàriament a Catalunya consumim 1 hm3 d’aigua? Podem imaginar-nos què és 1 hm3?
Per arribar a concebre aquesta quantitat necessitem oferir propostes d’experimentació a l’alumnat que l’ajudin a trobar una unitat patró que li permeti aquesta visualització.
Un exemple interessant el van proposar les professores Laura Morera i Cecilia Calvo en la Jornada d’Educació Matemàtica 2024 de l’associació APMCM, amb la seva conferència Mesures que deixen empremta: Trajectòries d’aprenentatge a l’educació obligatòria. Proposen una activitat de comparació en què, a partir de la conversa entre el grup classe, o en petits grups, caldrà decidir si un seguit d’afirmacions són certes o falses. No es tracta de calcular, sinó de raonar la veracitat d’aquestes sentències a partir de les referències que tenen els mateixos alumnes.
| La importància de les referències | ||
| Cert | Fals | |
| En un got hi caben 250 ml. | ||
| En una ampolla de 2 l hi caben uns 8 gots d’aigua. | ||
| 1 l equival a 10 ml. | ||
| En una banyera hi caben 2.000 l. | ||
| El mar Mediterrani conté més aigua que l’oceà Atlàntic. | ||
| En una piscina olímpica hi caben 2 milions i mig de litres. | ||
Font: Mesures que deixen empremta: Trajectòries d’aprenentatge a l’educació obligatòria
Autores: Laura Morera i Cecilia Calvo
Un cop completada la taula, es planteja la següent pregunta: quantes piscines olímpiques plenes d’aigua necessitem per tenir un hectòmetre cúbic?
Seguint amb l’estudi dels embassaments a Catalunya, cal destacar que el dia 8 de març de 2024 es va assolir un mínim històric de 100,09 hm³, equivalent al 14,41 % de la seva capacitat. D’acord amb aquesta dada, podem investigar a partir de quina quantitat es declara l’estat d’excepcionalitat, en quin punt s’activa l’estat d’alerta, quines restriccions de consum s’aproven i què representen aquestes quantitats en termes pràctics.
Sabem quantes piscines hi ha a Catalunya? Enmig d’una situació de sequera per manca de pluges, al febrer de l’any 2024 els diaris publicaven una notícia referent a la quantitat de piscines que hi havia al país. Per exemple, podeu consultar la notícia que publicava el diari La Vanguardia, el 18 de febrer de 2024, sota el títol El país de les 200.000 piscines.
Pot ser un exercici interessant considerar les mides d’una piscina mitjana, la seva capacitat, i el consum que representa omplir-les totes.
La connexió entre les matemàtiques i la societat en aquest cas es fa evident. Aprofitant un context actual i proper, com és el canvi climàtic i els períodes de sequera a Catalunya, podem treballar el sentit de la mesura i analitzar quines accions com a col·lectiu ens convenen per tal de cuidar el medi ambient.
Una observació de les capacitats d’algunes ampolles de begudes comercials o recipients que contenen líquid pot provocar certes preguntes sobre unitats, conversió entre aquestes, conveniència d’emprar múltiples i submúltiples en funció del context on es troben: llaunes de refresc de 237 ml, ampolles de vi de 750 ml, etc. En alguns casos trobarem una invitació a conèixer les unitats imperials, com ara el galó americà, i com els seus múltiples i submúltiples no són amb potències de 10, com passa amb les unitats del sistema mètric decimal, sinó amb potències de 2.
| 1 Galó | |||||||||||||||
| ½ Galó | ½ Galó | ||||||||||||||
| 1 Quart | 1 Quart | 1 Quart | 1 Quart | ||||||||||||
| 1 Pinta | 1 Pinta | 1 Pinta | 1 Pinta | 1 Pinta | 1 Pinta | 1 Pinta | 1 Pinta | ||||||||
| 1 tassa | 1 tassa | 1 tassa | 1 tassa | 1 tassa | 1 tassa | 1 tassa | 1 tassa | 1 tassa | 1 tassa | 1 tassa | 1 tassa | 1 tassa | 1 tassa | 1 tassa | 1 tassa |
| 2 gills | 2 gills | 2 gills | 2 gills | 2 gills | 2 gills | 2 gills | 2 gills | 2 gills | 2 gills | 2 gills | 2 gills | 2 gills | 2 gills | 2 gills | 2 gills |
| 8 oz | 8 oz | 8 oz | 8 oz | 8 oz | 8 oz | 8 oz | 8 oz | 8 oz | 8 oz | 8 oz | 8 oz | 8 oz | 8 oz | 8 oz | 8 oz |
Font: Mesures que deixen empremta: Trajectòries d’aprenentatge a l’educació obligatòria
Autores: Laura Morera i Cecilia Calvo
Hi ha molts exemples que connecten el sentit espacial i el de la mesura amb el nostre dia a dia, i amb objectes quotidians. Són una oportunitat idònia per treballar la mirada matemàtica del nostre alumnat i evidenciar-la en el quotidià. Tal com assenyala Alsina (2022, pàg. 61):
No deja de ser curioso que en el caso del vino se haya impuesto el tamaño de 75 cl. ¿Por qué no son de 1 litro? El origen parece provenir de Francia, donde se consideró (fíjate bien en lo que viene) que 75 cl era ideal para marcar una cantidad razonable que un solo obrero podía consumir durante el almuerzo para seguir trabajando por la tarde.
Alsina (2022, pàg. 61)
Llicenciat sota la Llicència Creative Commons Reconeixement CompartirIgual 4.0