Sabers
- Aplicació de les propietats geomètriques de figures planes i de tres dimensions en la resolució de problemes. Ús de la geometria dinàmica per a la recerca de la solució, si s’escau.
El bloc de formes geomètriques de dues i tres dimensions es treballa intensament a 1r i 2n d’ESO. A 4t d’ESO s’ha considerat posar un únic saber que, més que un saber generador de coneixement, pretén recollir els continguts ja treballats per aplicar-los en diferents situacions. Així doncs, per treballar aquest saber el que serà important és trobar les situacions adequades que requereixin l’ús de propietats ja conegudes, com podrien ser, per exemple, el teorema de Tales o el de Pitàgores.
El saber d’aquest bloc no ha estat connectat a cap altre bloc de continguts del currículum perquè no hi ha una connexió real amb un saber concret, sinó que seran les activitats que es proposin per treballar alguns sabers determinats, per exemple, del bloc de relacions i funcions del sentit algebraic, les que permetran generar aquesta connexió.
No s’ha marcat el saber d’aquest bloc com a essencial perquè s’ha considerat que, en el marc de 4t d’ESO, no és prou rellevant, malgrat que es consideri que les propietats geomètriques sí que són bàsiques per resoldre les diferents situacions que es puguin proposar.
A continuació, es presenten algunes idees sobre recursos i activitats d’aprenentatge que poden contribuir a l’adquisició dels sabers d’aquest bloc.
Per treballar el saber #4.ESP.FG.A hi ha el projecte «Crea el teu envàs» de Maite Gorriz i Santi Vilches. El projecte té com a objectiu crear un envàs. El treball comença amb l’exploració de l’experiència prèvia, que consisteix a definir amb les paraules pròpies de l’alumnat què és un cub, i fer la construcció amb vocabulari adient utilitzat de forma rigorosa.
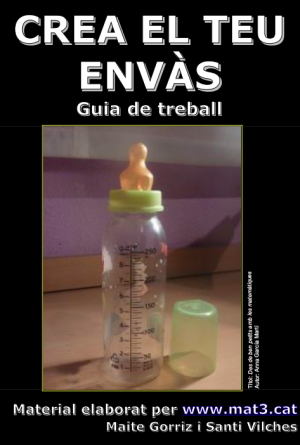
El que es pretén és modelitzar el càlcul de volums a partir de la comparació amb un patró que es correspon a una unitat de mesura concreta: la unitat cúbica. S’estudien diferents tipus de cossos geomètrics a partir d’envasos que porta l’alumnat per acabar dissenyant un nou envàs.
Tot i que la proposta inicial dels autors està formulada per a 2n d’ESO, com que un dels punts més forts d’aquest projecte és que és un problema obert i permet que l’alumnat sigui creatiu amb les seves propostes, es pot adaptar a diferents cursos i nivells. En funció de la seva proposta es pot estirar més o no, adaptant-nos a les capacitats i utilitzant tanta matemàtica com sigui necessària.
També per treballar el saber #4.ESP.FG.A, hi ha el recurs «Serpentine Lake» del web Underground Mathematics que, a més de la resolució de problemes a través de l’aplicació de les propietats de figures 2D i l’ús de programes de geometria dinàmica, comporta un treball de mesura important.
A la proposta, es presenta a l’alumnat una imatge d’un llac de Londres:
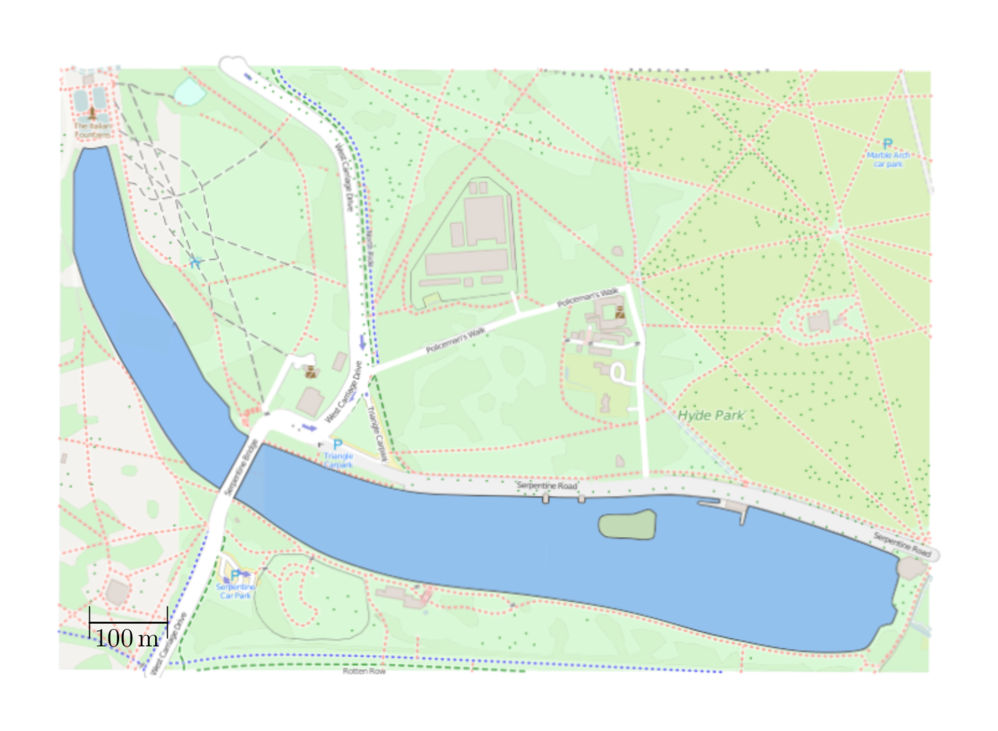
Tot seguit, se’ls explica que el llac té 40 hectàrees. Com ho poden comprovar?
En primer lloc, caldrà establir els límits del llac i després trobar estratègies de resolució. Es pot aproximar la forma del llac per trapezis, i acabar introduint la regla dels trapezis:
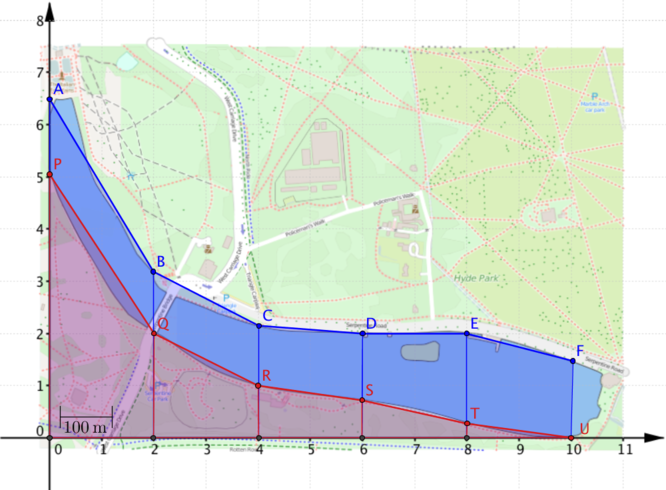
Algunes qüestions interessants que poden plantejar-se mentre l’alumnat està treballant són, per exemple:
Al llarg de 4t d’ESO, en molts contextos apareixerà la necessitat d’utilitzar eines apreses durant els cursos anteriors relacionades amb les formes geomètriques. Un d’aquests contextos pot ser el treball amb els nombres irracionals, lligat al saber #4.NUM.QU.B. Els nombres irracionals apareixen de manera natural quan treballem amb figures geomètriques cercant longituds, superfícies o volums desconeguts. Això ens proporciona un context perfecte per treballar les formes geomètriques, ara ja utilitzant els nombres exactes i no les seves aproximacions decimals.
A l’entrada del PuntMat «Nombres irracionals i materials manipulatius» es poden veure moltes propostes per treballar els nombres irracionals a partir de les figures geomètriques que trobem en el tangram clàssic, els pattern blocks o treballant amb geoplans.
Una altra activitat interessant per treballar-ho, que podríem titular «Quadrat de Puig Adam», és la que expliquen Alsina, Aubanell i Burgués en la seva obra Tres professors de matemàtiques (2019, pàg. 100), extreta del llibre Didáctica matemática heurística (Puig Adam, 1956) i que forma part del capítol que es titula «Iniciación al cálculo con irracionales cuadráticos».
Es tracta de repartir un grapat de peces de dos tipus: triangles rectangles isòsceles el catet dels quals mesura una unitat i rombes que tenen de costat la unitat i un angle agut de 45°. Després de familiaritzar-se amb les peces, es pregunta pels valors dels perímetres, els seus angles interiors i les seves àrees. Es pot veure que la del triangle val ½ i la del rombe, \(\frac{\sqrt{2}}2\). Es pot demanar també construir petits mosaics amb les figures. Arribats en aquest punt, es pot entrar de ple en el treball de raonament a partir de preguntes com: «Seria possible construir una figura formada tan sols per triangles que tingués la mateixa àrea que una figura formada tan sols per rombes?». La intenció de la pregunta és clara: fer adonar l’alumnat d’aquesta impossibilitat a partir dels càlculs fets anteriorment, donat que \(\sqrt{2}\) és incommensurable. Si anem més enllà, podem deduir que l’àrea de tota figura composta per aquests triangles i rombes tindrà una part racional procedent dels triangles i una part irracional procedent dels rombes. Això permet resoldre el problema-repte següent:
Sabent que el mosaic que hi ha a sota és quadrat i conté només els dos tipus de peces anteriors, i veient només aquesta petita part del mosaic, podríem deduir quants triangles i quants rombes el componen?


Sembla que no disposem de prou informació, però en realitat és possible respondre la pregunta. La resolució passa per la diferenciació de la part d’àrea racional i la part d’àrea irracional del mosaic. Tenint en compte la mida del costat, podem saber l’àrea del mosaic quadrat i, a partir d’aquí, diferenciar les parts racional i irracional, amb la qual cosa sabrem el nombre de peces de cada tipus fent un parell de divisions.
Les peces es poden imprimir en paper i plastificar o bé podem descarregar el disseny per a impressió 3D creat pel CREAMAT.
I ja per acabar, anomenarem la prova Cangur, que pot ser una font inesgotable de recursos i idees per treballar aquest saber. Podem trobar-hi propostes com les que es mostren a les imatges següents:


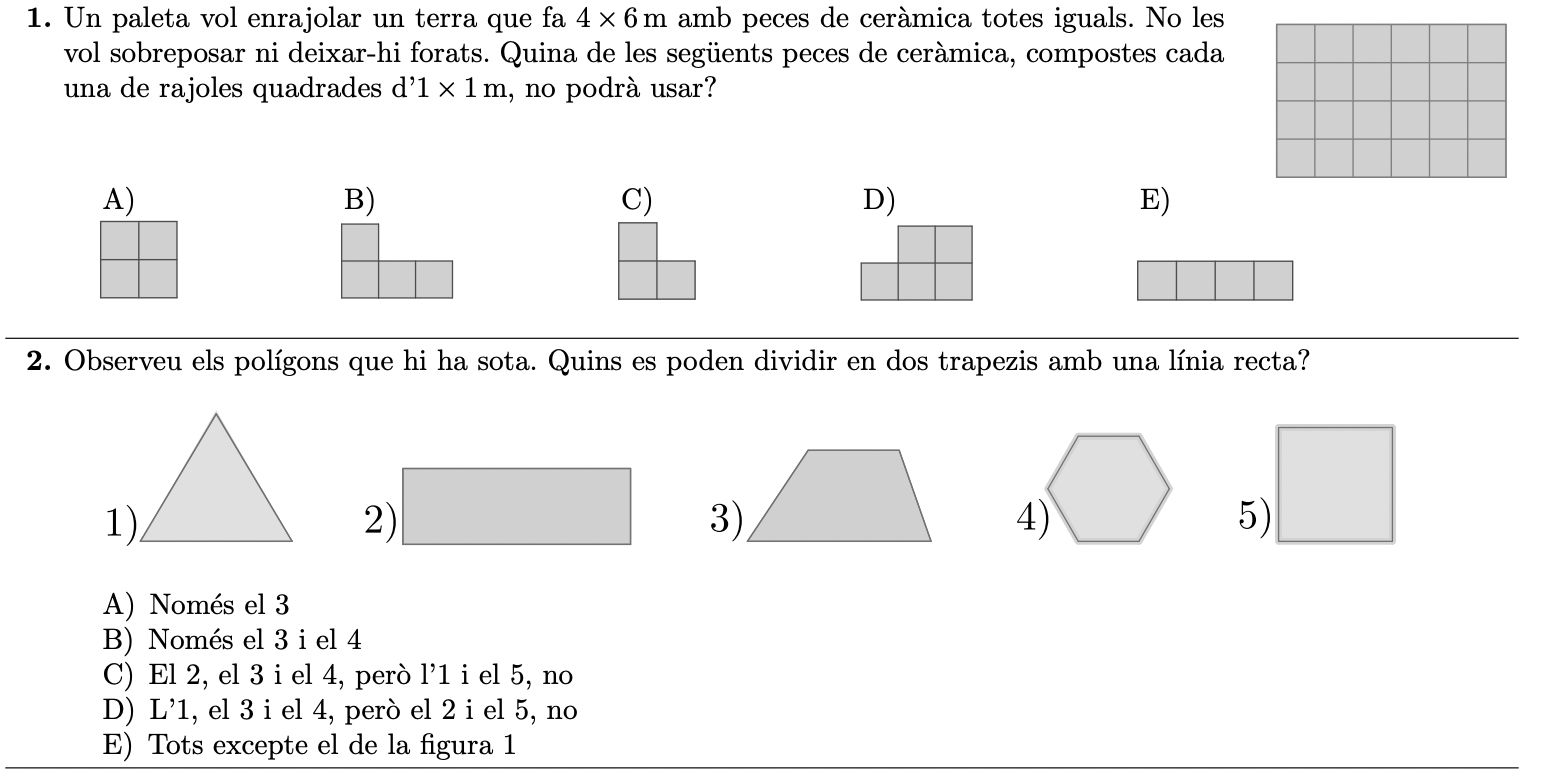
Llicenciat sota la Llicència Creative Commons Reconeixement CompartirIgual 4.0