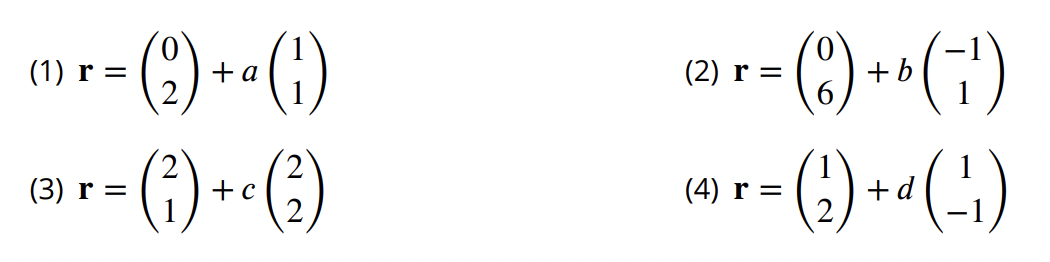Localització i sistemes de representació

Sabers

Comprensió del concepte i característiques (mòdul, direcció i sentit) dels vectors com a desplaçament entre dos punts.
[ESS]
Càlcul de les components d’un vector. Determinació del mòdul d’un vector a partir de les components.
Ús dels vectors, les seves propietats i les operacions entre ells per resoldre problemes geomètrics senzills.
[ESS]
Estudi de les diferents equacions d’una recta.
[AMP]

#ALG.ID

#ALG.RF
Determinació dels elements determinants d’una recta (punts, vector director, pendent, angle respecte a l’eix d’abscisses…) donada la seva equació.
[AMP]
Estudi de la posició relativa de dues rectes i determinació del paral·lelisme, la perpendicularitat i el punt de tall, si escau.
[AMP]

#ALG.ID

#ALG.RF
Selecció de l’equació de la recta més adequada en funció de la situació a resoldre.
[AMP]

Descripció i orientacions

Reflexions inicials

El bloc Localització i sistemes de representació entra amb força a l’últim curs d’ESO. A 2n d’ESO, abans de començar l’estudi de funcions, ja s’ha treballat la localització de punts en el pla; la idea de vector també ha aparegut a 3r d’ESO dins el marc de les translacions i l’alumnat també ha treballat amb les rectes i, fins i tot, amb algunes de les seves expressions en el moment de treballar sistemes d’equacions i funcions lineals o afins, però no és fins a 4t d’ESO que s’introdueix la geometria analítica i es treballen els conceptes de vectors i rectes de forma explícita.

Els sabers d’aquest bloc tenen dues característiques que, a priori, poden semblar contradictòries. Per una banda, la importància de les magnituds vectorials o la modelització de situacions mitjançant equacions lineals (de dues incògnites) genera la necessitat de treballar tots els sabers d’aquest bloc de la manera més rigorosa i profunda possible. Per altra banda, el treball entorn d’aquests sabers requereix un nivell d’abstracció important i cal tenir present que, malgrat que sigui l’últim, el 4t d’ESO encara és un curs d’educació obligatòria que, en principi, cursen tots els alumnes. Saber trobar l’equilibri entre aquestes dues realitats serà molt important per prendre les decisions corresponents adaptades a la realitat de cada aula. Visualitzar i manipular tot el que sigui possible pot ajudar a rebaixar el grau d’abstracció necessària i que un nombre més elevat d’alumnes sigui capaç d’entendre els conceptes que s’hi treballen.

Comentaris sobre les connexions

Els sabers d’aquest bloc que tracten sobre rectes bloc estan estretament vinculats amb el sentit algebraic. Per una banda, amb el bloc Igualtat i desigualtat ( #ALG.ID), en què cal entendre per què es parla d’equació de la recta i on es tracta la classificació de sistemes i, per altra banda, amb el bloc relacions i funcions ( #ALG.RF), en què hi ha una vinculació molt estreta entre l’estudi de la funció afí i els seus paràmetres i l’equació explícita de la recta.

Comentaris sobre els sabers essencials i d’ampliació

Aquest bloc està dividit en dues parts molt diferenciades, una de sabers entorn dels vectors i l’altra de sabers entorn de les rectes. S’ha decidit que els sabers essencials fossin de la part de vectors perquè aquests sabers alimenten el treball que es fa en altres assignatures i perquè recull i tanca un treball iniciat a tercer amb la introducció del concepte. Dins els sabers que tracten els vectors, s’ha considerat essencial la comprensió del concepte (saber #4.ESP.LS.A) i l’aplicació en problemes senzills (saber #4.ESP.LS.C), perquè es considera que els càlculs necessaris (saber #4.ESP.LS.B) no quedaran sense treballar. Per altra banda, s’ha trobat oportú considerar d’ampliació els sabers que tracten les rectes amb la idea de, si és necessari, reduir-ne l’aprofundiment o l’abstracció. Malgrat aquesta etiqueta, es vol animar, sempre que sigui possible, a treballar també aquest grup de sabers. Cal tenir en compte que moltes idees relacionades amb les rectes ja s’han treballat des d’altres sentits, fins i tot, en cursos anteriors.

Recursos i activitats

Recursos i activitats generals per al bloc de sabers

Per treballar els sabers de tot el bloc, inclosos els d’ampliació, hi ha el recurs a l’ARC «Vectors i rectes en el pla», de Victòria Oliu. La seqüència d’activitats consta d’un joc de rol per convertir l’alumnat en punts del pla amb les seves coordenades i representar així rectes «vivents» a partir de l’equació. També s’hi troben activitats de GeoGebra interactives per repassar conceptes bàsics de geometria plana, introduir els nous conceptes i plantejar reflexions. Inclou, així mateix, fulls de treball per copiar els enunciats canviant les dades i fer problemes a classe, intercanviant els enunciats per parelles. I, per acabar, s’hi troben les activitats finals: l’elaboració d’un mapa conceptual de tot el que s’ha treballat i la proposta d’invenció d’un problema per intercanviar.

Recursos i activitats per treballar sabers concrets

A continuació, es presenten algunes idees sobre recursos i activitats d’aprenentatge que poden contribuir a l’adquisició dels sabers d’aquest bloc.

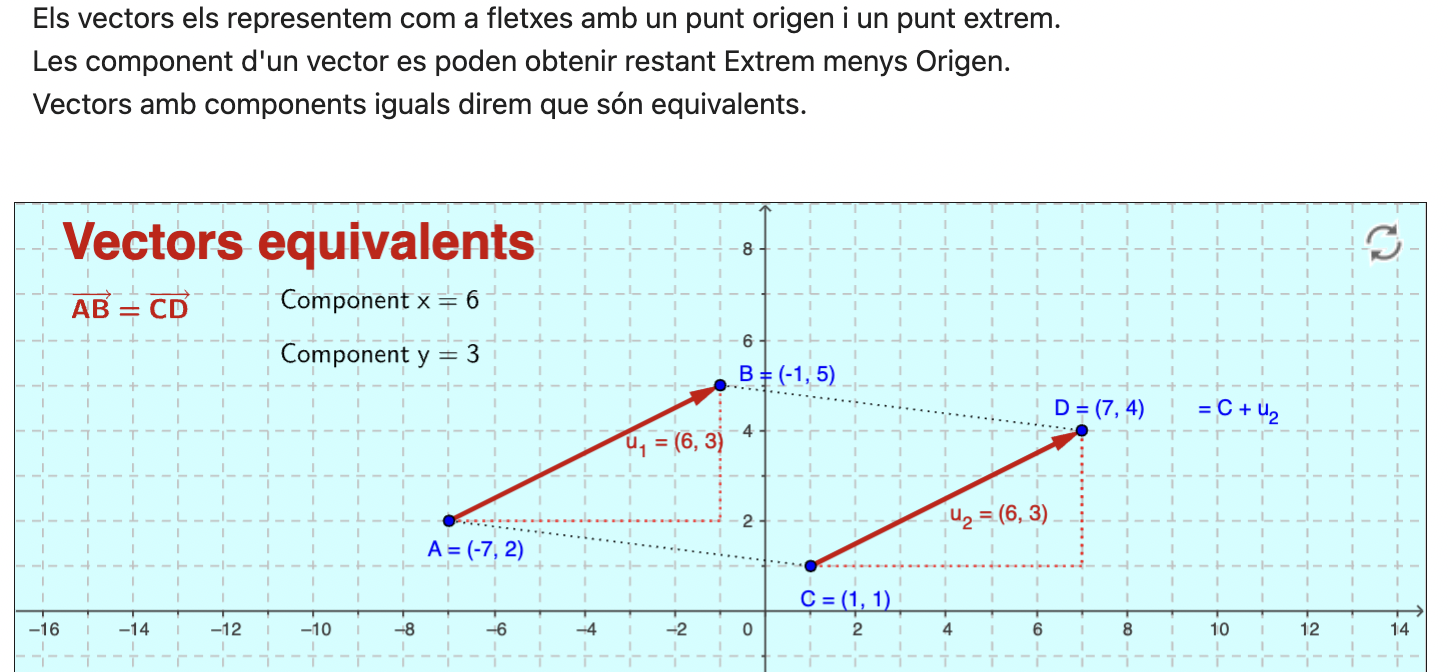
A. Comprensió del concepte i característiques (mòdul, direcció i sentit) dels vectors com a desplaçament entre dos punts. [ESS]

Per treballar els sabers #4.ESP.LS.A, #4.ESP.LS.B i #4.ESP.LS.C tot donant un context proper als alumnes, proposem introduir el concepte de vector com a desplaçament a partir del plànol d’una ciutat ortogonal, com per exemple el de l’Eixample de Barcelona. Si s’aprofita una sortida real, l’activitat encara tindrà més sentit per a l’alumnat.

Font: Educaplay. *Mapa mut de l'Eixample de Barcelona de Pedro Monzo*

Caldrà definir uns eixos de coordenades en els quals la unitat sigui la distància mitjana entre dos carrers paral·lels consecutius, un origen i destacar-hi alguns punts.

L’activitat consisteix a demanar com anirien d’un punt a un altre (d’entre els diversos marcats al plànol) i quina distància real es recorreria. D’aquesta manera, introduïm els vectors, les seves components i les característiques de direcció i sentit. El mòdul del vector s’entén fàcilment com a distància en línia recta entre dos punts i és fàcil conduir-los a adonar-se que, de fet, calcular aquesta distància equival a calcular la hipotenusa del triangle rectangle que té per catets les components del vector desplaçament.

Es pot parlar també de vectors lliures, paral·lels, perpendiculars, etc. En definitiva, pot ser un context sobre el qual anar construint tots els sabers del bloc Localització i representació de 4t d’ESO.

B. Càlcul de les components d’un vector. Determinació del mòdul d’un vector a partir de les components.

Vectors en el pla

Per treballar el saber #4.ESP.LS.B, es poden trobar moltes construccions amb GeoGebra que poden ser ben útils. Un exemple és «Vectors en el pla» de Victòria Oliu.

Es tracta d’una activitat per treballar el càlcul de les components d’un vector i trobar-ne d’equivalents.

Constel·lació d'Orió

Per treballar els sabers #4.ESP.LS.A i #4.ESP.LS.B hi ha el recurs a l’ARC «La constel·lació d’Orió», de Pepe Ródenas, una versió molt clara en paper d’una de les activitats esmentades anteriorment al recurs «Situacions vectorials». Amb els objectius d’identificar punts del pla a partir de les seves coordenades cartesianes, entendre el significat dels vectors (i les seves components) com a desplaçaments entre dos punts del pla i calcular el mòdul d’un vector en 2D emprant el teorema de Pitàgores, es proposa a l’alumnat dibuixar la constel·lació d’Orió sobre una quadrícula a partir de les coordenades cartesianes de les seves estrelles. Després, s’han d’escriure les components dels vectors que connecten determinades parelles d’estrelles i s’ha de calcular a quina distància es troben entre si, fent ús de les components i del teorema de Pitàgores.

C. Ús dels vectors, les seves propietats i les operacions entre ells per resoldre problemes geomètrics senzills. [ESS]

Una proposta per introduir els vectors i resoldre problemes és «Situacions vectorials», de Pere Burgués. Es tracta d’un llibre de GeoGebra que és una adaptació i ampliació de la seqüència presentada per Carles Rodríguez en el seu treball de final de màster «Vectors en el pla a 4t d’ESO: millora i redisseny de la UD».

El llibre consta de diverses parts, totes molt interessants:

«La constel·lació d’Orió» (saber #4.ESP.LS.A). L’objectiu és entendre el significat dels vectors (i les seves components) com a desplaçaments entre dos punts del pla i calcular el mòdul d’un vector.
«El Tour de França» (saber #4.ESP.LS.A). A través del treball amb vectors, es tracta de calcular quina ha estat la distància i el desplaçament total que han fet els ciclistes en una etapa del Tour, entenent la distància com tots els quilòmetres reals que han recorregut els ciclistes tenint en compte el desnivell i el desplaçament com la distància horitzontal que han fet els ciclistes sense tenir en compte el desnivell.
«Producte escalar d’un Vector» (saber #4.ESP.LS.B). Es tracta de veure com canvia un vector quan el multipliquem per un escalar.
«El laberint» (saber #4.ESP.LS.C). A través de la suma de vectors, es tracta de treballar la situació següent. Dues persones s’han trobat enmig d’un laberint i han de trobar la sortida. Han decidit separar-se per trobar la sortida abans, però al cap de poc s’han tornat a trobar en una cruïlla. A partir de les explicacions dels recorreguts que ha fet cadascuna de les persones i encadenant desplaçaments, com la suma de vectors, s’introdueix també la idea de vector oposat i es troba la sortida del laberint.
«Un passeig pel parc» (saber #4.ESP.LS.C). Per treballar desplaçaments i perpendicularitat.
«El mosaic» (saber #4.ESP.LS.C). S’inicia l’activitat fent la proposta següent: com a classe, s’ha tingut la idea de dibuixar un mosaic al pati. Després de moltes idees i debats, el disseny que s’ha triat és el de la imatge que hi ha continuació, en què s’intercalen colors i figures geomètriques:

Font: Pere Burgués. El mosaic

Per poder dibuixar-lo, s’ha dividit el pati en una quadrícula per tenir clar com s’ha de traçar cada línia. El primer repte de l’alumnat és saber com poden determinar el centre exacte del pati per fer la figura central. A través del treball de vectors, distàncies i punts mitjans, l’alumnat resol el repte i arriba a crear el seu propi mosaic.

D. Estudi de les diferents equacions d’una recta. [AMP] #ALG.ID, #ALG.RF

Per treballar el saber #4.ESP.LS.D, podem fer servir «la doble cara del GeoGebra» que mostra un fet molt elemental, però que sovint passa per alt: la relació entre la finestra gràfica i la finestra algebraica. La idea de correspondència entre figures geomètriques i expressions algebraiques pot arribar a ser molt potent.

Amb aquesta idea, tenim el recurs «Investiguem l’equació de la recta» de Jordi Campos, en què s’estudien diferents equacions de la recta tenint en compte les dues finestres del GeoGebra que s’han comentat anteriorment.

E. Determinació dels elements determinants d’una recta (punts, vector director, pendent, angle respecte a l’eix d’abscisses, etc.) donada la seva equació. [AMP]

Per treballar els sabers #4.ESP.LS.D, #4.ESP.LS.E i #4.ESP.LS.F hi ha el recurs amb GeoGebra «Punts, rectes i vectors» de Josep Lluís Cañadilla. En primer lloc, es fa un petit treball amb vectors, introduint el concepte i calculant-ne les components. Tot seguit es mostra com trobar les equacions d’una recta a partir d’un punt i un vector, fet que porta a introduir les equacions paramètriques, l’equació contínua i la general. Tot seguit, es fa un repàs de la potencialitat del GeoGebra a l’hora de treballar amb vectors i rectes i els recursos que ens ofereix:

Crear rectes paral·leles i perpendiculars: Recta(A,f) i Perpendicular(A,f)
Establir la posició relativa (es tallen, són paral·leles o perpendiculars): SónIguals(recta, recta) SónParaleles(recta, recta) SónPerpendiculars(recta, recta)
Trobar el punt de tall de dues rectes: Intersecció(recta, recta)
Mesurar distàncies (d’un punt a una recta o d’una recta a una altra recta): Distància(objecte, objecte)
Mesurar l’angle que formen dos vectors o dues rectes: Angle(recta, recta) o Angle(vector, vector)
Trobar el punt mitjà de dos punts: PuntMitjà(punt,punt)

Finalment, es proposen un seguit de tasques d’aplicació d’allò que s’ha treballat.

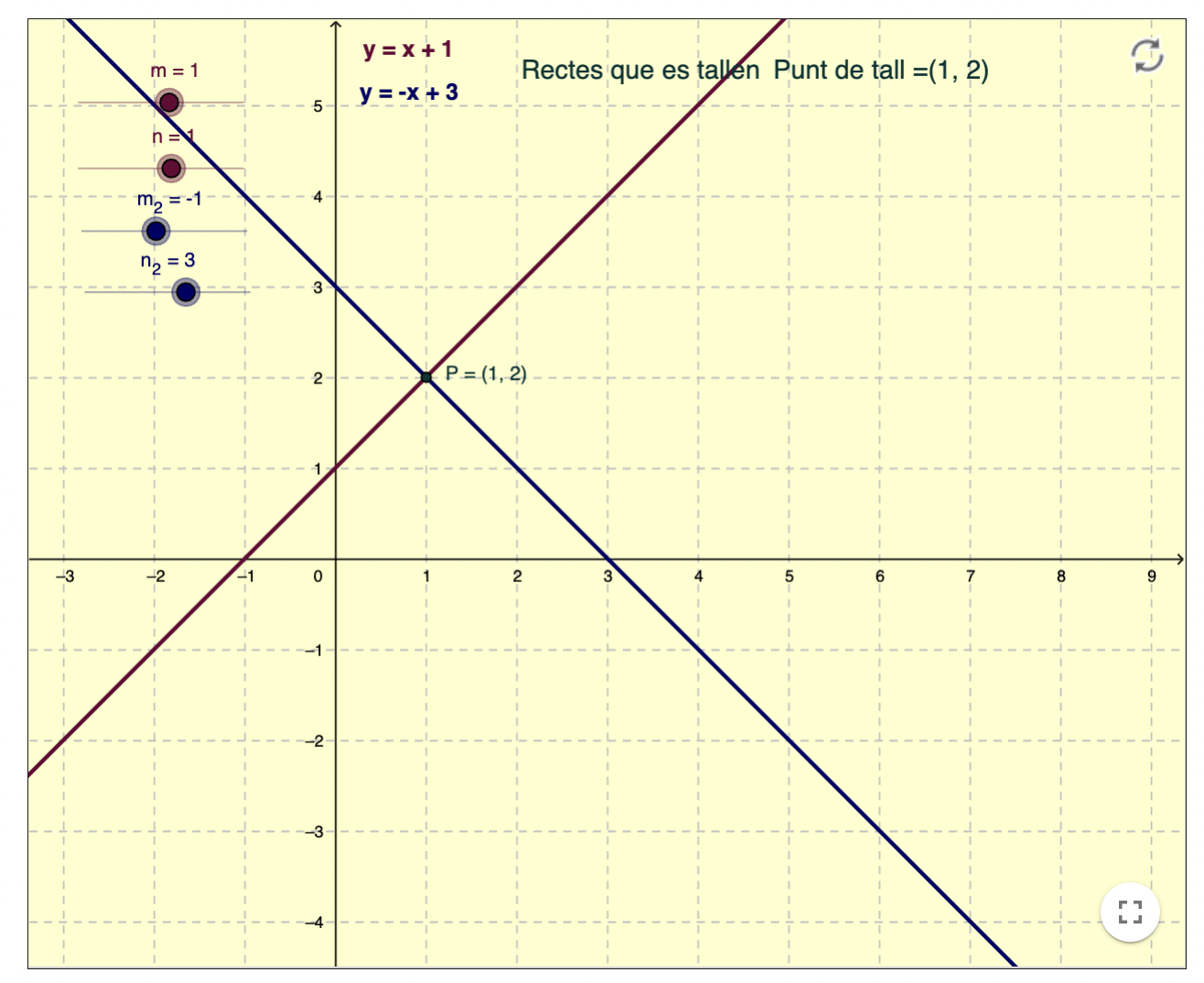
F. Estudi de la posició relativa de dues rectes i determinació del paral·lelisme, la perpendicularitat i el punt de tall, si s’escau. [AMP] #ALG.ID, #ALG.RF

Lots of vector lines!

Per treballar els sabers #4.ESP.LS.D, #4.ESP.LS.E i #4.ESP.LS.F, també hi ha recurs «Lots of vector lines!» del web Underground Mathematics. Es presenten a l’alumnat les dotze equacions de rectes següents:

L’alumnat haurà d’aparellar-les, segons les condicions següents:

Que siguin paral·leles.
Que siguin perpendiculars.
Que tallin l’eix de les x pel mateix punt.
Que tallin l’eix de les y pel mateix punt.
Que passin pel punt (1,5).
Que les dues rectes…

A més de fer les parelles, també hauran de trobar la característica comuna de l’última parella de rectes.

Aquest recurs aprofundeix en el treball amb rectes en forma vectorial i dona l’oportunitat de reflexionar sobre les diferències entre treballar amb unes determinades equacions o unes altres.

De manera similar, hi ha també el recurs «Lots of lines!», en què es tracta de fer exactament el mateix que a l’activitat anterior, però ara amb dotze rectes expressades en diferents formes:

Posició relativa de dues rectes

Per treballar el saber #4.ESP.LS.F hi ha el recurs «Posició relativa de dues rectes» de Victòria Oliu.

L’activitat proposa moure els punts lliscants fins a obtenir parelles de rectes que siguin:

Paral·leles.
Coincidents.
Secants.

Proposa a l’alumnat que observi en cada cas com són els pendents i l’ordenada a l’origen, pregunta com es pot calcular el punt de tall en el cas de les rectes secants i demana dibuixar més exemples a la llibreta i escriure’n les conclusions.

G. Selecció de l’equació de la recta més adequada en funció de la situació que cal resoldre. [AMP]

Rectes i punts notables

Es pot plantejar el treball dels sabers #4.ESP.LS.F i #4.ESP.LS.G a partir de petites investigacions de propietats geomètriques, com per exemple que les tres medianes es tallen en un mateix punt. Amb aquesta idea, es poden trobar molts recursos preparats amb programes de geometria dinàmica. Un d’aquests és «Rectes i punts notables», d’Alba Blasco, fet amb el GeoGebra. La proposta planteja treballar les mediatrius d’un triangle, el circumcentre, les bisectrius, l’incentre, les altures, l’ortocentre, les mitjanes, el baricentre i la recta d’Euler.

Recta d'Euler

Amb la mateixa idea, però menys pautat, hi ha el recurs «Els quatre centres del triangle i la recta d’Euler» de Pep Bujosa i Carlos Giménez Esteban, en què, a partir d’unes definicions donades, s’han de construir el baricentre, l’ortocentre i el circumcentre d’un triangle, i comprovar que estan alineats.

Vector squares

Per treballar els sabers #4.ESP.LS.F i #4.ESP.LS.G també hi ha el recurs «Vector squares», del web Underground Mathematics. Es planteja la situació següent a l’alumnat. Un quadrat està limitat per les equacions:

Font: «Vector squares», del web Underground Mathematics.

Es demana a l’alumnat:

Que comprovi que es tracta realment d’un quadrat, és a dir, que les rectes que formen costats adjacents del quadrat són perpendiculars.
Que trobi la superfície del quadrat.
Que trobi les equacions de les diagonals del quadrat.

En aquest problema, l’alumnat ha d’interpretar i treballar amb equacions vectorials d’una recta, incloent-hi la recerca de punts de tall. El problema també anima els estudiants a establir connexions amb representacions geomètriques i a començar a reconèixer les característiques de les rectes perpendiculars en forma vectorial.

Llicenciat sota la Llicència Creative Commons Reconeixement CompartirIgual 4.0